자료구조와 알고리즘 A+ 기원

1. Motivation 🔎

: 가장 효율적인 알고리즘 = 얼마나 시간이 적게 걸리는가?

• Best Solution = 시간, 공간, 프로그래밍 효율 등 다양한 척도에 의해 정의될 수 있음
  - Time Complexity 시간복잡도: 실행되는데 얼만큼의 시간이 걸리는가?
  - Space Complexity 공간복잡도: 실행되는데 얼만큼의 메모리가 필요한가?

요인

: 프로그램을 실행하는데 걸리는 시간을 결정하는 요소들은?

• Program Size
• Basic Algorithm / Actual Processing
• Memory access speed
• CPU/Processor speed
• the Number of Processors
• Compiler/Linker Optimization

📌 Moore's Law

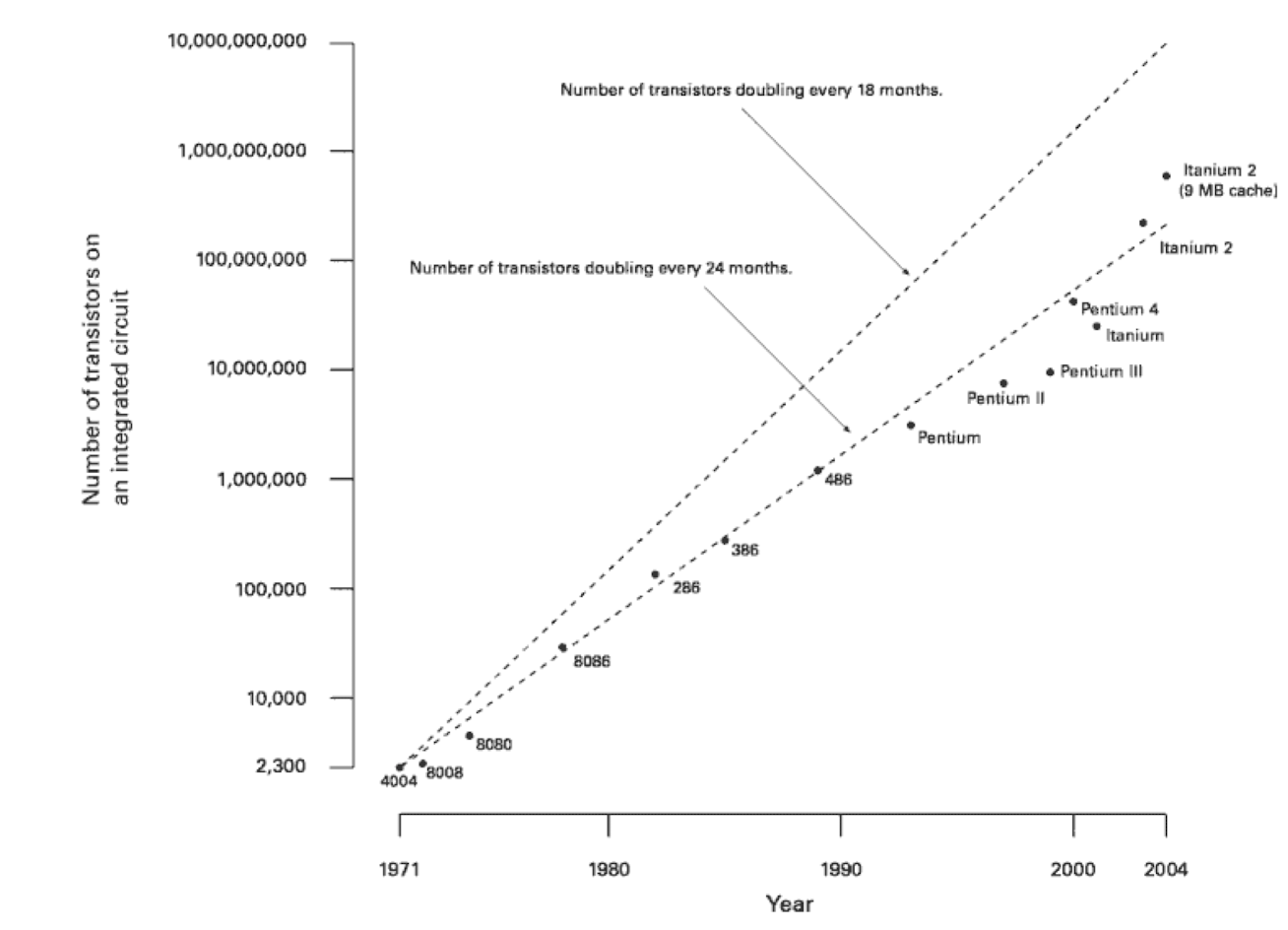
= 시간이 지날수록 컴퓨터의 성능은 더 좋아질 것이다! (경험적 바탕)

2. Measuring an Algorithm Efficiency 🫥

: Growth-rate function = T(n) 전체 시간이 걸리는 데에 가장 중요한 연산의 횟수 n이 늘어날 때마다 해당 알고리즘은 어떻게 되는가?

• 침착하게 n을 하나씩 올리면서 T(n)을 찾아보자!
• 최고차항만 가져가자!

3. Asymptotic Notation 📝

1) 종류

• O Big O 표기법
  : Upper bound
• $\Omega$ Big Omega 표기법
  : Lower bound
• $\theta$ Big Theta 표기법
  : Upper and Lower bound
  

2) Big O 표기법

: 알고리즘 러닝 타임의 상한 계산 = 이것보다는! 적게 걸린다!

$f(n) ∈ O(n^2)$ 에 포함이 되는 친구들

• $n^2$
• $3n^2+2n$
• $3n^2+nlogn$
• $3n$

• 이때 f = growth-rate function
• $3n$ ∈ $n^2$: 틀린 표기법은 아니지만 정보 손실이 있음 (가치 X) -> 최대한 가깝게 설정해주어야 한다!

3) Big $\Omega$ 표기법

: 알고리즘 러닝 타임의 하한 계산 = 최소! 이정도는 걸린다!

$f(n) ∈ \Omega (n^2)$ 에 포함이 되는 친구들

• $n^2$
• $3n^2+2n$
• $3n^2+nlogn$
• $7n^3+5n$

• $7n^3+5n ≥ n^2$: 틀린 표기법은 아니지만 $n^3$이 더 올바름

4) Big $\theta$ 표기법

: 알고리즘 러닝 타임의 상한 & 하한 사이 계산

$\theta (n^2) = O(n^2) ∩ \Omega (n^2)$

= 두 시간 사이 안에는 존재한다!

5) General notation

• Proper notation
  : $T(n) ∈ O(n^2)$
• General notation
  : $T(n) = O(n^2)$ -> ∈ 를 = 으로 고려
• Wrong notation
  : $O(n^2) = T(n)$