[백준] 1009번 : 분산처리

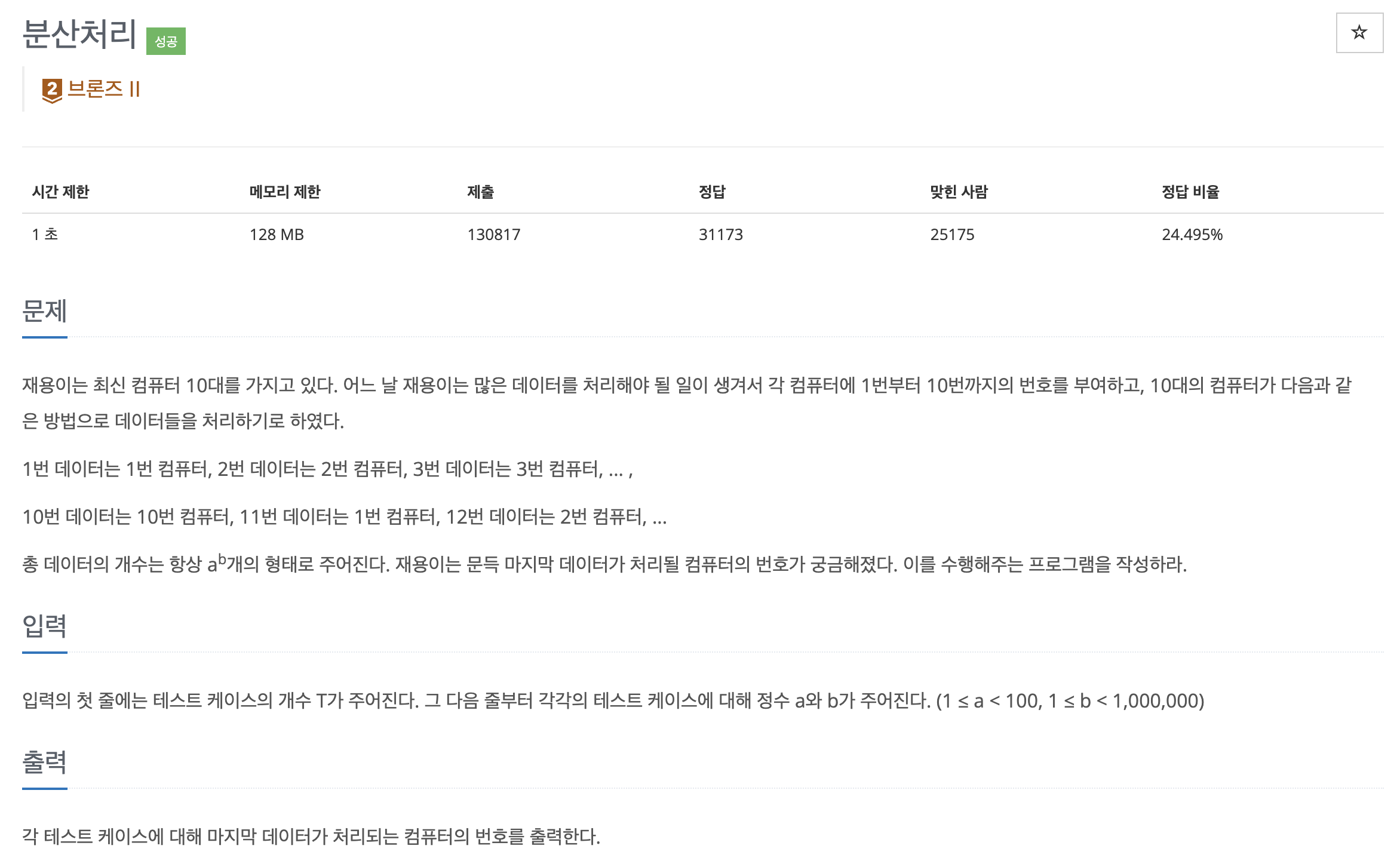
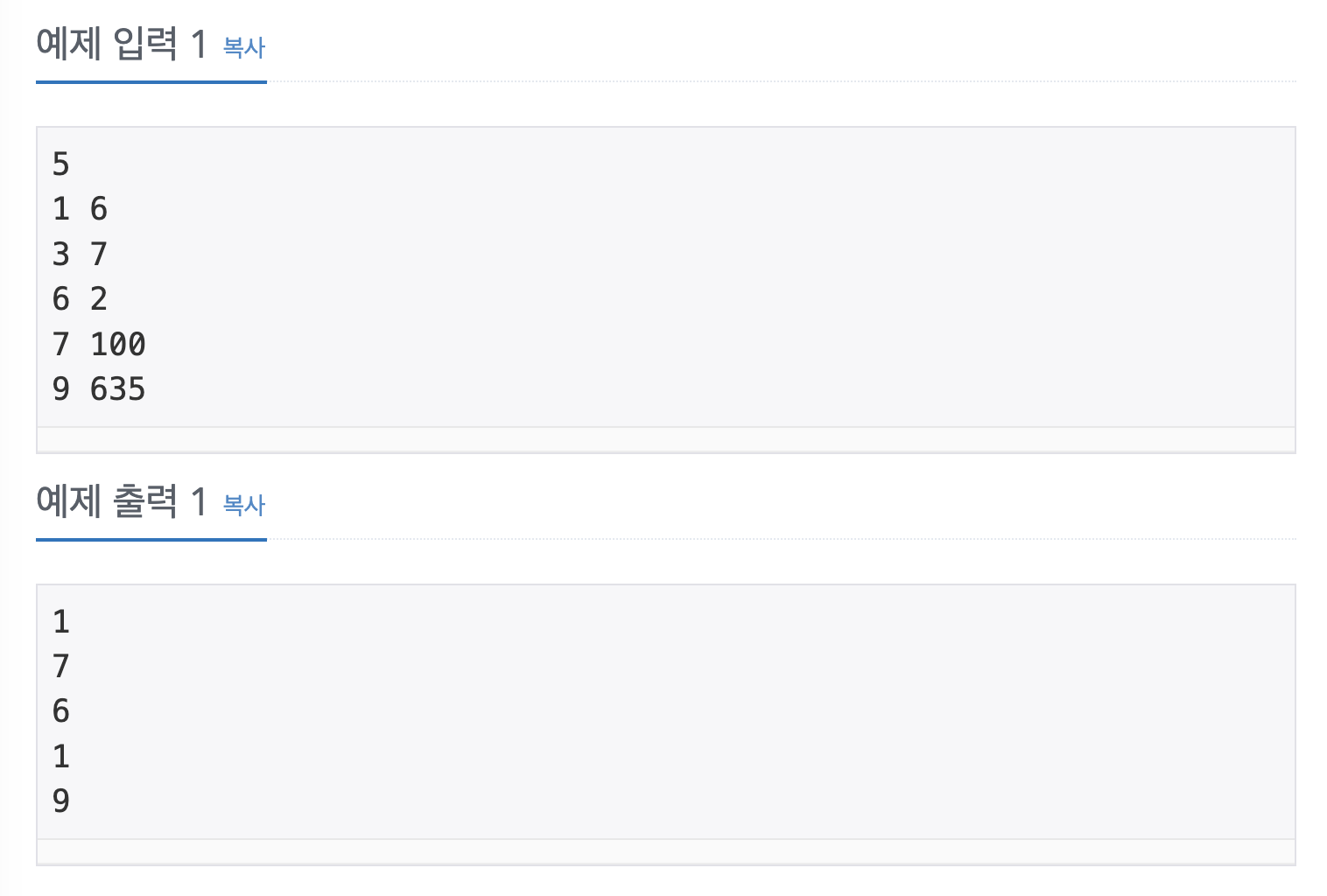
처음에는 a**b % 10 을 이용하여 간단하게 처리할 수 있는 코드라 생각했습니다.
그러나 주어진 a와 b의 범위를 보면 가장 큰 데이터의 갯수가 1001000000 임을 알 수 있습니다.
너무 큰 값으로 인해 계산에 많은 시간이 소요됩니다.

문제의 목적은 $a^b$의 일의 자리 숫자(즉, 10으로 나눈 나머지)를 구하는 것입니다.
이런 경우 전체 거듭제곱을 계산할 필요 없이 패턴을 이용해 효율적으로 해결할 수 있습니다.
일의 자리 숫자는 주기성을 가집니다. 예를 들어:

2의 거듭제곱의 일의 자리: 2, 4, 8, 6, 2, 4, 8, 6, ...
3의 거듭제곱의 일의 자리: 3, 9, 7, 1, 3, 9, 7, 1, ...

간단히 적어보면

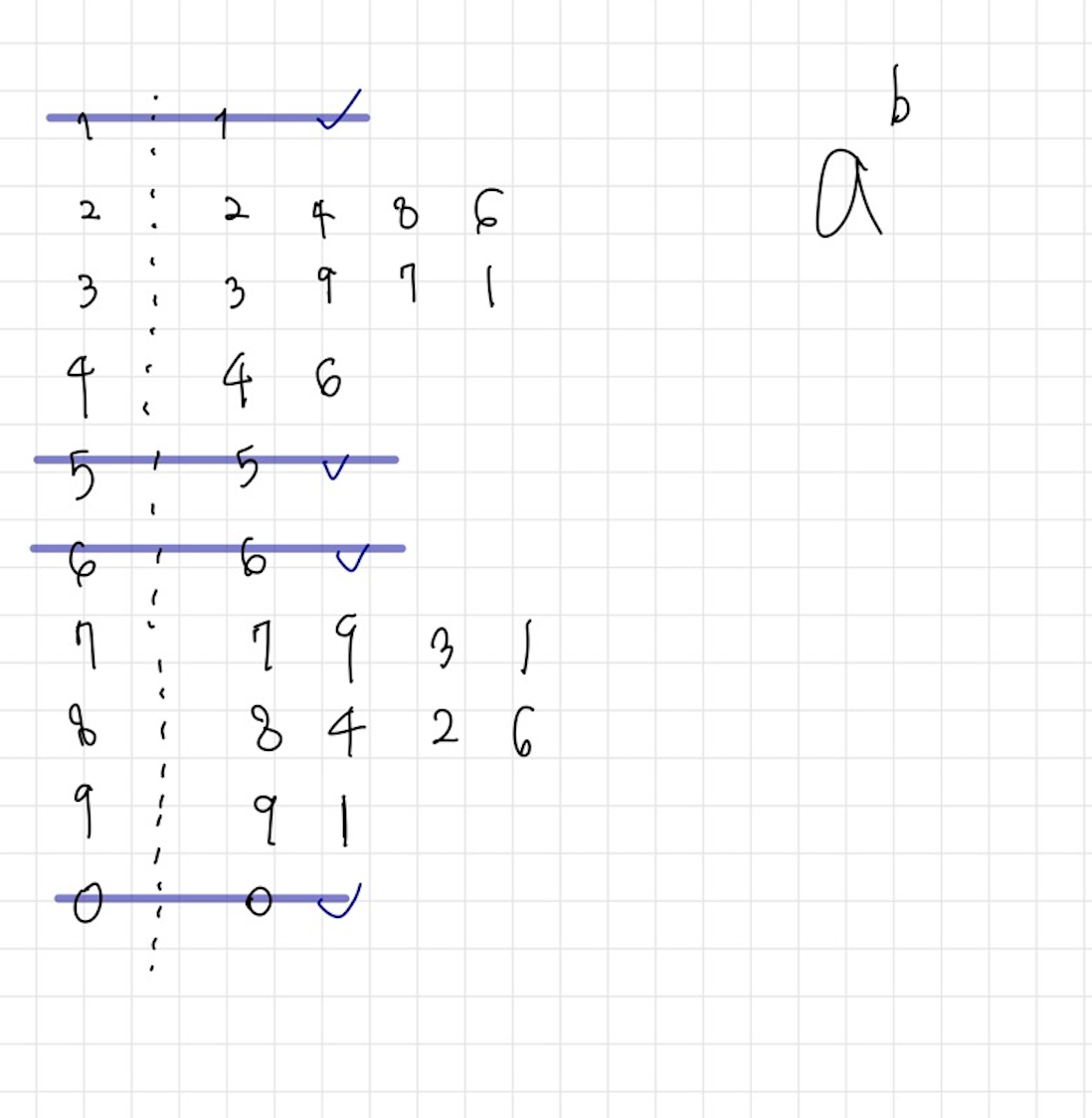
일의 자리가 0부터 9인 경우의 각 주기성을 적어보았습니다.

수학적 특성을 이용해 답을 작성했습니다.

My answer

T = int(input())
for i in range(T):
  a,b = map(int, input().split())


  if a == 0:
    print(0)
  elif a % 10 == 0:
    print(10)
  elif a % 10 == 1:
    print(1)
  elif a % 10 == 5:
    print(5)
  elif a % 10 == 6:
    print(6)

  else:
    if a % 10 == 4:
      if b % 2 == 0:
        print(6)
      else:
        print(4)
    elif a % 10 == 9:
      if b % 2 == 0:
        print(1)
      else:
        print(9)
    elif a % 10 == 2:
      if b % 4 == 0:
        print(6)
      elif b % 4 == 1:
        print(2)
      elif b % 4 == 2:
        print(4)
      elif b % 4 == 3:
        print(8)
    elif  a % 10 == 3:
      if b % 4 == 0:
        print(1)
      elif b % 4 == 1:
        print(3)
      elif b % 4 == 2:
        print(9)
      elif b % 4 == 3:
        print(7)
    elif  a % 10 == 7:
      if b % 4 == 0:
        print(1)
      elif b % 4 == 1:
        print(7)
      elif b % 4 == 2:
        print(9)
      elif b % 4 == 3:
        print(3)
    elif a % 10 == 8:
      if b % 4 == 0:
        print(6)
      elif b % 4 == 1:
        print(8)
      elif b % 4 == 2:
        print(4)
      elif b % 4 == 3:
        print(2)

밑의 답변은 AI에게 부탁해 좀 더 간단한 코드로 작성한 것입니다.

def solve(a, b):
    # 내장 함수 pow()를 사용해 a^b mod 10 계산
    result = pow(a, b, 10)
    # 결과가 0이면 10번 컴퓨터, 아니면 해당 번호 컴퓨터
    return 10 if result == 0 else result

# 테스트 케이스 수 입력
t = int(input())

for _ in range(t):
    a, b = map(int, input().split())
    print(solve(a, b))

Python의 pow() 함수는 세 번째 인자로 모듈러 값을 받을 수 있습니다.
pow(a, b, m)는 a의 b제곱을 m으로 나눈 나머지를 반환합니다.
즉, pow(a, b, m)은 수학적으로 ($a^b$) % m과 동일합니다. 하지만 파이썬의 내장 pow() 함수는 중간 계산 과정에서도 모듈러 연산을 적용하는 최적화된 알고리즘을 사용하기 때문에, 직접 $a^b$를 계산한 후 m으로 나누는 것보다 훨씬 효율적입니다.
특히 b가 매우 큰 경우(이 문제에서는 최대 1,000,000까지), 이런 최적화는 시간 초과를 방지하는 데 중요합니다.