22251번: 빌런 호석

• 빌딩 엘리베이터는 1층부터 N층까지 이용 가능하다.
• 엘리베이터 디스플레이는 K자리 숫자를 표시하며, 숫자는 0으로 시작할 수 있다.
• 각 숫자는 7개의 LED 표시등으로 구성되어 있다.
• 빌런 호석은 LED를 최소 1개, 최대 P개 반전시켜 다른 층수를 표시할 계획이다.
• 현재 엘리베이터가 X층에 있을 때, 호석이 LED를 반전시켜 1층 이상 N층 이하의 다른 유효한 층수를 표시할 수 있는 경우의 수를 구한다.
• 제한: 1 ≤ X ≤ N < 10^K, 1 ≤ K ≤ 6, 1 ≤ P ≤ 42

접근

반전에 필요한 LED 수 구하기

7개의 LED로 구성된 세븐 세그먼트로 숫자가 표시된다.
반전 가능한 LED 수가 제한되어있기 때문에 숫자가 변할 때 필요한 LED 수를 계산해야한다.
예를 들어, 0에서 1로는 4개의 LED가 반전되어야한다.

숫자가 0~9로 제한되어있기 때문에 반전에 필요한 LED 수를 직접 셀 수도 있지만, 인간 오류의 가능성과 시간적 효율이 좋지 않다.
따라서 숫자를 바이너리로 표현한 다음에 변경에 필요한 LED 수를 연산하는 것이 효율적이며, 오류의 가능성도 적다.

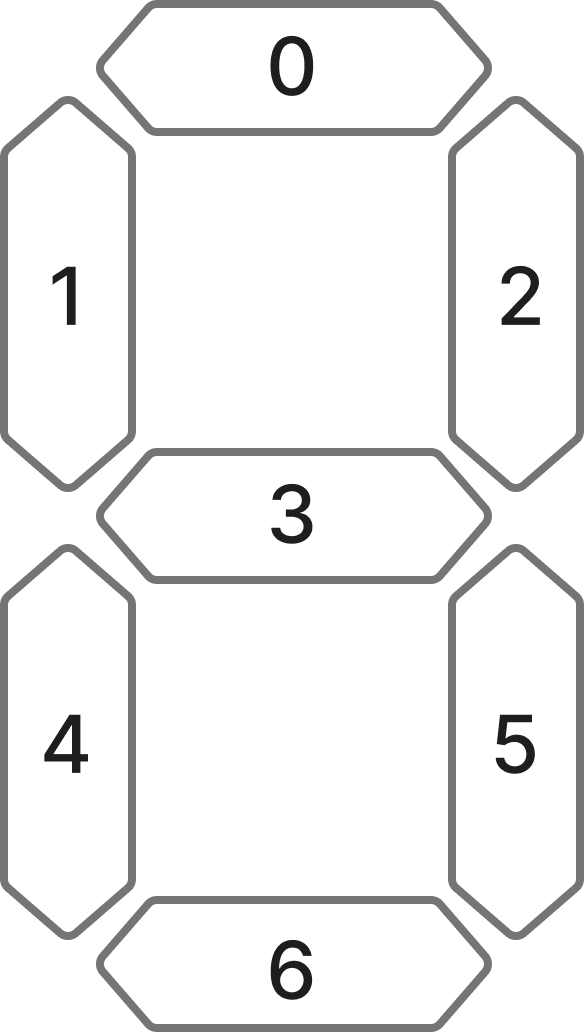
이렇게 각 LED 세그먼트를 0~6번으로 표현했을 때, 0 같은 경우 바이너리로 왼쪽부터 0번 LED로 시작해 0x1110111로 표현할 수 있다.
그리고 각 숫자끼리 XOR 연산을 해서 변경되어야하는 비트만 1로 표시되면 XOR 후 켜진 비트의 개수 = 변경해야할 비트의 수가 된다.

층별로 확인하기

층수의 수가 많지 않고, O(N)로 연산되기 때문에 시작 층으로부터 해당 층으로 변경할 때 필요한 LED 수를 제한된 수와 비교해서 개수를 세어주면 된다.

코드

import java.util.*;
import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        
        input(in);
        solve();   
    }
    
    static int height;
    static int digit;
    static int limit;
    static int floor;
    static int[][] cost;
    static int[] num = {
    	0b1110111, // 0
    	0b0010010, // 1
    	0b1011101, // 2
    	0b1011011, // 3
    	0b0111010, // 4
    	0b1101011, // 5
    	0b1101111, // 6
    	0b1010010, // 7
    	0b1111111, // 8
    	0b1111011, // 9
    };
    static void input(BufferedReader in) throws IOException {
    	StringTokenizer tokens = new StringTokenizer(in.readLine());
    	height = Integer.parseInt(tokens.nextToken());
    	digit = Integer.parseInt(tokens.nextToken());
    	limit = Integer.parseInt(tokens.nextToken());
    	floor = Integer.parseInt(tokens.nextToken());
    	
    	cost = new int[10][10];
    	
    	// 각 숫자끼리 변경에 필요한 LED 수 미리 계산
    	for(int i = 0; i < 10; i++) {
    		for(int j = 0; j < 10; j++) {
    			int from = num[i];
    			int to = num[j];
    			
    			int diff =  Integer.bitCount(from ^ to);
    			cost[i][j] = diff;
    		}
    	}
    }
    
    static void solve() {
    	int cnt = 0;
    	
    	for(int i = 1; i <= height; i++) {
    		if(floor != i && countRequiredLED(floor, i) <= limit) cnt++;
    	}
    	
    	System.out.println(cnt);
    }
    
    static int countRequiredLED(int from, int to) {
    	int sum = 0;
    	for(int i = 0; i < digit; i++) {
    		int digitFrom = from % 10;
    		int digitTo = to % 10;
    		sum += cost[digitFrom][digitTo];
    		from /= 10;
    		to /= 10;
    	}
    	return sum;
    }
}

회고

• 세븐 세그먼트를 비트 연산으로 해결하면 오류를 줄일 수 있고, 일일이 세그먼트를 셀 필요도 없다.