[CS] 보수

보수의 정의는 각 자리의 숫자의 합이 어느 일정한 수가 되도록 하는 수이다. 즉, 현재의 숫자에서 자릿수가 한 단계 올라갈 수 있게 해주는 수이다. 주로 1의 보수와 2의 보수가 대표적으로 쓰인다.

10진수는 10을 기점으로 자릿수를 올린다. 그렇다면 십진법에서 1의 보수는 1이 10이 될 수 있도록 해주는 수, 9이다.

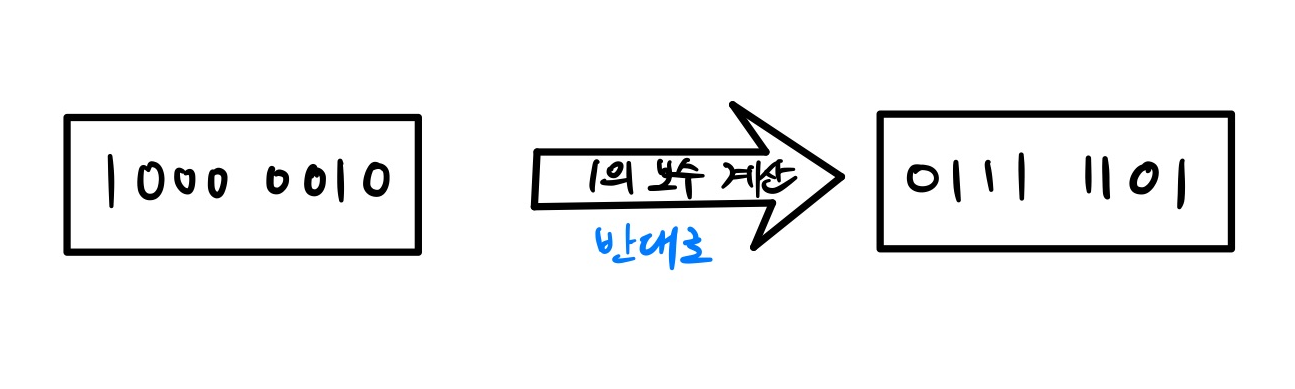
2진법에서는 모든 자리의 수를 1로 만드는 수가 보수이다. 즉, 2진수의 1의 보수는 그 2진수의 반대 (0이면 1, 1이면 0) 라고 생각하면 된다.

보수를 쓰는 이유

왜 이 보충해 주는 수가 필요할까? 그것은 바로 컴퓨터에서는 ‘뺄셈이 없기’ 때문이다. 컴퓨터의 사칙연산은 Adder(가산기)만 이용되기 때문에, A-B의 연산은 불가능하다. 이를 위해 A + (-B) 로 연산 형식을 바꾸어 주어야 하고, 이를 위해 B의 보수인 (-B)를 구하는 과정이 필요하기 때문이다.

1의 보수

이진수에서 0은 1로, 1은 0으로 반대로 바꾸면 1의 보수이다. 2의 보수는 먼저 1의 보수 방식대로 각 자리의 수를 반대로 바꾸고 그곳에 1을 더해야한다.

1의 보수의 문제점

(10진수) 1 → (2진수) 0000 0001
0000 0001에 1의 보수 방식을 통해 -1을 구하면 1111 1110

1 + (-1) = 0 즉, 2진수로 0000 0000이 나와야 한다.
하지만 0000 0001 + 1111 1110 = 1111 1111이 나온다.
1의 보수 방식에서는 0000 0000과 1111 1111을 모두 0으로 취급해버리기 때문이다. 그래서 계산에 오류가 발생할 수 있고, 이런 모호함이 없는 2의 보수 계산법을 이진법에선 주로 사용한다.

2의 보수

2의 보수는 1의 보수를 한 결과에 +1을 더하는 방식으로 이루어진다. 2의 보수 계산법을 통해 아까의 계산을 다시 한 번 해보자.

0000 0001 의 1의 보수는 1111 1110
2의 보수 방식에 따라 1을 더하면 1111 1111

0000 0001 + 1111 1111 를 계산하면 1과 1이 만나는 지점은 2가 되어 자릿수를 올리기에 '1 0000 0000'이 나오지만, 이 맨 앞의 1은 8자리까지 표현할 수 있는 이진법의 범위를 벗어났기 때문에 최종적으로 '0000 0000'이 되며, 모호하지 않은 한가지의 값만 갖는 0이 나오는 것이다.

아래 그림을 통해 계산법을 좀 더 꼼꼼히 익혀보자.

1의 보수 계산은 0은 1로, 1은 0으로 각 자릿수를 반대로 바꾸어 주면 된다.

2의 보수 계산은 1의 보수 계산한 결과에 +1을 해준다.

그럼 이것을 이용한 응용 문제를 스스로 만들어보고 풀어보자.

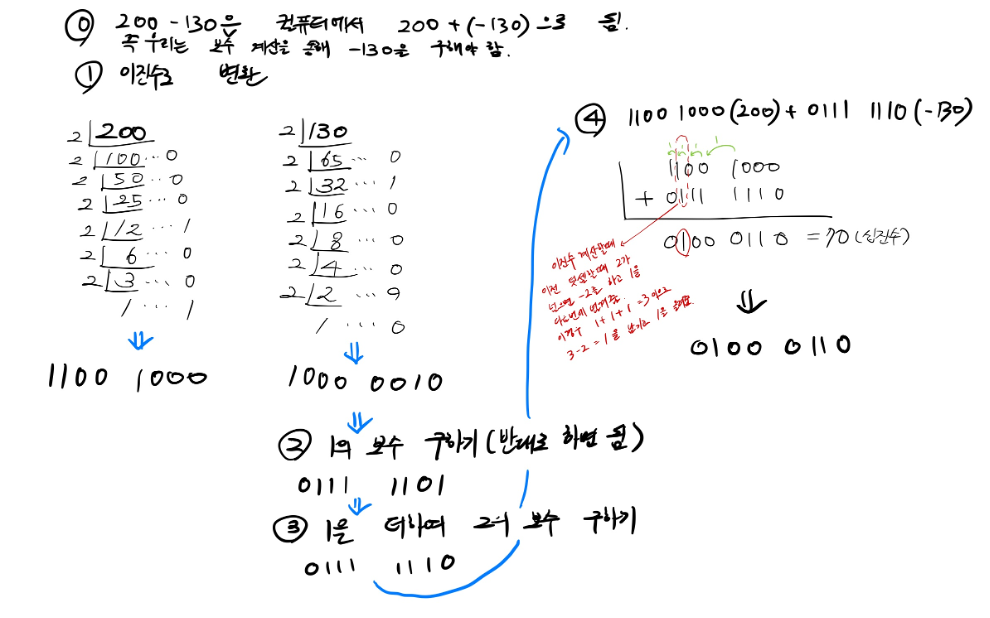
문제) 컴퓨터에서 200-130을 어떻게 처리하는지 2의 보수법을 통해 설명하라

답: 컴퓨터에선 뺄셈이 없기 때문에 A – B의 연산은 A + (-B)로 변환하여 한다고 말한 바 있다. B를 -B로 만드는게 보수를 구하는 과정이고, 결론적으로 우린 200 + (-130)을 하면 되는 과정이다. 200과 -130을 컴퓨터가 이해해야 하니
1. 우선 200 과 130을 각각 2진수로 변환하고
2. 130은 -130이 되어야 하니 2의 보수 계산법을 통해 -130을 구하고,
3.두 수를 더하면 결과가 나온다.

(여기서 참고해야 할 점은 이진수끼리 더하는 과정에서 1과 1이 만나 2가 되면 현재 자리에는 0을 남기고 다음 자릿수로 1을 올린다. 이 1을 올리는 과정은 1+1 이 되었을때 -2를 해주고나서 1을 올리는거다. 아래 그림에서 빨간색 점선 부분은 전 계산에서 1이 올라왔는데, 더해야할 이진수도 둘 다 1 1 이라 총 1+1+1 = 3이 되는데, 여기서 -2를 해주면 1이 남는다. 이 1을 밑에 결과로 남기고 다음 자릿수에 1을 올려주면 된다.)

9의 보수 & 10의 보수

1의 보수와 2의 보수는 주로 2진법에서 쓰이고, 9의 보수와 10의 보수는 10진법에서 사용되는데, 자주 사용하진 않지만 보수를 배우는 김에 간단히 알아보자.

9의 보수는 10진수 각 자리에서 9를 뺀 수이다. 즉 529의 9의보수를 구하면 999-529 = 470이 나온다.

10의 보수는 해당 수의 제일 큰 자리에서 올림한 수에서 해당 수를 빼는 것인데, 529 가 100의 자리 수니까 여기서 올림하면 1000, 1000-529 = 471이 나온다.

하지만 이는 1의 보수와 2의 보수 관계처럼 9의 보수에 +1을 한 결과와 마찬가지이다. 따라서 먼저 9의 보수 계산으로 구한 후 +1을 해주면 된다