[PCCP 기출문제] 2번 / 석유 시추 자바

알고리즘 문제를 풀던 도중 재밌는 문제를 만나 글을 쓰게 되었다.

석유시추 문제 링크

[본 문제는 정확성과 효율성 테스트 각각 점수가 있는 문제입니다.]

세로길이가 n 가로길이가 m인 격자 모양의 땅 속에서 석유가 발견되었습니다. 석유는 여러 덩어리로 나누어 묻혀있습니다. 당신이 시추관을 수직으로 단 하나만 뚫을 수 있을 때, 가장 많은 석유를 뽑을 수 있는 시추관의 위치를 찾으려고 합니다. 시추관은 열 하나를 관통하는 형태여야 하며, 열과 열 사이에 시추관을 뚫을 수 없습니다.

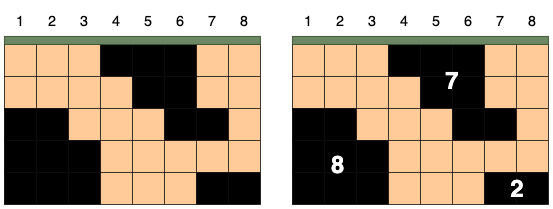
예를 들어 가로가 8, 세로가 5인 격자 모양의 땅 속에 위 그림처럼 석유가 발견되었다고 가정하겠습니다. 상, 하, 좌, 우로 연결된 석유는 하나의 덩어리이며, 석유 덩어리의 크기는 덩어리에 포함된 칸의 수입니다. 그림에서 석유 덩어리의 크기는 왼쪽부터 8, 7, 2입니다.

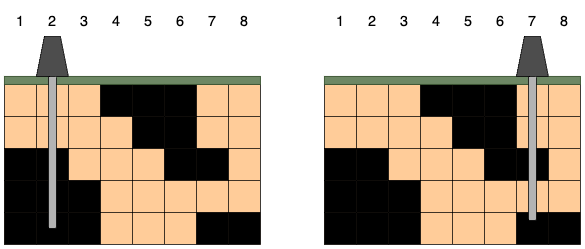
시추관은 위 그림처럼 설치한 위치 아래로 끝까지 뻗어나갑니다. 만약 시추관이 석유 덩어리의 일부를 지나면 해당 덩어리에 속한 모든 석유를 뽑을 수 있습니다. 시추관이 뽑을 수 있는 석유량은 시추관이 지나는 석유 덩어리들의 크기를 모두 합한 값입니다. 시추관을 설치한 위치에 따라 뽑을 수 있는 석유량은 다음과 같습니다.

시추관의 위치 획득한 덩어리 총 석유량
1 [8] 8
2 [8] 8
3 [8] 8
4 [7] 7
5 [7] 7
6 [7] 7
7 [7, 2] 9
8 [2] 2
오른쪽 그림처럼 7번 열에 시추관을 설치하면 크기가 7, 2인 덩어리의 석유를 얻어 뽑을 수 있는 석유량이 9로 가장 많습니다.

석유가 묻힌 땅과 석유 덩어리를 나타내는 2차원 정수 배열 land가 매개변수로 주어집니다. 이때 시추관 하나를 설치해 뽑을 수 있는 가장 많은 석유량을 return 하도록 solution 함수를 완성해 주세요.

제한사항
1 ≤ land의 길이 = 땅의 세로길이 = n ≤ 500
1 ≤ land[i]의 길이 = 땅의 가로길이 = m ≤ 500
land[i][j]는 i+1행 j+1열 땅의 정보를 나타냅니다.
land[i][j]는 0 또는 1입니다.
land[i][j]가 0이면 빈 땅을, 1이면 석유가 있는 땅을 의미합니다.
정확성 테스트 케이스 제한사항
1 ≤ land의 길이 = 땅의 세로길이 = n ≤ 100
1 ≤ land[i]의 길이 = 땅의 가로길이 = m ≤ 100
효율성 테스트 케이스 제한사항
주어진 조건 외 추가 제한사항 없습니다.

문제는 위와 같다.

풀이
문제를 해결하기 위해 먼저 열을 하나씩 탐색하고 land[i][j]==1 이면 bfs를 돌려서 총 갯수를 구했더니 시간초과가 나왔다. 이를 해결하기 위해서 각 석유의 열이 시작하는 점과 끝나는 점을 탐색해서 int[] arr 배열에 넣어주었다. 이렇게 하면 좀 간단하게 푼 것 같아서 포스팅 해본다.

import java.util.*;

class Solution {
    static int[] arr;
    static int dx[] = new int[]{-1,0,1,0};
    static int dy[] = new int[]{0,1,0,-1};
    static boolean[][] v;
    
    public int solution(int[][] land) {
        int answer=0;
        arr = new int[501];
        v = new boolean[land.length][land[0].length];
        for(int j=0;j<land[0].length;j++){
            for(int i=0;i<land.length;i++){
                if(land[i][j]==1){
                    if(!v[i][j]){
                        bfs(land,i,j);
                        
                        
                    }
                }        
            }
        }
        for(int i=0;i<arr.length;i++){
            if(arr[i]!=0)
                answer = Math.max(answer,arr[i]);
        }
        return answer;
    }

    static void bfs(int[][] land,int x,int y){
        Queue<Integer> q = new LinkedList<>();
        q.add(x);
        q.add(y);
        v[x][y]=true;
        int cnt =1;
        int start = y;
        int end = y;
        while(!q.isEmpty()){
            int xx = q.poll();
            int yy = q.poll();
            for(int c=0;c<4;c++){
                int nx = xx+dx[c];
                int ny = yy+dy[c];
                if(nx<0||ny<0||nx>=land.length||ny>=land[0].length) continue;
                if(v[nx][ny]) continue;
                if(land[nx][ny]==0) continue;
                v[nx][ny]=true;
                cnt++;
                q.add(nx);
                q.add(ny);
                start = Math.min(start,ny);
                end = Math.max(end,ny);
            }
        }
        // System.out.println(start+" "+end+" "+cnt);
        for(int i=start;i<=end;i++){
            arr[i]+=cnt;
        }
    }
}