Big-O
Which Code is Best ??
어떤 코드가 좋은 코드일까? 좋은 코드의 조건은 크게 세 가지가 있다.
- Readarable
- Memory : Space Complexity
- Speed : Time Complexity
Big O는 알고리즘 내에서 시간 혹은 공간의 효율성을 따질 때 사용하는 표기법이다. 즉, 인풋값이 무한대로 커졌을 때 나의 알고리즘 효율성이 얼마나 좋느냐를 판별 하기 위해 사용된다.
알고리즘의 정확한 런타임을 나타내는 것은 어렵다. 컴퓨터의 성능 혹은 상황에 따라서 이 런타임은 같은 알고리즘이라도 달라질 수 있다. 그렇기 때문에 시간의 상승률을 패턴으로 표현하는 Big-O 표기법이 중요하다. 명심할 것은 정확한 시간을 측정하는 것이 아닌 대략적인 패턴의 런타임 성장정도(시간이 갈 수록 얼마나 빠르게 증가하는지)를 측정 하는 것이다.
Big-O를 사용하기 위해서 알고리즘에 인풋되는 값이 무엇인지 아는 것이 중요하다. 보통 인풋을 n 이라고 표기한다. 이 n이 커짐과 동시에 그래프가 어떤 모양을 띄는지가 중요하다. 따라서 우리는 알고리즘을 일반화시켜서 전반적인 큰 그림을 봐야한다.
시간복잡도에 영향을 주는 요소들
- Operations (
+,-,*,/) - Comparisons (
<,>,==) - Looping (
for,while) - Outside Function call (
function())
Big-O의 종류
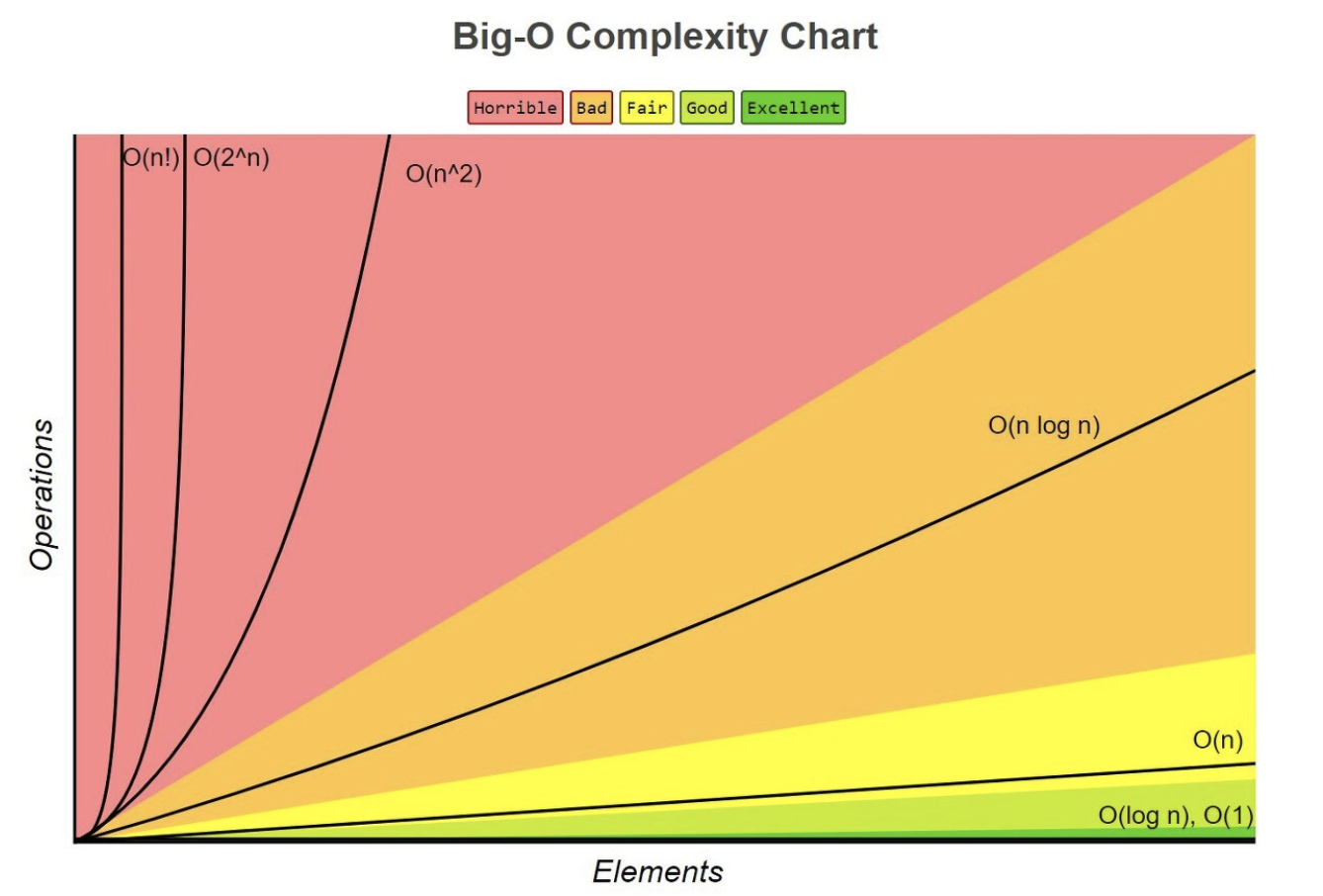
위 이미지는 Big-O 를 그래프로 나타낸 차트이다. 보이는 것과 같이 정확한 시간을 나타내는 것이 아닌, 성장패턴을 그래프로 보여주고 있다. Big-O 표기법에는 총 6가지가 있는데, 그 중에서도 O(1) O(n) O(n^2) 가 제일 많이 사용된다.
O(1) Constant ⭐️
- 반복문이 없다.
- 인풋에 뭘 넣어도 상관 없이 시간이 일정한 상황이다. 즉, 데이터가 어마어마하게 커져도 성능에 영향을 거의 미치지 않는다.
function compressFirstBox(boxes) {
console.log(boxes[0]);
}- box의 갯수에 상관없이 제일 첫 번째 요소만 가져오기 때문에 작업은 한 번만 이루어진다.
O(log N) Logarithmic
- 일반적으로 검색 알고리즘이 정렬된 경우
log n을 갖는다. (Binary Search) - 초반에는 증가하지만 후반에는 거의 수평적으로 간다. 시간이 지날수록 일정하게 증가하기 때문에 인풋의 데이터가 크다면 효율성이 좋다.하지만 전반적인 증가 속도는 갈수록 감소한다.
O(n) Linear ⭐️
forloops,whileloops through n items- x가 증가함에 따라 y도 계속 똑같이 증가하는 그래프이다. 따라서 그래프가 직선(Linear)으로 올라가는 모양이다. 데이터와 시간이 비례하기 때문에 데이터가 10배가 되면 처리시간도 10배가 된다.
const everyone = ['dory', 'bruce', 'marlin', 'nemo', 'gill', 'bloat', 'nigel', 'squirt', 'darla', 'hank'];
findNemo = (array => {
for (let i = 0; i < array.length; i++) {
if (array[i] === 'nemo') {
console.log("Found nemo");
}
}
});
findNemo(everyone);everyone이라는 배열의 길이만큼 콘솔에 문자가 입력된다. 만약에everyone이라는 배열의 길이가 100이라면 정비례하게 100번의 문자가 입력될 것이다.
O(n log(n)) Log Linear
- usually sorting operations
O(n^2) Quadratic ⭐️
- every element in a collection needs to be compared to ever other element.
- loop가 겹쳐져(nested) 있을 때에 사용된다.
- loop 안에 loop가 있을 경우
+가 아닌*가 사용된다. 따라서O(n * n) = O(n^2)이다.
const boxes = ['a','b','c','d','e'];
function logAllPairsOfArray(array) {
for (let i = 0; i < array.length; i++) {
for (let k = 0; k < array.length; k++) {
console.log(array[i], array[j]);
}
}
}
logAllPairsOfArray(boxes);O(2^n) Exponential
- recursive algorithms that solves a problem of size N
O(n!) Factorial
- you are adding a loop for every element
- 아주 아주 비효율적인 Big-O 이다. 보기도 힘들뿐더러 이런 코드를 작성할 일은 없게끔 해야한다.
Big-O의 4가지 규칙
Rule #1. Worst Case
Big-O를 계산할 때는 늘 최악의 상황을 고려해야 한다.
const nemo = ['nemo'];
const everyone = ['dory', 'bruce', 'marlin', 'nemo', 'gill', 'bloat', 'nigel', 'squirt', 'darla', 'hank'];
const large = new Array(10000).fill('nemo');
findNemo = (array => {
for (let i = 0; i < array.length; i++) {
if (array[i] === 'nemo') {
console.log("Found NEMO");
}
}
});
findNemo(everyone);위 예제에서 3번째 인덱스에 있는 nemo를 찾아도 루프는 10번이 돌아간다. nemo를 찾았을 때 loop를 멈추고 싶다면 아래와 같이 작성을 해줘야 시간과 메모리를 낭비할 필요 없이 더 효율적이게 된다.
function findNemo(array) {
for (let i = 0; i < array.length; i++) {
console.log('running')
if (array[i] === 'nemo') {
console.log('Found Nemo!')
break;
}
}
}하지만 이 함수에 들어가는 n 즉 everyone 배열을 보자. 지금은 nemo가 3번째 인덱스에 있지만, 최악의 상황에는 어떻게 될까?? 최악의 상황에는 nemo가 배열의 제일 마지막 인덱스에 위치하고 있을 것이다. 배열의 제일 마지막 인덱스까지 가기 위해서 우리는 계속 loop를 돌아야한다. (참고로 nemo가 제일 첫 인덱스에 위치하고 있으면 시간복잡도는 O(1)이 된다.) 따라서 n과 내가 찾아야 하는 요소의 위치나 상황등을 고려해 최악의 시간 복잡도가 어떻게 되는지 항상 알아보아야 한다.
Rule #2. Remove Constants
Big-O는 정확한 수치를 나타내는 것이 아니기 때문에 중요하지 않은 항과 상수, 계수를 제거한 표기법(점근적 표기법)을 사용한다.
f(x) = 2x^3 + 3x + 1이 함수에 들어가는 n이 5면 값을 266 이 될것이다.
100일때는 2,000,301 이고 10000 이면 훨씬 숫자가 커진다. n의 숫자가 늘어날수록 3x + 1 은 의미가 없어지고 우리에게 중요한 것은 2x^3이다. 이를 Big-O로 나타내면
- 2O(n^3)
- O(n^3)
이렇게 두가지 방식으로 나타낼 수 있으나, 2번 표기법이 더 좋다.
function foo (items) {
console.log(items[0])
let middleIndex = Math.floor(items.length / 2) //--> O(n/2)
let index = 0;
while (index < middleIndex) {
console.log(items[index])
index++;
}
for (let i = 0; i < 100; i++) {
console.log('hi')
}
}
foo();각 코드의 시간 복잡도를 더하면 O(1 + n/2 + 100) 이 될 것이다. 하지만 중요하지 않은 것들을 제외하면 O(n/2) 가 남지만 여기에서 2를 나누는 것도 n에 큰 영향을 미치지 않기 때문에 결과적으로 O(n) 이 된다.
function compressBoxTwice(boxes) {
boxes.forEach(function (boxes) {
console.log(boxes);
})
boxes.forEach(function (boxes) {
console.log(boxes);
})
}
compressBoxTwice();위 예제에서도 forEach라는 loop가 두 번 있기 때문에 O(n + n) = O(2n) 이지만 점근적 표기법을 사용해 결과적으로 O(n) 이 남는다.
Rule #3. Different terms for inputs
각 코드에서 사용되는 n 이 같은지 아닌지 판별해야한다.
function compressBoxTwice(boxes, boxes2) {
boxes.forEach(function (boxes) {
console.log(boxes);
})
boxes2.forEach(function (boxes) {
console.log(boxes);
})
}
compressBoxTwice();forEach메서드가 두 번 사용되었기 때문에 O(n) 이라고 판단하기 쉽다. 하지만 두 loop에서 사용된 인자는 다르다. 첫 번째 forEach는 첫 번째 매개변수의 크기에 따라서 다르지만, 두 번째 forEach는 두 번째 매개변수에 따라서 달라진다. 따라서 이 함수의 Big-O는 O(a + b) 이다. 만약에 looping 되는게 두 개라면 서로 다른 요소를 n으로 가져오는지 확인해 보아야 한다.
그럼 만약 두 번째 loop가 첫 번째 loop 안으로 들어가 nested loop가 되면 어떻게 될까?
function compressBoxTwice(boxes, boxes2) {
boxes.forEach(function (boxes) {
boxes2.forEach(function (boxes) {
console.log(boxes);
})
})
}
compressBoxTwice();loop가 nested 되면 시간복잡도는 + 가 아닌 *이 된다고 했다. 따라서 각 forEach가 다른 인자를 n으로 사용했기 때문에 Big-O는 O(a * b) 가 된다.
Rule #4. Drop Non Dominants
알고리즘에 큰 영향을 미치지 않는 애들은 모두 삭제시켜야한다. 위에서 말했듯이 Big-O 표기법은 점근적 표기법을 사용하기 때문에 영향력이 미미한 상수, 계수, 항 등은 모두 삭제하는게 좋다고 했다. 그럼 만약 O(n + n^2) 처럼 n이 여러개 들어왔다면?
function printThenPairSums(numbers) {
console.log('these are the numbers')
numbers.forEach(function (number) {
console.log(number);
})
console.log('and these are their sums')
numbers.forEach(function (firstNumber) {
numbers.forEach(function (secondNumber) {
console.log(firstNumber + secondNumber)
})
})
}
logAllPairsOfArray([1, 2, 3, 4, 5]);위 에제의 Big-O는 O(n + n^2) 이다. 하지만 여기서 n 보다 n^2가 더 중요하기 때문에 (시간복잡도에 더 큰 영향을 미치기 때문에) n은 삭제가 되어서 O(n^2) 가 된다.
공간복잡도 : Space Complexity
공간복잡도에 대해서 이야기 할 때 대표적으로 두 가지를 알아보아야 한다.
- heap
- stack
간단히 말하자면 heap은 변수들이 저장 되는 곳, stack 은 함수가 호출되었을 때 사용 되는 메모리 공간이라고 생각하면 된다.
function boo(n) {
for (let i = 0; i < n.length; i++) {
console.log('hello')
}
}
boo([1, 2, 3, 4, 5])위 함수의 시간복잡도는 loop가 사용되었기 때문에 O(n) 이다. 그럼 공간복잡도는 어떨까? 공간복잡도를 계산 할 때 고려해야 할 것은 "추가적인 공간이 사용 되는지 아닌지" 이다. 위 함수에서는 n의 길이가 어떻든간에 함수 내부에서 그 배열 자체를 컨트롤 하는 것이 아니기 때문에 (배열에 변화를 주지 않기 때문에) 공간복잡도는 O(1) 이다.
TIP : 배열의 사이즈를 늘리거나, 새로운 배열을 만들지 않고 원 배열 내에서 요소들에게 변화를 주는 것을 In Place 라고 한다.
그럼 아래 함수의 공간복잡도는 무엇일까?
function arrayFunc(n) {
let hiArray = [];
for (let i = 0; i < n; i++) {
hiArray[i] = 'hi';
}
return hiArray;
}
arrayFunc(6)이 함수의 시간복잡도 역시 O(n) 이다. 공간복잡도를 계산 할때 추가적인 공간이 사용되었는지를 봐야 한다고 했다. 함수 내에 hiArray 라는 새로운 배열이 추가가 되었다!!!!!! 그럼 n 의 크기에 따라서 hiArray의 길이가 좌지우지된다. 따라서 공간복잡도는 O(n) 이다.
시간복잡도에 영향을 끼치는 요소들은 아래와 같다.
- Variables
- Data Structures
- Function Call
- Allocations
