Data Structure | Hash Table

간단한 인덱스 기반 데이터 구조, 예를 들면 배열을 사용할 때 원하는 값을 찾기 위해 우리는 배열을 loop시켜 한쪽 끝부터 다른 쪽 끝까지 탐색을 시킨다. 만약 배열 안의 요소의 갯수가 많아지면 많아질수록 성능은 저하될 수 밖에 없다. 물론 데이터에 더 빠르게 접근하기 위해 이진검색을 사용하기도 한다. 하지만 만약 중간에 요소를 삽입해야 한다면 삽입된 인덱스를 제외한 기존 요소들의 인덱스를 이동시켜야 하기 때문에 성능이 더 저하될 위험이 있다.
Hash Table
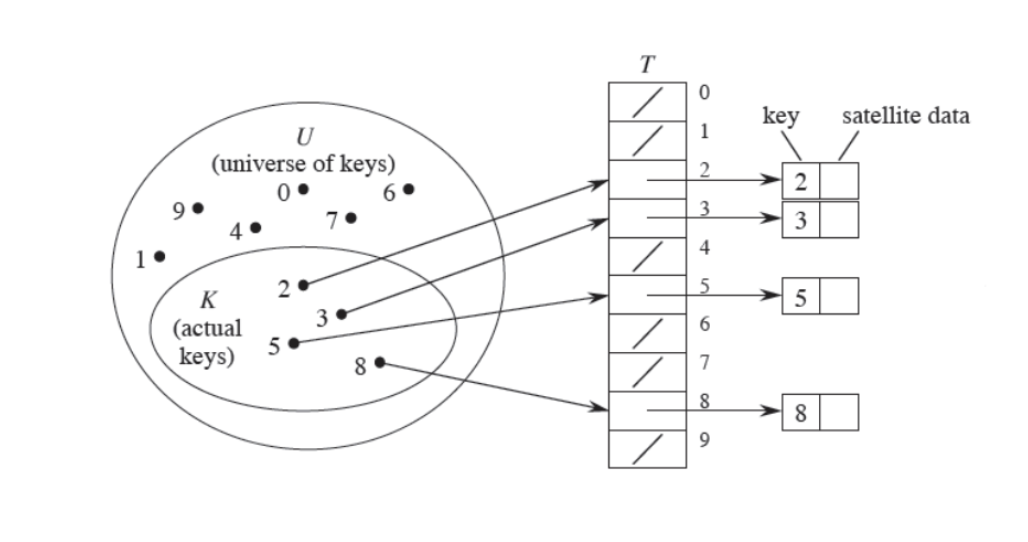
해시 테이블은 대표적인 객체형 자료구조 중 하나이다. 해시 테이블은 해시 함수를 사용하여 키값을 데이터 공간의 구조로 변환하고, 키 값에 대응하는 데이터를 넣는 (key와 value가 쌍을 이룬 형태로) 자료구조형을 말한다. JavaScript에서 사용하는 객체도 해시 테이블의 자료구조의 종류 중 하나이다.
해시 테이블에서는, key 를 hash function 에 넣어서 나온 결과물이 주솟값이 되고, 그 주솟값에 value 를 저장 한 후 참조한다. 해시 테이블은 어느정도 메모리를 확보 해 놓고 해시 함수에서 나온 값을 랜덤하게 자리에 꽂아 넣는 형태인데, 자바스크립트에서는 자체적으로 공간을 확보해 놓는다는 개념이 없다. 따라서 빈 배열이나 빈 객체를 해시 테이블처럼 유사하게 사용한다.
해시 테이블은 중복 데이터를 찾아내기 쉽고, 빠른 탐색과 삽입 및 삭제가 가능하다. 단순 리스트에 저장된 데이터는 중복된 데이터를 찾기 위해서 계속 탐색을 반복해야 하기 때문에 성능상 좋지 않다. 하지만 해시 테이블에 저장하면 데이터가 있는지 순간적으로 알려주기 때문에 중복 확인하는 것이 매우 쉬워진다.
해시 테이블이 엄청나게 좋은 스펙처럼 보이지만 무조건적으로 완벽하다고는 할 수 없다. 만약 저장하고자 하는 자료에 순서가 있을 때는 해시 테이블을 사용하는게 적합하지 않다.(랜덤하게 자리 배정을 하기 때문에) 또한 해시 테이블은 어느정도 공간을 확보하고 시작해야 하기 때문에 쓸모없는 메모리가 낭비 될 수 있다. 제일 중요한 점은 모든 과정에서 해시 함수에 의존하기 때문에 만약 해시 함수가 좋지 않으면 해쉬 테이블 전체에 악영향을 끼친다.
Hash function ?
해시함수는 다양한 길이를 가지고 있는key 를 일정한 길이를 가지는 hash 로 바꿔주어 저장소를 효율적으로 운영 할 수 있도록 도와준다.
hashing 한다 라는 말의 뜻은 인풋(key)을 받아 어떤 함수(hash function)에 집어 넣어서 고정된 자릿수를 가진, 즉 암호화된 결과물을 반환시키는 것 이라고 이해하면 쉽다.
따라서 인풋에 배열이 들어오던, 문자열이 들어오던, 어떤 종류의 데이터가 들어와도 해시함수를 통해서 암호화된 타입의 결과물이 반환되기 때문에 해시 테이블의 시간복잡도는 모두 해시함수에 달려있다고 봐도 무방하다.
그렇다면 해시함수가 꼭 갖추어야 할 조건은 무엇인가?
- 맵핑이 되었을 때 확보된 메모리 공간에 골고루 넣어 줄 수 있어야 한다. (분포가 잘 되어야 함)
만약 한쪽으로 데이터가 쏠리게 되면 충돌이 자주 발생한다.
- 인풋이 나중에 들어오더라도 항상 동일한 아웃풋을 내보내야 한다.
해시함수를 사용할 때마다 다른 결과가 나온다면 해시테이블을 사용할 수 없을 것이다.
- 해시함수 자체적으로 시간 복잡도가 좋아야 한다.
해시함수의 성능은 해시 테이블의 성능과 직접적인 연관이 있다.
Hash Table Collisions
해시 테이블은 충돌이 발생하기 전까지는 아주 성능이 뛰어난 자료구조형이다. 하지만 해쉬 함수를 거쳐서 다른 키를 넣었는데 같은 주솟값이 나오는 경우가 있다. 이럴 때 hash collision (충돌)이 일어난다. 좋은 해시 함수를 사용하게 되면 충돌이 발생할 확률이 낮아지지만 많은 양의 데이터를 처리하다보면 충돌이 불가피하게 생길 수 밖에 없다. 그럼 충돌을 해결할 방법은 무엇인가?
1. 같은 주솟값을 가진 아이들을 Linked list (연결리스트) 구조로 쭈욱 연결지어준다.
하지만 이 방법의 단점은 연결리스트의 길이가 길어질수록 해시테이블의 성능이 매우 낮아진다는 것이다. 같은 주솟값에서 한 요소를 찾기 위해서 모든 연결리스트 내의 요소를 탐색해야 하기 떄문이다.
2. Linear probing (선형탐사) 방법이다.
선형탐사는 충돌이 발생한 지점의 다음 방부터 탐색하여 빈 방이 있으면 그 공간에 데이터를 집어넣는 방법이다. 만약 끝까지 탐색했는데 빈 공간이 없다면 다시 처음으로 돌아와 검사한다. 하지만 이또한 주변에 빈 방이 없다면 모든 방을 탐색해야 한다는 단점이 있다.
3. 충돌을 방지하기 위해서는 넉넉한 메모리 공간을 확보해 hash 의 중복을 최소한으로 시키는 방법이 있다.
Load Factor
해시 테이블에서 Load Factor (사용률)이란 해시 테이블의 공간을 얼마나 사용하고 있는지를 수식화 시킨것이다. 쉽게 말하면 한 버킷에 평균 몇개의 키가 맵핑되는지를 나타내는 수치이다. 보통 1:1 방식의 Directed-address Table의 사용률은 1 이하이며 1보다 클 경우 해시 충돌이 발생할 수 있다.
일반적으로 사용률이 0.7 이상으로 커지면 해시 테이블을 리사이징 하는데, 대략 두 배 정도의 크기로 배열을 만든다. 리사이징이 완료되면 해시 함수를 이용해 기존 테이블에 있는 데이터를 새로운 해시 테이블에 다시 저장해야 한다. 이 과정은 시간이 매우 오래 걸리기 때문에 리사이징을 자주 하는 것은 좋지 않다.
Big O
-
충돌이 일어나지 않았을 때를 가장하면 해시테이블의 시간복잡도는 O(1) 이다.
데이터를 추가 할 때 해시 함수에 키 값을 넣어 주소를 알아낸 후 해당 주소에 데이터를 삽입하면 되기 때문에 O(1)로 표기 할 수 있다. 검색과 삭제도 마찬가지이다. 모두 해시 함수를 통해 주솟값을 알아낼 수 있기 때문에 어떤 키 값을 넣어도 항상 똑같은 시간이 걸린다. -
하지만 최악의 경우 해시테이블의 시간복잡도는 O(n) 이다.
만약 해시 테이블이 충돌이 일어나게 되면, 해시테이블은 같은 주솟값을 가진 아이들을 연결구조 형식으로 이어준다고 했다. 이 연결구조 방식이 길어지면 연결리스트 내의 요소를 계속 탐색해야 하기 때문에 시간복잡도는 O(n)이다.
Map / Set
자바스크립트에서 해쉬 테이블은 Object가 대표적이지만 ES6 이후에 Map 과 Set 이 추가 되었다.
-
Map
자바스크립트의 객체에서 key는 언제나 문자열만 가능하지만 Map에서의 key는 함수, 숫자, 배열같은 타입이 들어오는게 가능하다. 또한 객체는 정렬되지 않은 반면에 Map은 정렬화하는게 가능하다. -
Set
Map과 유사하지만 메모리 공간에 value를 저장하지 않고 key만 저장한다.
정리
전화번호부에서 전화번호를 색인 할 때 가장 빠른 방법인 O(1)로 찾는 방법이 해시테이블이다. 해시함수에 데이터를 넣어서 고유한 키를 생성하고, 이 고유 키를 방 번호 삼아 전화번호부의 데이터를 집어넣는다. 만약 김땡땡의 전화번호를 알고 싶다면 김땡땡을 해시함수에 넣어 방 번호를 확인하면 된다.
이 해시함수는 늘 동일한 인풋이 들어갔을 때 동일한 아웃풋을 내야 하고, 맵핑 되었을 때 데이터가 골고루 배치되어야 한다. 만약 한쪽으로 데이터가 쏠리게 되면 충돌 발생 확률이 매우 높아진다.
해시테이블은 중복 데이터를 찾아내기가 쉽고, 색인 삽입 삭제 속도가 모두 빠르지만 공간 효율성이 낮다는 단점을 갖고 있다. 또 만약 정렬된 데이터를 처리해야 한다면 해시테이블은 랜덤하게 자리배치를 하기 때문에 적합하지 않다.
해시테이블은 기본적으로 해시함수에 의존성이 높기 때문에 해시 함수의 알고리즘에 따라 성능과 효율이 크게 갈릴 수 있다. 이는 충돌이 일어났을 때 더 극대화 될 수 있는데 충돌은 링크드리스트 방식이나 선형탐사 방식으로 해결 할 수 있다. (물론 둘도 단점이 있지만)
해시 테이블은 할당된 공간 대비 저장된 데이터수를 가지고 Load Factor(사용률)을 측정 할 수 있는데, 대게 이 로드팩터가 0.7 이상으로 커지면 해시 테이블을 2배정도로 리사이징 한다. 하지만 이 리사이징 과정이 비용이 매우 크다.
해시 테이블의 실제 사용 예로는 전화번호부, 비트코인, DNS가 도메인을 ip로 변환 할 때를 들 수 있다.
