[Algorithm] What is the Graph?

What is a Graph?

A graph is a data structure made up of vertices and edges. To be precise, it can be seen as an organization chart that expresses the relationship between vertices. In that sense, a tree is a kind of graph. However, unlike a tree, a graph may or may not have an edge at each vertex, and there is no concept of a root node, parents, and children. A graph can also be understood as a network model, a flexible way to represent objects and their relationships to them. Various examples from real life can be graphed. Representatively, there are subway routes and roads in the city center. Since there are many ways to use this method, the problem can be presented in a variety of ways. Graphs are used a lot in algorithms. In particular, you should be familiar with DFS and BFS, which are graph traversal methods.

Terms used in graphs.

Vertices: Also called nodes, vertices store data. (0, 1, 2, 3)
Edge: Also called arcs, it represents the relationship between nodes.
Adjacent vertex: A vertex connected by an edge from above (vertex 0 and vertex 1 are adjacent vertices).
Simple-path: A path that does not have repeated vertices and does not cross the same edge.
Degree: the number of vertices adjacent to a vertex in an undirected graph (vertex 0 has degree 3)
Out-Degree: A term used in directed graphs, which refers to the number of edges going out from a node.
In-Degree: A term used in directed graphs, which refers to the number of edges coming from external nodes.

How to implement a graph.

There are two methods of implementing graphs: adjacency matrix and adjacency list. The two implementations have their respective advantages and disadvantages, but most of them use the adjacency list format.

Adjacency Matrix

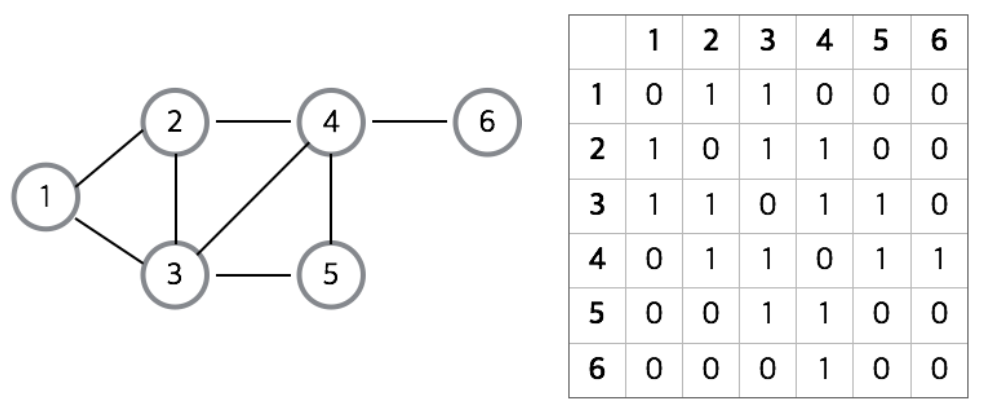
An adjacency matrix is a two-dimensional array of nodes in a graph. For the shape of the completed array, add 1 if other nodes are adjacent vertices to the nodes connecting the vertices of 1, 2, 3, 4, 5, and 6, or 0 otherwise.

Pros

1. Since the edge information of all vertices is contained in a 2D array, it is possible to retrieve the connection information of two points by checking the location of the array with O(1) time complexity.

2. Relatively easy to implement.

Cons

1. It takes O(n²) time complexity because edge information must be substituted for all vertices.

2. Since a two-dimensional array is required unconditionally, more space than necessary is wasted.

Adjacency List

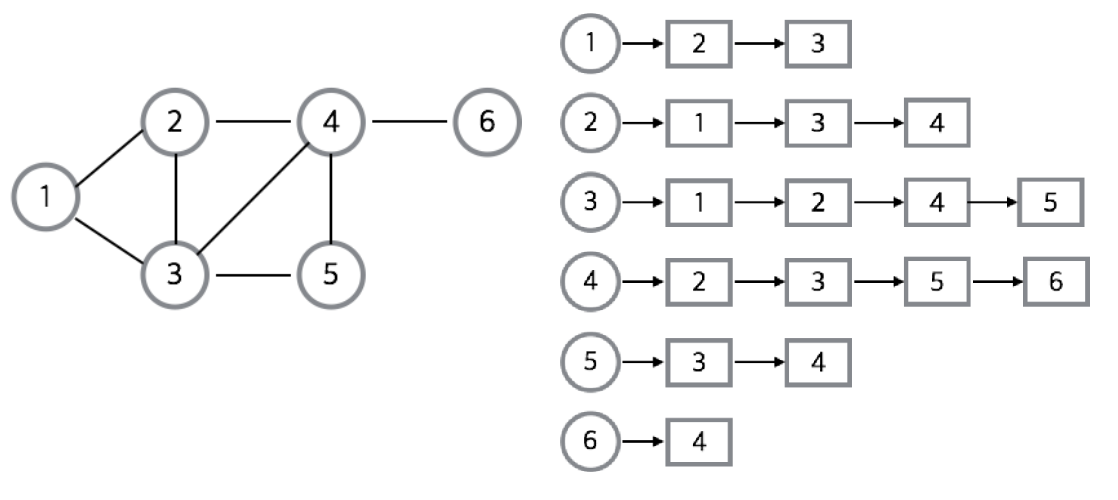
An adjacency list is a list of nodes in a graph. It is mainly implemented by creating a list array of vertices and setting the relationship.

Pros

1. It takes O(n) time to search the connection information of vertices. (n: number of edges)

2. Less space is wasted because it uses only as much space as necessary.

Cons

1. It takes a long time compared to the adjacency matrix to check if certain two points are connected. (Search speed is slower than array)

2. Relatively difficult to implement.

Different types of graphs

Graphs are divided into several types according to the characteristics implemented. Typical types of graphs are as follows.

Undirected graph

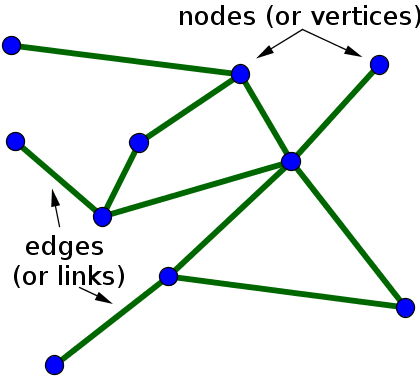
An undirected graph is a graph in which the edge connecting two vertices has no direction.

Directed graph

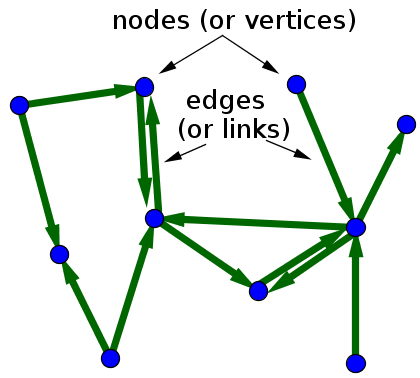
A directed graph is a graph in which the edge connecting two vertices has a direction. You can only move in the direction of an edge.

Weighted graph

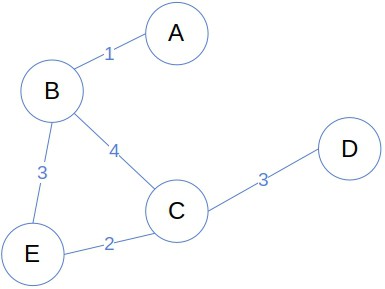
A weighted graph is a graph that costs money when moving two vertices.

Complete graph

A complete graph is a graph in which all vertices are connected by edges.

Exploration of the graph.

Depth First Search (DFS)

Depth-first search DFS is a method of traversing the graph by going as deep as possible and returning to the previous vertex if there is nowhere else to go. Implement it simply using recursion or using a stack.

Breadth First Search (BFS)

Breadth-first search BFS is a method in which a starting vertex is visited, all vertices adjacent to the starting vertex are visited, and then all vertices adjacent to the starting vertex are visited first. This is usually implemented by using QUEUE to enqueue everything that can go from the current location.

Reference

1. https://coding-factory.tistory.com/610
2. https://mathinsight.org/definition/undirected_graph
3. https://mathinsight.org/definition/directed_graph
4. https://www.baeldung.com/cs/weighted-vs-unweighted-graphs
5. https://mathworld.wolfram.com/CompleteGraph.html