동적 프로그래밍 Dynamic Programming💃 (with fibonacci)

두선아 Dusuna·2023년 4월 8일

동적 프로그래밍 Dynamic Programming💃 (with fibonacci)

📌 캐싱을 사용하는 최적화 기법

최적화 문제를 해결

중복된 연산을 피하기 위해 사용

작은 하위 문제들의 해결책을 조합 ⇒ 전체 문제를 해결

📌 주로 사용되는 예제

피보나치 수열

Longest Common Substring (최장 공통 부분 문자열)

0/1 Knapsack Problem (0/1 배낭 문제)

그래프의 최단 경로

📌 추가 문제
1. House Robber
2. Best Time to Buy and Sell Stock
3. Climbing Stairs

CodeSandbox : 코드 샌드박스 예제 페이지

동적(다이나믹) 프로그래밍이란?

분할 정복 Divide & Conquer과 메모이제이션 Memozation의 결합입니다.

🤔 다이나믹 프로그래밍을 고려하기

문제를 하위 문제로 나눌 수 있는가? - recursion
재귀로 해결하는 문제인가? - tree
하위 문제가 반복적인가? - yes
Memoize할 수 있는가? - let's go!

👉 문제를 작은 하위 문제로 쪼갤 수 있고, 반복적인 재귀 해결책들의 해결책 또는 결과를 캐싱하여, 성능을 개선할 수 있을 때 사용합니다.

1. Overlapping Subproblems 중복되는 하위 문제

큰 문제를 하위 문제로 쪼갭니다.
하위 문제들은 서로 중복될 수 있습니다.
중복된 하위 문제들을 한 번만 해결하고 저장하여, 중복된 계산을 피합니다.

2. Optimal Substructure 최적 부분 구조

부분 문제의 최적 해결책을 조합하여 최적의 해결책을 구합니다.

3. Top-down + Memoization 메모이제이션 📌

하위 문제의 해결책을 저장하고 재사용합니다.

4. Bottom-up Approach

부분 문제의 최적 해결책을 구한 후, 이를 이용하여 전체 문제의 최적 해결책을 구합니다.

Memoization

캐싱 Caching

문제에 대한 해결책을 기억합니다.
algorithms\dynamic-programming\memoizationDP.js

let cache = {
  // property에 접근 : O of One Time
  1: 81,
};

function memoizedAddTo80(n) {
  if (n in cache) {
    return cache[n];
  } else {
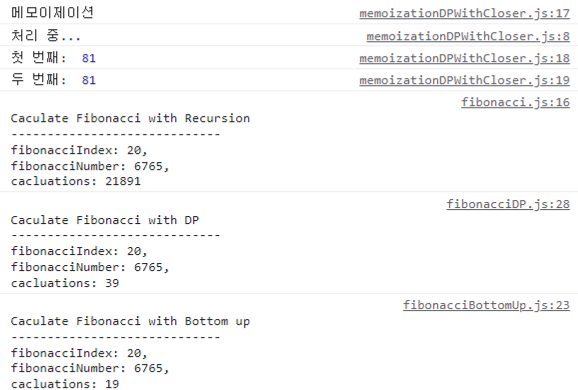
    console.log("처리 중...");
    cache[n] = n + 80;
    return cache[n];
  }
}

console.log("첫 번째: ", memoizedAddTo80(1)); // 81, 연산 후 캐싱
console.log("두 번째: ", memoizedAddTo80(1)); // 81, O of One

클로저 Closer

global 변수가 아닌 클로저를 사용합니다.
algorithms\dynamic-programming\memoizationDPWithCloser.js

function memoizedAddTo80WithCloser(n) {
  let cache = {};

  return function (n) {
    if (n in cache) {
      return cache[n];
    } else {
      console.log("처리 중...");
      cache[n] = n + 80;
      return cache[n];
    }
  };
}

const memoized = memoizedAddTo80WithCloser(); // cache 변수와 내부 함수 반환

console.log("첫 번째: ", memoized(1)); // 81, 연산 후 캐싱
console.log("두 번째: ", memoized(5)); // 85, 연산 후 캐싱
console.log("세 번째: ", memoized(5)); // 85, O of One

클로저를 이용하여 cache 객체를 선언하고, 해당 함수 내부에서만 접근할 수 있도록 변수 환경에 저장합니다. 이후 함수를 호출할 때마다 해당 변수 환경에서 cache 객체를 활용하여 이미 계산된 값을 반환하게 됩니다. 이렇게 함으로써, 전역 변수를 사용하지 않고도 값을 캐싱하고 재사용함으로써 성능을 향상시킬 수 있습니다.
- 실행 컨텍스트 내부의 변수 환경에 객체를 저장합니다.
  ✏️ 실행 컨텍스트
  
  코드 실행에 필요한 변수, 함수 선언, 매개변수 등의 정보를 담고 있는 스택(Stack) 자료구조 형태(LIFO)
  - 구분: Variable Environment, Lexical Environment, This Binding
  - 생성: 코드를 실행할 때
  - 제거: 함수 실행이 종료될 때
클로저 함수를 다음과 같이 사용할 수 없는 이유를 묻는다면...
```
console.log("첫 번째: ", memoizedAddTo80WithCloser()(1));
console.log("두 번째: ", memoizedAddTo80WithCloser()(1));
```
✏️ memoizedAddTo80WithCloser()함수는 내부에서 캐싱을 위한 cache변수와 내부 함수를 반환합니다.

매번 memoizedAddTo80WithCloser() 함수가 호출될 때마다 cache 객체가 초기화됩니다. 그렇기 때문에 cache 객체에 저장된 값은 재사용되지 않고 매번 새로 계산됩니다.

즉,memoizedAddTo80WithCloser()(1)과 memoizedAddTo80WithCloser()(1) 의 결과는 서로 다를 수 있습니다.

변수를 함수가 최초 호출될 때 cache 객체가 생성되고, 이후 호출에서 계산 결과를 재사용하는 캐싱을 사용할 수 있습니다.

Fibonacci 피보나치 배열

Recursion 재귀를 사용하는 피보나치 배열

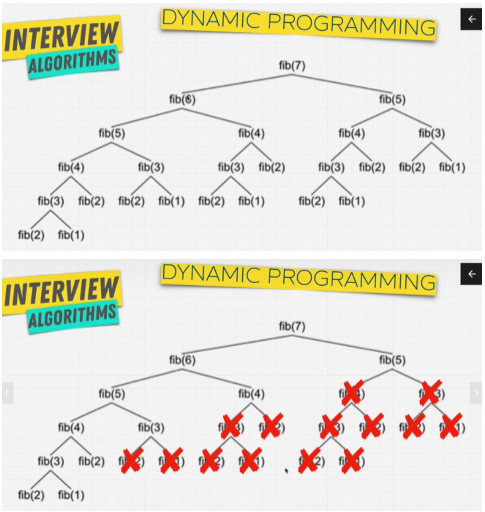
O(2^N) : O of Two the the power of N
9번째 index를 구하기 위해, 109번의 계산이 필요함
20번째 index를 구하기 위해, 21891번의 계산이 필요함

let cacluations = 0;
function fibonacci(n) {
  cacluations++;

  if (n < 2) {
    return n;
  }
  return fibonacci(n - 1) + fibonacci(n - 2);
}

const fibonacciIndex = 9;
const fibonacciNumber = fibonacci(fibonacciIndex);

console.log(`
  fibonacciIndex: ${fibonacciIndex}, 
  fibonacciNumber: ${fibonacciNumber}, 
  cacluations: ${cacluations}
`);

피보나치와 Dynamic Programming : 반복되는 하위 문제의 해결책

반복되는 하위 문제
- 하위 문제의 계산을 캐싱하여 최적화할 수 있습니다.
  - fib(1), fib(2), fib(3)… 와 같은 문제가 반복됩니다.

동적 프로그래밍의 메모이제이션 적용하기

📎 Top-down 방식은 일반적으로 재귀적인 방식으로 문제를 해결하는 방식에서 시작합니다. 하지만 이때, 중복되는 계산을 피하기 위해 memoization(메모이제이션)을 적용합니다.

즉, 문제를 재귀적으로 해결하면서 이미 계산한 결과를 메모해 놓고, 같은 계산이 다시 나타나면 메모한 결과를 리턴하는 방식입니다. 이를 통해 중복 계산을 피할 수 있어서 계산 속도를 대폭 개선할 수 있습니다.

Top down + memoization 방식 / 하향식 암기법
algorithms\dynamic-programming\fibonacciDP.js

let cacluations = 0;

function fibonacciFn() {
  let cache = {}; // 해시 테이블에 피보나치 계산값을 캐싱합니다.

  return function fib(n) {
    cacluations++;
    if (n in cache) {
      return cache[n];
    } else {
      if (n < 2) {
        return n;
      } else {
        cache[n] = fib(n - 1) + fib(n - 2);
        return cache[n];
      }
    }
  };
}

const fibDP = fibonacciFn(); // 변수에 함수를 할당

const fibonacciIndex = 20;
const fibonacciNumber = fibDP(fibonacciIndex);

// if fibonacciIndex: 9, cacluations: 109
// O of Two to the Power of N
console.log(`
Caculate Fibonacci with DP
-----------------------------
fibonacciIndex: ${fibonacciIndex}, 
fibonacciNumber: ${fibonacciNumber}, 
cacluations: ${cacluations}
`);

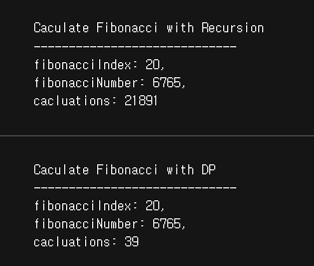
피보나치 배열 : O(2^n) ⇒ O(n)

다이나믹 프로그래밍을 통해 모든 연산를 한 번씩 실행하는, O(n)의 속도를 가집니다.
- 공간 복잡성 Space Complexity이 올라감
- 시간 복잡성 Time Complexity이 낮아짐
피보나치는 시간 복잡성 절약이 아주 큰 경우입니다.

다른 방법 : Bottom up

📎 Bottom-up 방식은 동적 프로그래밍은 주어진 문제의 해결을 위해, 작은 부분 문제들의 해결을 먼저 구하고, 이들의 해결 결과를 이용하여 보다 큰 문제의 해결을 차례대로 구해나가는 방법입니다.

Bottom-up 동적 프로그래밍은 주어진 문제의 해결을 위해, 작은 부분 문제들의 해결을 먼저 구하고, 이들의 해결 결과를 이용하여 보다 큰 문제의 해결을 차례대로 구해나가는 방법입니다.
- Bottom-up 방식은 일반적으로 재귀 호출에 비해 반복문을 사용하여 구현하는 것이 효율적입니다.
- 코드가 더 복잡해질 수 있으나, 모든 부분 문제를 해결하고 최종 결과를 얻어내는 과정이 명확하고 직관적이기 때문에, 상황에 따라 유용하게 사용될 수 있습니다.
피보나치 예시
```
// fibonacciBottomUp 함수 정의, n을 인자로 받음
function fibonacciBottomUp(n) {
  // 초기값 설정
  let answer = [0, 1];

  for (let i = 2; i <= n; i++) {
    answer.push(answer[i - 2] + answer[i - 1]);
    // i-2번째와 i-1번째 항을 더한 값을 answer 배열에 추가
  }

  // 구한 값들 중 n번째 값 반환
  return answer.pop();
}
```
📎 함수 내부에서 answer 배열을 선언하고, 초기값으로 [0, 1]을 할당합니다. 이후 for 문을 통해 배열에 추가할 값을 계산하며, 마지막에 answer.pop()을 통해 n번째 항을 반환합니다.

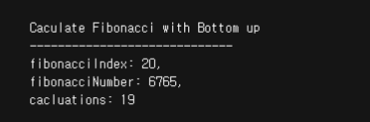
Bottom-up 방식에서는 계산해야 하는 값을 작은 단위부터 계산해나가기 때문에 재귀 호출에 비해 더 빠른 속도로 수열을 구할 수 있습니다.

결론 🌱

재귀를 사용하여 반복적인 연산을 하는 함수에 동적 프로그래밍 기법을 사용할 수 있다.

closer를 의식적으로 활용해보자.

동적 프로그래밍에 대한 예제를 풀어보자.

피보나치 수열

Longest Common Substring (최장 공통 부분 문자열)

0/1 Knapsack Problem (0/1 배낭 문제)

그래프의 최단 경로

House Robber

Best Time to Buy and Sell Stock

Climbing Stairs

콘솔 내용처럼 calcuations 횟수를 개선할 수 있다.

두선아 Dusuna

안녕하세요.

이전 포스트

CSS: Skeleton UI 적용기

다음 포스트

동적 프로그래밍 Dynamic Programming💃 (with fibonacci)

동적 프로그래밍 Dynamic Programming💃 (with fibonacci)

동적(다이나믹) 프로그래밍이란?

🤔 다이나믹 프로그래밍을 고려하기

1. Overlapping Subproblems 중복되는 하위 문제

2. Optimal Substructure 최적 부분 구조

3. Top-down + Memoization 메모이제이션 📌

4. Bottom-up Approach

Memoization

캐싱 Caching

클로저 Closer

Fibonacci 피보나치 배열

Recursion 재귀를 사용하는 피보나치 배열

피보나치와 Dynamic Programming : 반복되는 하위 문제의 해결책

동적 프로그래밍의 메모이제이션 적용하기

피보나치 배열 : O(2^n) ⇒ O(n)

다른 방법 : Bottom up

결론 🌱

CSS: Skeleton UI 적용기

⚠ 깃허브 commit의 작성자 변경하기(위험, feat. git-filter-repo)

0개의 댓글

동적 프로그래밍 Dynamic Programming💃 (with fibonacci)

동적 프로그래밍 Dynamic Programming💃 (with fibonacci)

동적(다이나믹) 프로그래밍이란?

🤔 다이나믹 프로그래밍을 고려하기

1. Overlapping Subproblems 중복되는 하위 문제

2. Optimal Substructure 최적 부분 구조

3. Top-down + Memoization 메모이제이션 📌

4. Bottom-up Approach

Memoization

캐싱 Caching

클로저 Closer

Fibonacci 피보나치 배열

Recursion 재귀를 사용하는 피보나치 배열

피보나치와 Dynamic Programming : 반복되는 하위 문제의 해결책

동적 프로그래밍의 메모이제이션 적용하기

피보나치 배열 : O(**2^n**) ⇒ O(n)

다른 방법 : Bottom up

결론 🌱

CSS: Skeleton UI 적용기

⚠ 깃허브 commit의 작성자 변경하기(위험, feat. git-filter-repo)

0개의 댓글

피보나치 배열 : O(2^n) ⇒ O(n)