한국방송통신대 알고리즘 강의 2강 정리노트입니다.

---

알고리즘 분석

정확성 분석

유효한 입력에 대해 유한 시간 내에 정확한 결과의 생성 여부이다.

• 수학적 기법을 사용한 이론적인 증명 과정

효율성 분석

알고리즘 수행에 필요한 컴퓨터 자원의 양을 측정/평가한다.

공간 복잡도 Space complexity

메모리의 양 = 정적 공간 + 동적 공간

시간 복잡도 Time complexity

수행 시간 = 알고리즘의 실행에서부터 완료까지 걸리는 시간

실제 수행시간을 측정하는 것은 실행 환경에 종속적이므로 일반적이지 않다. 알고리즘 수행시간은 각 문장이 수행되는 횟수를 계산한 다음 이를 더한 합으로 구할 수 있다.

수행 시간에 영향을 미치는 요인으로는 1) 입력 크기, 2) 입력 데이터의 상태가 있다. 따라서 단순히 단위 연산이 수행되는 개수의 합으로 표현하는 것은 부적절하다.

1. 입력 크기 n이 커질 수록 수행시간이 증가하므로, 입력 크기 n의 함수 f(n)으로 표현한다.
2. 알고리즘의 우열을 따지기 위해서는 최악의 수행시간으로서 표현해야 한다.

점근 성능 Asymptotic Analysis

입력 크기 n이 무한히 커짐에 따라 결정되는 성능

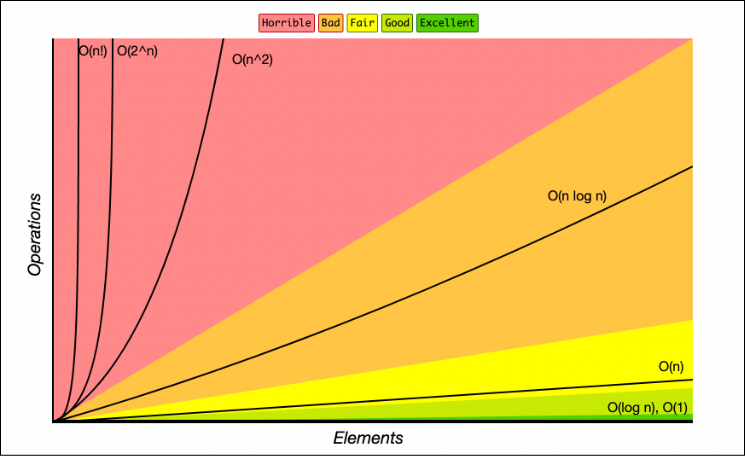
• 입력 크기가 충분히 커짐에 따라 함숫값에 가장 큰 영향을 미치는 차수를 찾는다.
• 수행시간의 다항식 함수에서 최고차항만을 계수 없이 취하여 표현한다.
  • ex) 2n -> n

점근 성능은 정확한 값이 아닌 어림값으로, 수행시간의 증가 추세를 파악하는 것이 쉽고, 알고리즘 간의 우열을 따질 때 유용하다.

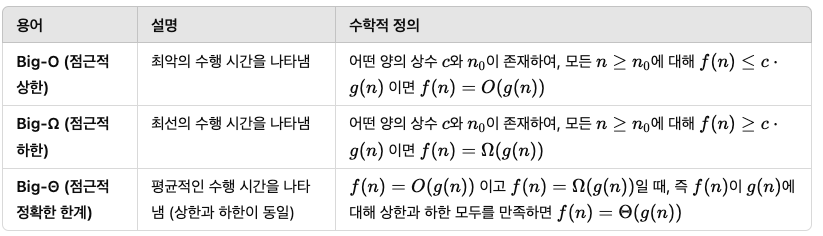
• Big-O(빅오): 최악의 경우에 대한 상한선을 나타내며, 주어진 입력에 대해 알고리즘이 얼마나 빨리 최악의 상태에서 실행될지 나타낸다.
• Big-Ω(빅오메가): 최선의 경우에 대한 하한선을 나타내며, 알고리즘이 입력에 대해 최상의 성능을 보일 때 걸리는 시간이다.
• Big-Θ(빅세타): 알고리즘의 성능이 상한과 하한 모두를 만족할 때 사용되며, 알고리즘의 수행 시간이 정확히 어떻게 변화하는지 나타낸다.

실용성을 위하여 알고리즘의 모든 문장이 아닌, 루프의 반복 횟수만을 조사하여 최고 차수를 시간 복잡도로 취합니다.

순환 알고리즘의 성능

• 기본 점화식과 폐쇄형
  

점화식 형태	설명	예시 상황	시간 복잡도 추정
(T(n) = T(n-1) + O(1))	이전 단계에서 상수 작업 추가	반복문 1번 돌면서 상수 작업 추가하는 경우	O(n)
(T(n) = T(n-1) + n)	이전 단계에서 n 크기 작업 추가	1단계씩 진행하며, 단계마다 점점 더 큰 작업 추가하는 경우	O(n²)
(T(n) = T(n/2) + O(1))	절반으로 줄이면서 상수 작업 추가	이진 탐색처럼, 매번 문제 크기 절반으로 줄이면서 상수 작업	O(log n)
(T(n) = T(n/2) + n)	절반으로 줄이면서 n 크기 작업 추가	병합 정렬처럼, 나누고 병합하는데 병합이 선형 시간	O(n log n)
(T(n) = 2T(n/2) + O(1))	절반 두 개로 나누고, 상수 작업 추가	분할 정복 기본 구조 (단순한 분할-정복 문제)	O(n)
(T(n) = 2T(n/2) + n)	절반 두 개로 나누고, 각 단계에서 n 크기 작업 추가	병합 정렬, 퀵 정렬 (분할 후 병합/정렬)	O(n log n)

예시

알고리즘	점화식 형태	시간 복잡도
선형 탐색	(T(n) = T(n-1) + O(1))	O(n)
퀵 정렬(최악)	(T(n) = T(n-1) + O(1))	O(n²)
이진 탐색	(T(n) = T(n/2) + O(1))	O(log n)
병합 정렬, 퀵 정렬(최선)	(T(n) = 2T(n/2) + n)	O(n log n)