한국방송통신대 알고리즘 강의 5강 정리노트입니다.
📌 힙 정렬 Heap Sort
- 최선, 최악, 평균 수행시간이 O(n log n)
- 안정적이지 않은 정렬
- 제자리 정렬 알고리즘
힙 Heap
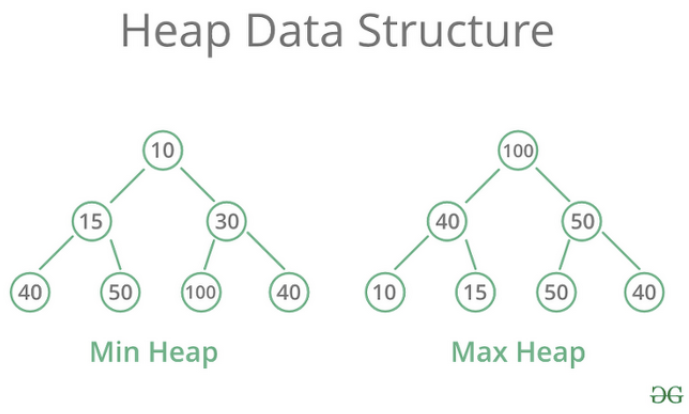
임의의 값 삽입과 최댓값 혹은 최소값 삭제가 쉬운 완전 이진 트리, 우선순위 큐 자료 구조입니다.
https://www.geeksforgeeks.org/heap-data-structure/
- 완전 이진트리 Complete binary tree
- 모든 레벨이 채워져있고, 마지막 레벨은 왼쪽부터 채워짐
- 즉, 0~마지막 노드의 값이 전부 존재함
- 최대 힙 max heap: 각 노드의 값이 자신의 자식 노드보다 크거나 같음
- 최소 힙 min heap: 각 노드의 값이 자신의 자식 노드보다 작거나 같음
형태
힙은 1차원 배열로 표현합니다.
heap = [10, 20, 30, 40, 50, 60, 70, 80] # 최소 힙
index = 2
left_child = 2 * index + 1 # 30의 왼쪽 자식 노드는 5번째 인덱스인 60
right_child = 2 * index + 2 # 30의 왼쪽 자식 노드는 6번째 인덱스인 70
parent = heap[(index - 1) // 2] # 30의 부모는 0번째 인덱스인 10배열 인덱스 계산
- 왼쪽 자식 노드: 2i + 1
- 오른쪽 자식 노드: 2i + 2
- 부모 노드: (i-1) / 2
삽입과 삭제
heap은 우선순위 큐 자료구조이며, 삽입/삭제의 시간복잡도는 O(log n)입니다.
- 임의의 값 삽입: 마지막 노드에 넣은 후, Heapfy Up (Bubble Up) 과정을 거침
- 삭제: 루트 노드를 제거한 후 마지막 요소를 루트로 이동하고, Heapfy Down (Bubble Down) 과정을 거친다.
힙 정렬 과정
1차원 배열을 힙으로 만들기
힙 정렬을 위해 힙 구조를 만듭니다.
가장 큰 값을 루트에서 O(1)로 바로 접근하기 위해 최대 힙을 사용합니다.
배열 배치 & 힙 구조 복원
def heap_sort(arr):
n = len(arr)
# 일차원 배열을 힙으로 구축
for i in range(n // 2 - 1, -1, -1):
heapify(arr, n, i)
# 최대 힙에서 가장 큰 값을 추출하여 배열에 배치
for i in range(n - 1, 0, -1):
arr[0], arr[i] = arr[i], arr[0] # 루트를 배열 끝으로 보내기
heapify(arr, i, 0) # 힙 구조 복원
return arr
# 자식 노드와 비교하여 힙 구조를 복원
def heapify(arr, n, i):
largest = i
left = 2 * i + 1
right = 2 * i + 2
# 왼쪽 자식이 범위 내이고, 왼쪽 자식이 부모보다 크면 큰 자식으로 설정
if left < n and arr[left] > arr[largest]:
largest = left
# 오른쪽 자식이 범위 내이고, 오른쪽 자식이 부모보다 크면 큰 자식으로 설정
if right < n and arr[right] > arr[largest]:
largest = right
# 부모가 자식보다 크면 교환 후 재귀 호출
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i]
heapify(arr, n, largest)📌 비교 기반 알고리즘 vs 비교 기반이 아닌 알고리즘
Comparison-Based Algorithms vs Non-comparative Algorithms
비교 기반 알고리즘은 두 원소를 비교하여 그들의 상대적인 순서를 정하는 방식으로 동작합니다. 대표적인 알고리즘으로는 버블 정렬, 삽입 정렬, 병합 정렬, 퀵 정렬, 힙 정렬 등이 있습니다.
비교 기반의 정렬 알고리즘의 성능 하한은 O(n log n)입니다. 최소 O(n log n) 번의 비교가 필요한 이론적 한계점이 있습니다.
계수/버킷/기수 알고리즘은 특정 조건 하에서 빠른 정렬이 가능합니다. 원소에 대한 비교 없이 이미 얻어진 데이터 분포 정보를 활용하여 정렬합니다.
선형 시간 O(n), O(n + k) 시간 복잡도의 연산이 가능합니다.
📌 계수 정렬 Counting Sort
원소의 등장 횟수를 세는 방식입니다.
- 시간 복잡도는 O(n + k), 즉 O(n)
- 입력값의 범위 n이 데이터의 개수 k보다 작거나 비례할 때 선형 시간을 보장
- 안정적인 정렬 알고리즘
- 제자리 정렬이 아님, 공간 복잡도는 O(k)
계수 정렬은 원소들의 범위가 정해져 있는 경우에 사용하는 정렬로, 각 원소가 몇 번 등장하는지 카운트합니다.
그 이후, 같거나 작은 요소를 확인해, 각 입력값의 출현 횟수의 누적값을 계산합니다. 누적값은 각 요소가 나타날 마지막 위치를 나타냅니다.
누적값을 계산한 후 원본 배열을 뒤에서부터 순회하며 정렬을 실행할 때, 정렬한 요소는 누적값을 -1하여 다음에 나타날 위치를 업데이트 합니다.
뒤에서부터 순회하는 이유는 안정적인 정렬을 위해서입니다.
def counting_sort(arr):
max_val = max(arr)
min_val = min(arr)
count = [0] * (max_val - min_val + 1)
result = [0] * len(arr)
# 카운트 배열 채우기
for num in arr:
count[num - min_val] += 1
# 누적합 구하기
for i in range(1, len(count)):
count[i] += count[i - 1]
# 원본 배열을 뒤에서부터 순회하여 정렬
for i in range(len(arr)-1, -1, -1):
num = arr[i] # 현재 값
index = count[num - min_val] - 1 # 현재 값이 들어갈 위치
result[index] = num # 현재 값을 결과 배열에 넣기
count[num - min_val] -= 1 # 위치 업데이트
return result📌 기수 정렬 Radix Sort
원소를 자리수에 따라 정렬합니다.
- 시간 복잡도는 O(dn), d(digit)을 상수로 간주하면 O(n)
- 정수 혹은 길이가 고정된 문자열일 경우 사용
- 안정적인 정렬 알고리즘
- 각 자릿수별로 안정적인 정렬 알고리즘을 수행
- 제자리 정렬이 아님, 공간 복잡도는 O(n + k)
주어진 데이터의 값을 자릿수로 나누고, 각 자릿수에 대해 안정적인 정렬 알고리즘을 적용합니다.
자릿수가 적고 원소가 많을 때 빠르게 동작할 수 있습니다.
LSD, Least Significant Digit
LSD 기수 정렬은 자릿수의 작은 곳(일의 자리)부터, 오른쪽에서부터 왼쪽으로 진행합니다.
자릿수를 기준으로 정렬합니다. (1의 자리 → 10의 자리 → 100의 자리 순)
고정된 자릿수의 짧은 숫자 그리고 작은 범위에서 효율적이며, 배열을 반복해서 정렬하기 때문에 메모리 사용이 일정합니다.
def counting_sort_number(arr, exp):
n = len(arr)
output = [0] * n
count = [0] * 10 # 0~9까지의 숫자 카운팅
# 해당 자릿수에서 숫자 개수 세기
for num in arr:
index = (num // exp) % 10
count[index] += 1
# 누적 합 계산하여 정렬된 위치 결정
for i in range(1, 10):
count[i] += count[i - 1]
# 정렬된 결과 생성
for i in range(n - 1, -1, -1):
index = (arr[i] // exp) % 10
output[count[index] - 1] = arr[i]
count[index] -= 1
# 원본 배열 업데이트
for i in range(n):
arr[i] = output[i]
def radix_sort(arr):
max_num = max(arr)
exp = 1 # 자릿수 (1의 자리, 10의 자리, 100의 자리 ...)
while max_num // exp > 0:
counting_sort_number(arr, exp)
exp *= 10 # 다음 자리로 이동
arr = [170, 45, 75, 90, 802, 24, 2, 66]
radix_sort(arr)MSD, Most Significant Digit
MSD 기수 정렬은 자릿수의 큰 곳(가장 왼쪽)부터, 왼쪽에서 오른쪽으로 진행합니다.
문자열을 정렬할 경우 맨 앞 글자부터 정렬하기 위해 사용하거나, 숫자가 고정된 자릿수가 아닐 때, 긴 숫자일 때 가장 큰 자릿수부터 정렬하는 것이 효율적일 수 있습니다.
def msd_radix_sort(arr, pos=None):
if not arr or len(arr) == 1:
return arr
if pos is None:
max_val = max(arr)
pos = len(str(max_val)) - 1 # 가장 높은 자릿수 찾기
buckets = [[] for _ in range(10)]
for num in arr:
digit = (num // (10 ** pos)) % 10 # 현재 자릿수의 숫자 추출
buckets[digit].append(num)
sorted_arr = []
for bucket in buckets:
if bucket:
sorted_arr.extend(msd_radix_sort(bucket, pos - 1 if pos > 0 else None))
return sorted_arr
arr = [170, 45, 75, 90, 802, 24, 2, 66]
print(msd_radix_sort(arr)) # 출력: [2, 24, 45, 66, 75, 90, 170, 802]📌 버킷 정렬 Bucket Sort
- 평균 시간 복잡도: O(n + k), 여기서 n은 정렬할 요소의 수, k는 버킷의 수
- 최악의 경우 시간 복잡도: O(n²), 모든 요소가 하나의 버킷에 들어가는 경우
- 안정적인 정렬 알고리즘
- 제자리 정렬이 아님, 공간 복잡도는 O(n + k)
버킷 정렬은 데이터 분포에 민감합니다. 입력 데이터가 특정 버킷에 집중되면 성능이 크게 저하됩니다.
커밋의 개수가 n/k일 때, 각 버킷에 평균적으로 k개의 요소가 들어갑니다.
k가 상수라면 n개의 버킷에 대해 총 O(n × k²), 즉 O(n) 시간이 소요됩니다.
정렬 단계
- 버킷 만들기 (주어진 데이터의 값의 범위를 균등하게 나누기)
- 각 버킷에 각 데이터 삽입
- 각 버킷을 삽입 정렬과 같은 안정적인 정렬 수행
- 버킷 순서대로 데이터를 나열
def bucket_sort(arr, bucket_size=5):
if len(arr) == 0:
return arr
min_val = min(arr)
max_val = max(arr)
bucket_count = (max_val - min_val) // bucket_size + 1
buckets = [[] for _ in range(bucket_count)]
for num in arr:
bucket_index = (num - min_val) // bucket_size
buckets[bucket_index].append(num)
sorted_arr = []
for bucket in buckets:
sorted_arr.extend(sorted(bucket))
return sorted_arr개념 정리
힙 정렬
힙 구조의 장점(임의의 값 삽입과 최대값 삭제가 쉬움)을 활용한 정렬 방식
두 단계의 처리 과정, 두 가지의 초기 힙 구축 방법
시간 복잡도: O(n log n)
특징: 불안정적, 제자리계수 정렬
데이터 분포 기반 → 입력값의 범위가 데이터의 개수보다 작거나 비례하는 경우
시간 복잡도: O(n)
특징: 안정적, 제자리 정렬이 아님기수 정렬
데이터 분포 기반 → 입력 데이터의 자릿수가 상수인 경우
시간 복잡도: O(n)
특징: 안정적, 제자리 정렬이 아님