소수를 구하는 알고리즘

N-1까지의 정수로 나누기

def find_prime_list_under_number(number):
	prime_list = []

	for n in range(2, number+1):
  		for i in range(2, n):
      		if n%i == 0 :
        	break
   		else: prime_list.append(n)

   	return prime_list
   
print(find_prime_list_under_number(20))

소수의 특성을 이용하기

입력값이 소수인지 판별하는 코드

import math

def find_prime(n):
    for i in range(2, math.floor(math.sqrt(n))+1):
        if(n%i==0):
            return False
    return True

print(find_prime(n))

입력값 범위의 소수 개수 구하는 코드

import math


def find_prime(n):
    for i in range(2, math.floor(math.sqrt(n)) + 1):
        if (n % i == 0):
            return False
    return True


def find_prime_total(n):
    count = 0
    for i in range(2, n + 1):
        if find_prime(i):
            count += 1
    return count


n = 100
print(find_prime(n))
print(find_prime_total(n))

에라토스테네스의 체

이해하기

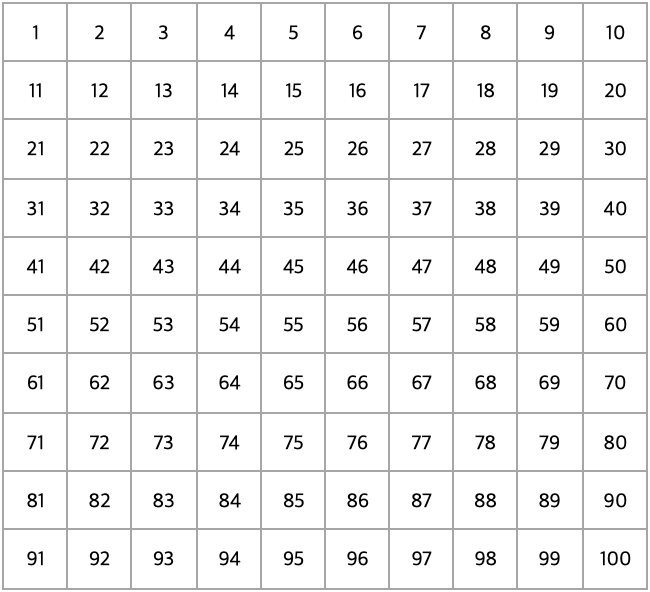
1 제거 후, 2를 제외한 2의 배수 제거.

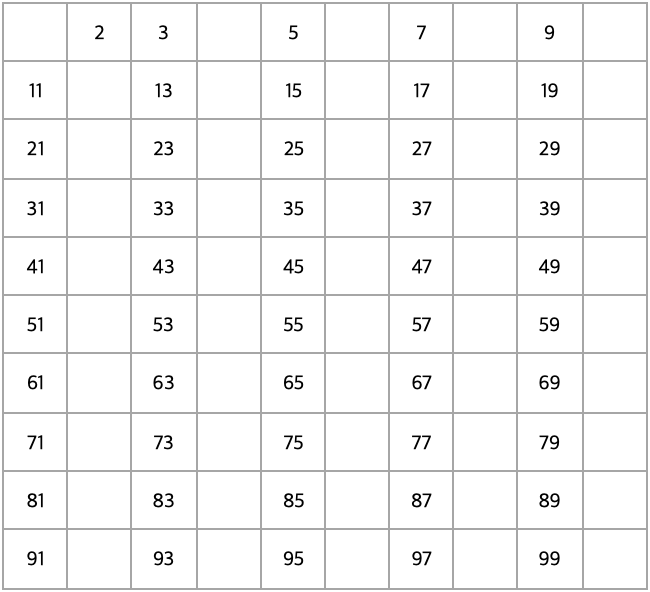
3을 제외한 3의 배수 제거.

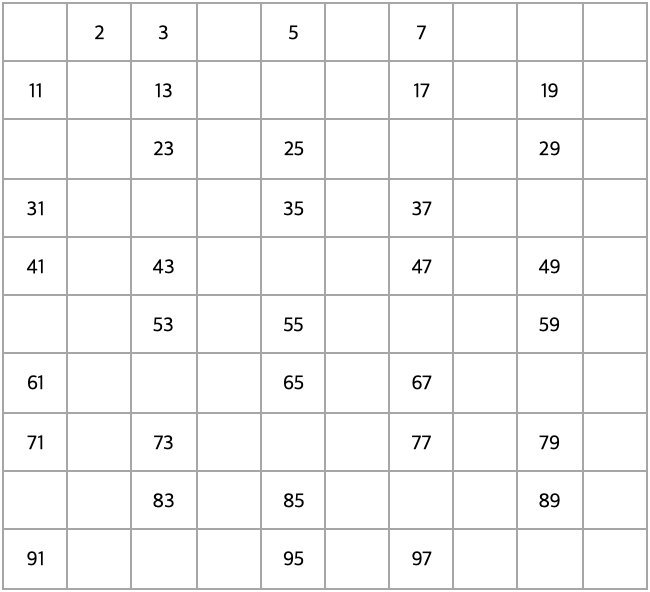
4의 배수는 이미 모두 지워졌다. 5을 제외한 5의 배수 제거

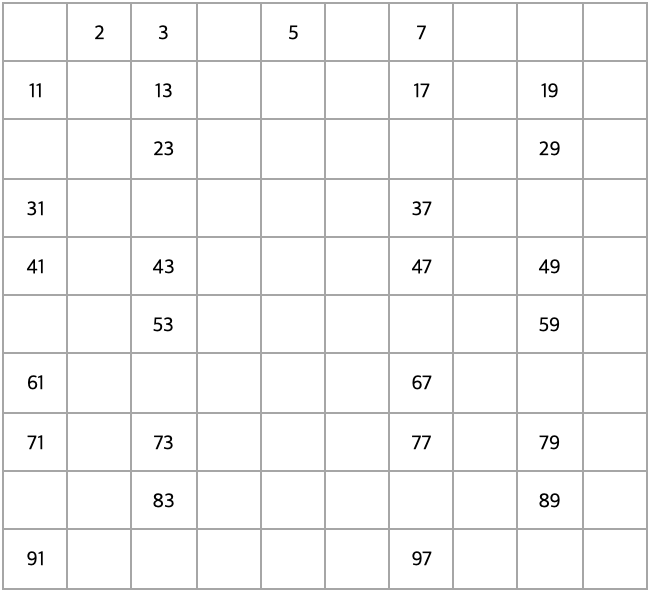
7을 제외한 7의 배수 제거

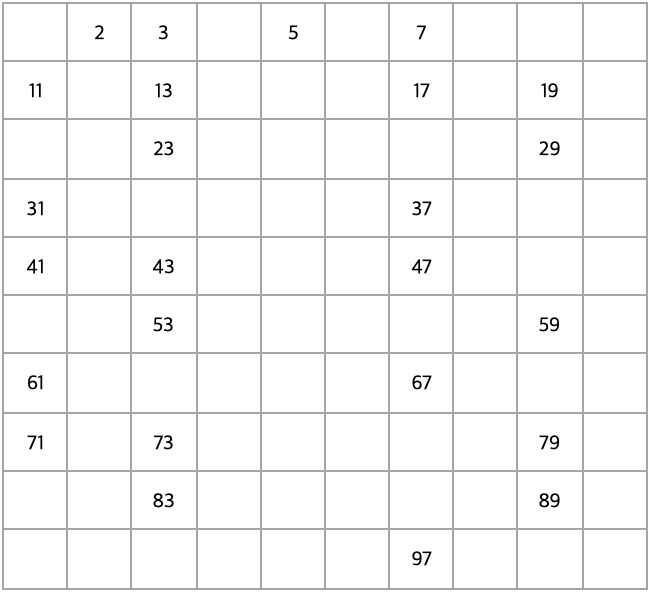
11 > $\sqrt100$ $(=10)$ 이므로 고려 대상이 아니다.
왜냐면, 예를 들어 8의 경우 $2\times4 = 4\times2$ 와 같은 식으로 대칭을 이루기 때문에 특정한 숫자의 제곱근까지만 약수의 여부를 검증하면 된다.

입력값 이하의 모든 소수를 출력하는 코드

def find_prime_list_under_number(n):
    # sieve[0], sieve[1]은 False로 제외시키고 sieve[2]부터 (n-1)까지 True로 설정한다.
    # n-1을 하는 이유는 sieve[1]을 뺴야 하기 때문이다.

    sieve = [False,False]+[True]*(n-1)
    primes = []

    for i in range(2,n+1):
        if sieve[i] :
            primes.append(i)
        # i의 배수를 제외 시키기, i의 첫번째 배수 i*2 부터 n까지, i만큼 증가시키면서
        for j in range (i*2,n+1,i) :
            sieve[j] = False

    print(primes)
    print(len(primes))