백준 Q1753 - 최단경로

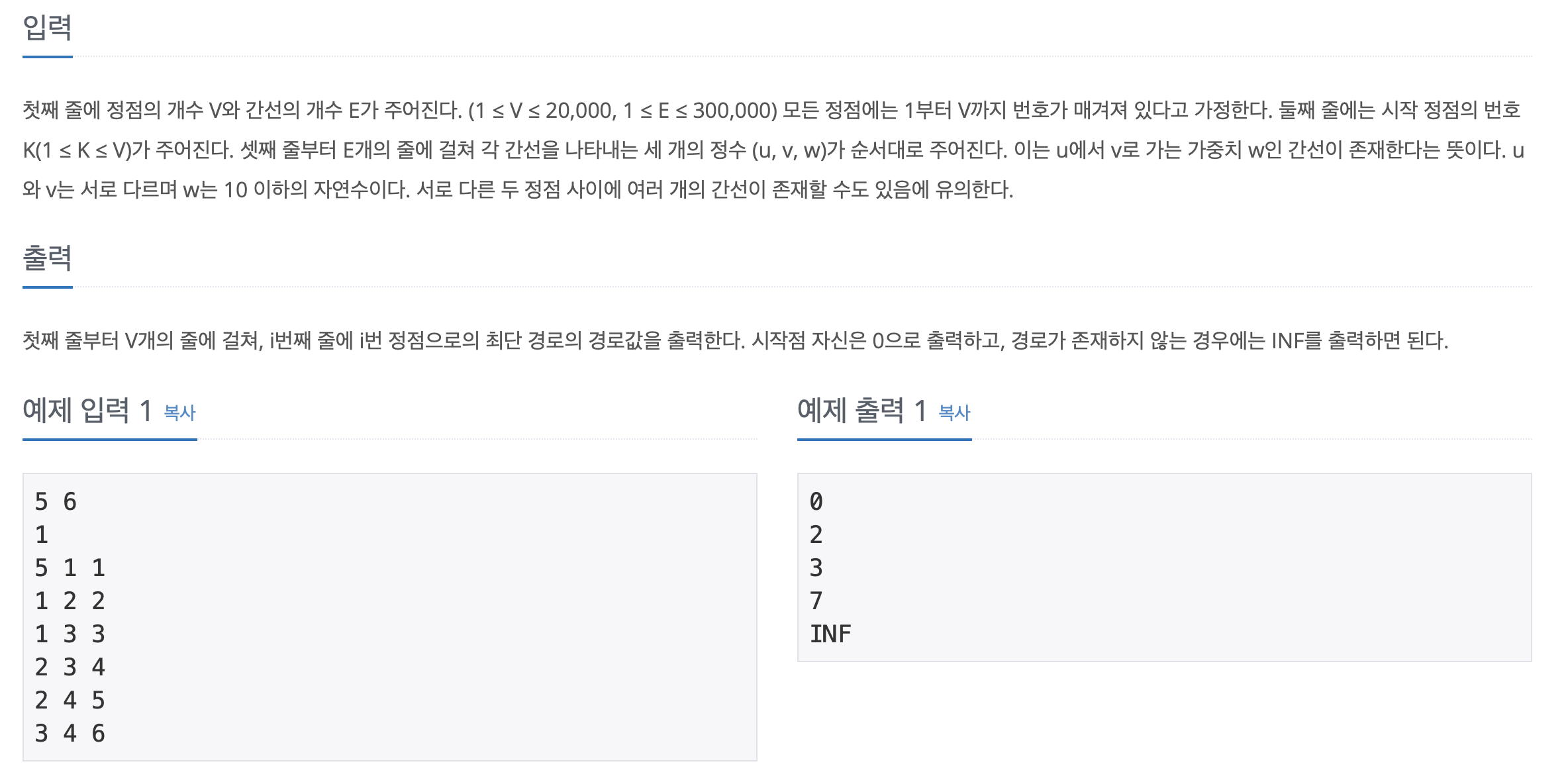
문제 및 입출력

---

풀이

그래프의 모든 노드를 순회하며 탐색하는것이 아닌 최단경로를 구하는 문제이다.
최적의 경로를 구하기 위해 다익스트라 알고리즘을 떠올렸다.

static int V, E, start;
static List<Node>[] graph;
static boolean[] visited;
static int[] distance;

변수 설명

• V, E, start: 정점의 개수, 간선의 개수, 시작 노드
• graph: 자료형이 Node인 리스트를 담을 배열
• visited: 방문여부를 체크하는 배열
• distance: 최적의 경로를 구하기 위한 거리를 나타내는 배열

입력 1,2,3 에 대해 "노드1->노드2 의 가중치3" 을 2차원 배열로 표현하려 했으나
방향성이 존재하고, 이후 큐를 활용할때 어려움이 있을것 같아 리스트형 배열로 풀이하였다.

distance = new int[V + 1];
	for (int i = 1; i < V + 1; i++) {
		distance[i] = Integer.MAX_VALUE;
	}
distance[start] = 0;

distance 배열을 정점의 개수+1 만큼 초기화하고, 각 노드의 값을 무한대를 표현하기 위해 가장 큰 값으로 채워넣는다
초기 시작하는 노드인 start=1에서 node1 -> node1 의 가중치는 0이다

for (int i = 0; i < E; i++) {
	st = new StringTokenizer(br.readLine());
	int u = Integer.parseInt(st.nextToken());
	int v = Integer.parseInt(st.nextToken());
	int w = Integer.parseInt(st.nextToken());
	graph[u].add(new Node(v, w));
}

PriorityQueue<Node> queue = new PriorityQueue<>();
queue.add(new Node(start, 0));

방향성이 존재하므로 단방향으로만 그래프를 만들어준다
또한 각 노드->노드마다 가중치가 존재하기 때문에 필드가 node,value 인 Node 클래스를 정의하여 사용하자

static class Node implements Comparable<Node> {
	int node;
	int value;

	public Node(int node, int value) {
		this.node = node;
		this.value = value;
	}

	@Override
	public int compareTo(Node o) {
		return Integer.compare(this.value, o.value); 
	}
}

1. 왜 우선순위 큐를 사용하는가?
2. 우선순위 큐를 사용할때 항상 Comparable or Comparator를 implements 하여 오버라이딩 해야하는가?

우선순위큐는 일반적으로 오름차순이다
-> 1. 최단경로를 찾기위한 다익스트라 알고리즘을 사용하기 위해서는 사용자가 정의한 값으로 오름차순 or 내림차순을 하고, 중요도 순서대로 큐에서 뽑아서 사용해야 하므로 우선순위 큐를 사용한다.

-> 2. 아니다. 임의의 클래스로 구성된 우선순위 큐 or 기본 타입이지만 우선순위를 바꾸고 싶은 경우에만 오버라이딩을 하여 메서드를 재정의하면 되고, 이 문제는 전자의 경우에 해당한다.

while (!queue.isEmpty()) {
	Node current = queue.poll();
	int node = current.node;

	if (visited[node]) continue;
	visited[node] = true;

	for (Node tmp : graph[node]) {
		int nextNode = tmp.node;
		int value = tmp.value;
		if (!visited[nextNode] && distance[nextNode] > distance[node] + value) {
			distance[nextNode] = distance[node] + value;
			queue.add(new Node(nextNode, distance[nextNode]));
		}
    }
}

---

최종 코드

public class Main {
    static int V, E, start;
    static List<Node>[] graph;
    static boolean[] visited;
    static int[] distance;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        V = Integer.parseInt(st.nextToken());
        E = Integer.parseInt(st.nextToken());
        start = Integer.parseInt(br.readLine());

        graph = new List[V + 1];
        for (int i = 1; i <= V; i++) {
            graph[i] = new ArrayList<>();
        }

        visited = new boolean[V + 1];
        distance = new int[V + 1];
        for (int i = 1; i < V + 1; i++) {
            distance[i] = Integer.MAX_VALUE;
        }
        distance[start] = 0;

        for (int i = 0; i < E; i++) {
            st = new StringTokenizer(br.readLine());
            int u = Integer.parseInt(st.nextToken());
            int v = Integer.parseInt(st.nextToken());
            int w = Integer.parseInt(st.nextToken());
            graph[u].add(new Node(v, w));
        }

        PriorityQueue<Node> queue = new PriorityQueue<>();
        queue.add(new Node(start, 0));

        while (!queue.isEmpty()) {
            Node current = queue.poll();
            int node = current.node;

            if (visited[node]) continue;
            visited[node] = true;

            for (Node tmp : graph[node]) {
                int nextNode = tmp.node;
                int value = tmp.value;
                if (!visited[nextNode] && distance[nextNode] > distance[node] + value) {
                    distance[nextNode] = distance[node] + value;
                    queue.add(new Node(nextNode, distance[nextNode]));
                }
            }
        }

        StringBuilder sb = new StringBuilder();

        for (int i = 1; i <= V; i++) {
            if (visited[i]) sb.append(distance[i]).append("\n");
            else sb.append("INF").append("\n");
        }
        System.out.println(sb);
    }

    static class Node implements Comparable<Node> {
        int node;
        int value;

        public Node(int node, int value) {
            this.node = node;
            this.value = value;
        }

        @Override
        public int compareTo(Node o) {
            return Integer.compare(this.value, o.value); // 가중치 기준 오름차순 정렬
        }
    }
}

---

풀이 후기

distance[nextNode] = distance[node] + value;
queue.add(new Node(nextNode, distance[nextNode]));

여기서 새로운 노드를 생성하며 큐에 넣을때, 연결되어 있는 다음 노드와 해당 노드까지의 거리를 파라미터로 생성한다.

근데 이미 윗 줄에서 distance[nextNode] 를 통해 새로운 최적의 거리 가중치값을 할당 했는데 왜 생성자로 해당값을 초기화해야 하는지, 그냥 current 값을 넣으면 되지 않은가 고민을 했다

다익스트라 알고리즘은 가중치가 낮은 노드를 큐에서 먼저 탐색을 하기 위해 우선순위 큐를 사용하는 근본적인 이유에 있었다.
새로 업데이트한 distance[nextNode]를 생성자에 넣지 않고 current의 value를 넣어버리면 큐에서 우선순위가 꼬이기 때문이다.