본 글에서 사용한 코드는 모두 Google Colab에서 실행함

📌 선형회귀분석의 프로세스

---

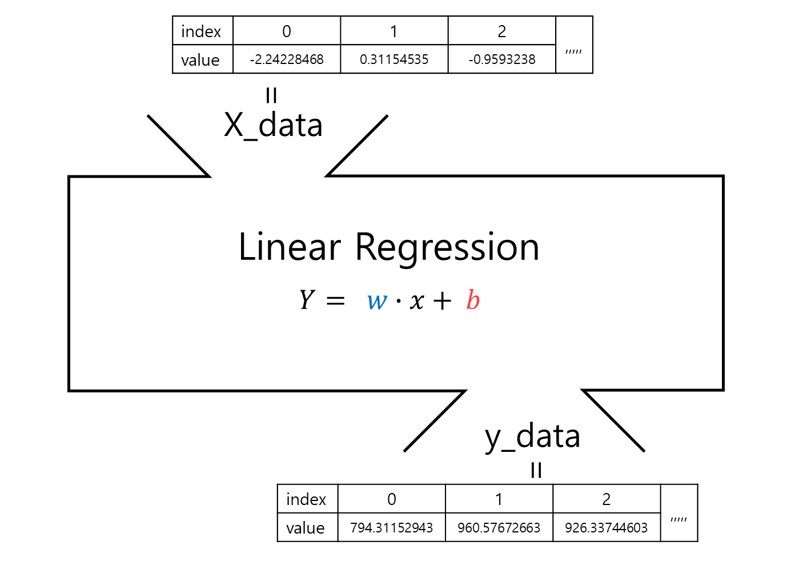
💻 가상의 데이터로 예측하기

📌 코드 실행 명령어 및 파라미터
make_regression(n_samples, n_features, bias, noise)

• Scikit-Learn의 datasets 서브패키지는 회귀분석용 가상 데이터를 생성하는 명령어인 make_regression()을 제공한다.
• make_regression()으로 만들어진 데이터는 종속변수 y의 값이 독립변수 x 벡터의 선형 조합인 선형관계를 가진다.

📌 주요 parameter :

• n_samples : 표본 데이터의 갯수, (정수, 기본값 = 100)
• n_features : 독립변수의 수(차원), (정수, 기본값 = 100)
• n_target : 종속변수의 수, (정수, 기본값 = 1)
• bias : y절편 (실수, 기본값은 0.0)
• noise : 분포 (기본값은 0.0)
• random_state : 시드 --> 랜덤 샘플 추출시 같은 시드에서는 항상 같은 결과를 도출함

(1) 회귀분석용 가상 데이터를 생성

✍ 입력

#회귀분석용 가상 데이터 생성
from sklearn.datasets import make_regression

# 1000개의 데이터(sample), 1개의 특성(feature)을 가진 랜덤한 데이터 셋을 생성해보자.
data = make_regression(n_samples = 1000, n_features = 1, bias = 1000, noise = 50, random_state = 333) 
data

#data[0] --> X_data, data[1] --> y_data로 할당시키기
X_data = data[0]
y_data = data[1]
X_data, y_data

💻 출력

1014.63062833,  937.276929  , 1028.85458691,  999.53195253,
921.52617314, 1108.42245836,  973.74776871, 1104.50833387,
815.4892863 , 1008.77223671,  959.34100589, 1102.00840217,
861.91592663, 1013.76055433,  902.17295613,  968.90531028,
1052.40785324,  934.45015553, 1148.73290621,  988.99041207,
…

생성한 1000개의 데이터를 x,y에 할당하고 출력

✍ 입력

# 랜덤 데이터 셋을 DataFrame으로 변환시켜보자.
import pandas as pd

random_df = pd.DataFrame()
random_df['X_data'] = X_data.flatten()
random_df['y_data'] = y_data

# 데이터프레임의 첫 케이스 5개를 출력시켜보자.
random_df.head()

💻 출력

📈 위에 생성한 가상 데이터 셋을 그래프 나타내기

scatter() : matplotlib의 pyplot 패키지에서는 산점도를 그릴 수 있는 명령어

✍ 입력

from matplotlib import pyplot as plt
%matplotlib inline 
# notebook을 실행한 브라우저에서 바로 그래프를 볼 수 있게 하는 기능

plt.scatter(data[0], data[1]) 
plt.show() #그래프 표시

💻 출력

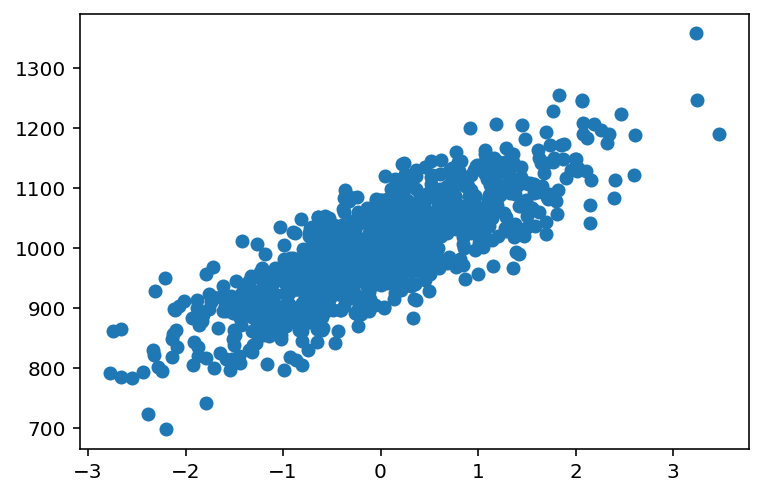
임의로 생성한 가상 데이터의 분포를 나타낸 산점도이다. 선형적으로 분포되어있는 데이터인 걸 알 수 있다.

(2) 선형 모델 생성

train_test_split(data, data2, test_size, train_size, shuffle, random_state)

• Scikit-Learn의 model_selection패키지는 데이터를 학습용(train)과 검증용(test)으로 분리시켜주는 명령어 train_test_split()을 제공한다.

📌 주요 parameter :

• data: 독립변수(X) 데이터
• data2: 종속변수(y) 데이터 --> data 인수에 종속변수(y)가 포함되어 있다면 생략 가능
• test_size: 검증용 데이터의 개수/비율 --> 1 이하의 실수일 경우 비율을 나타냄 (기본값 = 0.25)
• train_size : 학습용 데이터의 개수/비율 --> 1 이하의 실수일 경우 비율을 나타냄 (기본값 = 0.25), test_size와 train_size 중 하나만 사용 가능
• shuffle: 데이터 섞기 (기본값은 True)
• random_state: 난수 생성
• fit_intercept: y 절편(bias) 계산 여부, (기본 값 = True)
• normalize: 데이터 셋 정규화, (기본 값 = False)

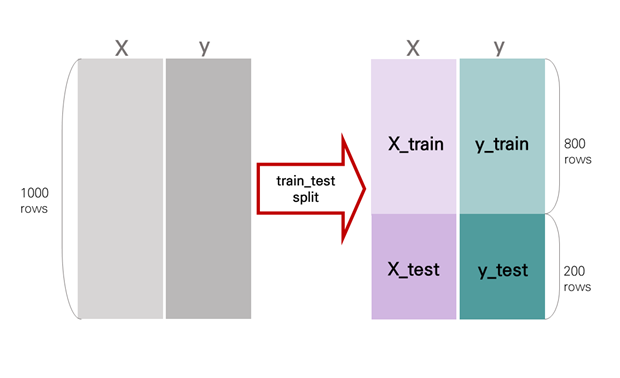
train_test_split 이후 데이터는 위 그림과 같이 분할된다.

✍ 입력

# 학습용과 검증용으로 데이터 분리하는 명령어 실행
from sklearn.model_selection import train_test_split

# 생성한 가상의 데이터를 학습용 데이터(train data)와 검증용 데이터(test data)로 나누어 보자.
X_train, X_test, y_train, y_test = train_test_split(X_data, y_data, test_size = 0.2, shuffle = True)

from sklearn.linear_model import LinearRegression

# LinearRegression을 hypothesis라는 변수에 대입해 보자. 그대로 사용해도 무방하지만 쓰기에 너무 기니까 변수에 대입해서 사용해보자.
hypothesis = LinearRegression()

(3) 모델 학습

✍ 입력

# fit() 명령어를 통해 학습 데이터를 학습시킨 모델을 model_linear라는 변수에 대입해보자.
model_linear = hypothesis.fit(X_train, y_train)

(4) 모델의 weight(가중치,계수)와 bias 출력

속성
.coef_ : 각 입력 특성에 하나씩 대응되는 weight의 numpy 배열
.intercept_ : 모델의 bias (y절편)값을 나타냄

✍ 입력

# coef_ 명령어를 통해 model_linear의 계수(=weight)을 살펴보자.
model_linear.coef_

# 앞서 생성한 데이터에는 입력 특성(feature)이 하나이므로 이에 대응하는 계수 하나만 출력된다.

💻 출력

array([74.26301693])

✍ 입력

# intercept_ 명령어를 통해 model_linear의 y 절편(=bias)를 살펴보자.
# intercept_ 속성은 항상 실수 값 한 개이다.
model_linear.intercept_

💻 출력

998.9515308498641

📈 훈련용 데이터의 산점도와 선형회귀직선 시각화

regplot(x, y, data) : seaborn 라이브러리의 repplot()은 X, Y 축 값의 산점도와 선형 회귀 직선을 함께 시각화함

주요 parameters:

• x: X data/ dataframe의 features 칼럼
• y: y data/ dataframe의 target 칼럼
• data: 칼럼이 속한 데이터프레임

✍ 입력

import seaborn as sns
sns.regplot(X_train, y_train)

💻 출력

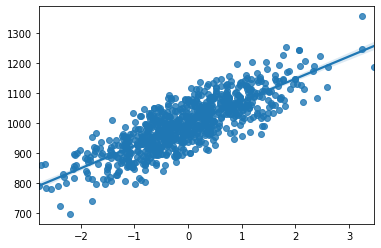
📈 테스트용 데이터의 산점도와 선형회귀직선 시각화

✍ 입력

sns.regplot(X_test, y_test)

💻 출력

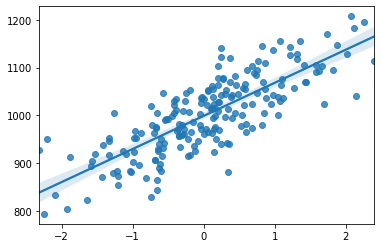
훈련용 데이터의 시각화에 비해 데이터 양이 적고 회귀선에서 더 퍼져있는 걸 확인할 수 있다.

(5) 모델 검증

score() 명령어 : 모델 성능 검증 & R2 score 값 반환
(R2 score = 결정계수; 회귀모델의 설명력을 나타내며 최고값이 1임)

✍ 입력

# 앞서 학습시킨 model_linear의 성능을 살펴보자.
print("학습 데이터 점수 : {:.2f}".format(model_linear.score(X_train, y_train)))
print("검증 데이터 점수 : {:.2f}".format(model_linear.score(X_test, y_test)))

💻 출력

학습 데이터 점수 : 0.67
검증 데이터 점수 : 0.63

보통 검증 데이터 점수보다 학습 데이터 점수가 높은게 일반적이다.
학습과 검증은 4%의 성능 차이를 보인다.

✍ 입력

# predcit() 명령어를 사용하여 y값을 예측한다.
y_predict = model_linear.predict(X_test)

from sklearn.metrics import mean_squared_error

# 실제 값(y_test)과 예측값(y_predict)을 이용하여 mean squared error을 측정해보자.
mse = mean_squared_error(y_test, y_predict)

# root mean squared error를 측정해보자.
import numpy as np
rmse = np.sqrt(mse)

# 사이킷런에서 RMSE를 계산하는 명령어를 제공하고 있지 않기 때문에 MSE에 루트를 씌워 직접 계산하여야 한다.
# sqrt는 루트를 씌워주는 명령어이다.

# mean squared error와 이에 루트를 씌운 root mean squared error을 각각 출력해보자.
print('MSE : {:.3f}, RMSE : {:.3f}'.format(mse, rmse))

💻 출력

MSE : 2822.958, RMSE : 53.132

MSE와 RMSE 값을 통해 회귀분석의 결정계수를 구해보자.

✍ 입력

from sklearn.metrics import r2_score

# 실제 값(y_test)과 예측값(y_predict)을 이용하여 R2 score을 측정하고 출력해보자.
print('R2 : {:.2f}'.format(r2_score(y_test, y_predict)))

#model_linear.score(X_test, y_test)와 동일한 값이 나온 것을 확인할 수 있다.

💻 출력

R2 : 0.61

결정계수 $R^2$ 0.61로, 독립변수 x가 종속변수 y의 61% 정도를 설명한다고 할 수 있다.