실수란 무엇인가?
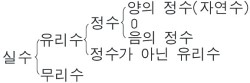
실수 : 소수 부분을 포함하는 수
소수 : 0과 1사이이 수 ex)0.1, 0.3 ...
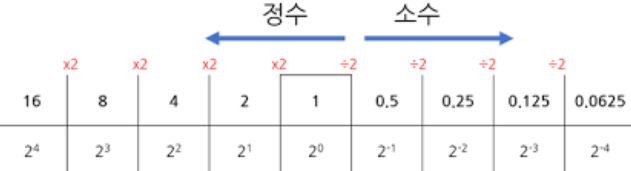
밑이 2인 경우, 실수를 표기하기 위한 방법이 필요하고 정수와 마찬가지로
실수를 표현하는 방법이 다르다.
고정소수점 표현법
- 2진 소수점의 위치를 임의로 정하는 방법
따라서 실수를 표현하는 가장 간단한 방식은 소수부의 자릿수를 미리 정하여,
고정된 자릿수의 소수를 표현하는 것입니다.
Ex)

문제점
-
고정 소수점 표현법은 쓸모 있는 범위의 실숫 값을 나타내기 위해 많은 비트를 필요로 하기 때문에 범용컴퓨터에서 사용하지 않는 방법이다.
범용 컴퓨터 : 사무처리에서 과학기술 계산, 문서처리, 도형처리까지 폭넓게 대응할 수 있는 다용도 컴퓨터 비트를 많이 필요로 한다 : 메로리 비용이 많이 든다. -
DSP(디지털 처리 신호장치) 등 일부 컴퓨터에서는 사용된다.
부동소수점 표현법
- 넓은 범위의 값을 2진수로 표현하기를 위해 '과학적 표기법(scientific notation)을 2진수에 적용한다.
- 플랑크 상수부터 아보가드로 수에 이르는 범위의 값을 2진수로 표현한다는 문제를 해결하기 위해 적용한 과학적 표기법 이다.
- 소수점의 위치가 정해져있지 않다.
*과학적 표기법에선 10진 소수점 왼쪽이 한 자리뿐인 소수에 10을 몇 번 거듭제곱한
값을 곱하는 방식으로 소수를 표현한다.Ex)

가수 : 소수점 왼쪽
- 과학적 표기법처럼 밑이 10이 아닌 2를 밑으로 표기 하고 가수 부분은 2진 소수, 지수 부분은 2의 거듭제곱 횟수를 표현한 표현법을 부동 소수점이라고 합니다.

문제점
- 중복되는 표현 방법이 있어서 비효율적이다.
- 비트 패턴이 가능한 모든 수를 표현하지 못한다.
ex)0.5 + 0.5 = 1.0 (O) / 6.5 비트 패턴이 없기 때문에 0.5+6.0 더할 수 없음.
IEEE 부동소수점 수 표준
- 부동소수점 수 시스템은 컴퓨터에서 계산을 수행할 때 실수를 표현하는 표준 방법이다.
- 부동소수점 비트 패턴보다 더 많은 비트를 사용하고, 가수와 지수에 대해 각각의 부호 비트를 가지고 있지만 지수에 대한 부호 비트는 지수의 비트 패턴에 감춰져 있다.
- 낭비되는 비트 조합을 최소화하고 반올림을 쉽게 하기 위한 여러가지 트릭을 사용한다.
여러가지 트릭
1) 정규화 트릭
: 정규화는 가수를 조정해서 맨 앞에 0이 없게 만드는 것. 가수를 조정함으로 지수 또한 조정을 해야 된다.
2) 디지털 이퀍먼트 사에서 고안한, 가수의 맨 왼쪽 비트가 1이라는 사실을 알고 있으므로 이를 생략하는 것. 이로 인해 가수에 1 비트를 더 사용할 수 있게 된다.
IEEE754(IEEE 754는 IEEE에서 개발한 컴퓨터에서 부동소수점을 표현하는 가장 널리 쓰이는 표준이다)
-
기본 정밀도 부동 소수점 수 : 32비트 사용, 7비트 정밀도로 대략 10의 38상 범위 표현
-
2배 정밀도 부동 소수점 수 : 64비트를 사용하기에 더 많은 범위를 표현 할 수 있다.
정밀도 : 정밀도는 실수를 얼마나 정확하게 저장할 수 있는지에 대한 정도를 나타내는 것
->2배 정밀도 수는 기본 정밀도 수보다 29비트가 크기에 정밀도가 훨씬 더 크지만 그만큼 비용을 많이 지불하고 얻은 것.
IEEE754의 편리한 점
- 0으로 나눴을때 양의 무한대, 음의 무한대를 표현하는 비트 패턴등 여러가지 특별한 비트 패턴을 제공한다.
- ‘수가 아님’이라는 뜻의 NaN을 표현하는 특별한 값이 있다.
-> 이로 인해 부동 소수점 수로 계산을 하던 도중 Nan 값이 생기면 뭔가 잘못된 산술 연산을 수행했다는 것을 알 수 있다.
