(전공복습) 진법 변환 구현

디지털논리회로 강의를 수강하면서, 진법변환에 대한 내용을 배워서 공부삼아 구현해보았다.

10진수 -> n진수

1. 들어온 수 n을 소수와 정수로 나눈다. ex)45.75 => quo = 7, fra=0.75
2. 정수의 경우 n진수로 계속 나누며 나머지를 저장한다.
3. 소수의 경우 n진수로 계속 곱하며 소숫점을 저장한다.

또한 중요한것은 저장된 값은 역으로 읽어줘야한다(스택을 사용하면 될듯)

예를들어, 45.75를 7진수로 바꾸려면 정수는 45, 소수는 0.75이며
45/7 = 6...3 이며 6/7 = 0...6이므로 스택1에는 6,3이 저장된다.
소수는 0.75이므로 0.757 = 5.25(5와 0.25), 0.257 = 1.75(1과 0.75)... 계속적인 반복이다.

따라서 스택1은 정수만 계산한 값인 63, 스택2는 소수만 계산한 값인 5,1,5,1 반복.

결과적으로 문자열에 붙여주며 출력하면 끝!

import java.util.*;

public class Main {
    static Stack<Integer> stack1 = new Stack<>();     //정수부분
    static Stack<Integer> stack2 = new Stack<>();     //소수부분
    static String res = "";

    static void divide(String n, int radix){     //소수와 정수 분리. 변환할 n과 몇진수로 변환할 지.
        double quo,fraction = 0;
        if(n.contains(".")) {       //소숫점이 있는 숫자일 경우.
            quo = Double.parseDouble(n.substring(0, n.indexOf(".")));     //소숫점 앞의 정수부분.
            fraction = Double.parseDouble(n) - quo;      //소수부분.
        }
        else{       //소숫점이 없을 때.
            quo = Double.parseDouble(n);
            fraction = 0;
        }
        quo_recursive((int)quo,radix);
        fra_recursive(fraction,0,radix);
    }

    static void quo_recursive(int r, int radix){
        if(r == 0)
            return;       //소수부분만 리턴.
        stack1.push(r%radix);
        quo_recursive(r/radix,radix);
    }

    static void fra_recursive(double f,int cnt, int radix){
        if(cnt >= 10 || f == 0){      //제한을 10번정도로 두고 무한대로 계산할 수 있기때문에 종료시킴..
            return;
        }
        else {
            fra_recursive(f * radix - (int) (f * radix), cnt+1, radix);
            stack2.push((int) (f * radix));
        }
    }

     public static void main (String[]args){
         Scanner scanner = new Scanner(System.in);
         int radix = scanner.nextInt();        //decimal -> what radix?
         String number = scanner.next();    //input transfer number(input decimal number)

         divide(number,radix);

        while(!stack1.isEmpty()){
            res += String.valueOf(stack1.pop());
        }
        if (number.contains("."))
            res += ".";

         while(!stack2.isEmpty()){
             res += String.valueOf(stack2.pop());
         }

         System.out.print(res);
    }
}

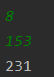
1. 8진수로 153을 변환
   
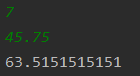
2. 7진수로 45.75를 변환
   
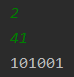
3. 2진수로 41을 변환
   

재귀를 응용해서 풀 수 있지만, 캐스팅이 많이 일어나기 때문에 효율적이지는 않다.(소숫점때문에 문자열을 써야하는 것이 조금 아쉽당..)

n진수 -> 10진수

이번엔 역으로 n진수를 10진수로 만드는 것을 구현해 보았다.

예시1) n=2, input=110.11을 변환한다면 1x2^2 + 1x2^1 + 0x2^0 + 1x2^-1 + 1x2^-2 = 6.75가 된다.

예시2) n=8, input = 231은 2x8^2 + 3x8^1 + 1x8^0 = 153이 된다.

import java.util.*;

public class Main {
    static int idx1,idx2;
    static double num1, num2;
    static String f,q;
     public static void main (String[]args){
         Scanner scanner = new Scanner(System.in);
         int radix = scanner.nextInt();
         String input = scanner.next();

         if(input.contains(".")) {
             q = input.substring(0, input.indexOf("."));
             f = input.substring(input.indexOf(".") + 1);
         }
         else{
             q = input;
             f = "0";
         }
         int pos1 = q.length()-1;
         int pos2 = -1;

         while (pos1 >= 0){     //정수부분
             num1 += (Character.getNumericValue(q.charAt(idx1++)) * Math.pow(radix,pos1));
             pos1--;
         }

         int a = 0 - f.length();    //pos2의 경우 -1,-2..r^n-1로 간다.
         while (pos2 >= a){     //소수부분
             num2 += (Character.getNumericValue(f.charAt(idx2++)) * Math.pow(radix,pos2));
             pos2--;
         }
         System.out.print(num1 + num2);


    }
}

이것을 구현하기 위해서 각 문자열마다의 연산이 필요하므로 String으로 처리 하였고, Character.getNumericValue(q.charAt(idx1++))을 통해서 한글자씩 계산한 뒤 넘기는 방식으로 구현하였다.