TFMaster
1.2장. Perceptron 퍼셉트론
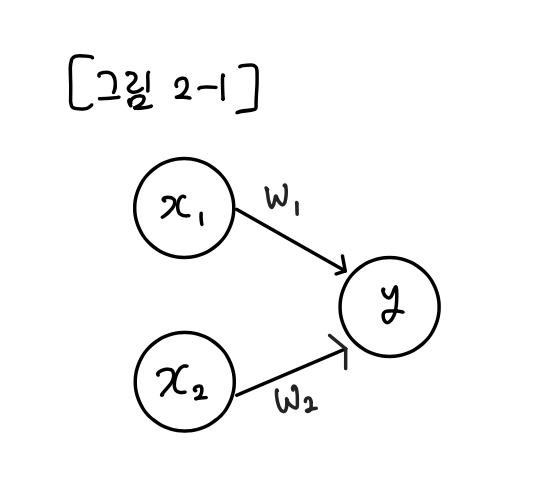
퍼셉트론은 프랑크 로젠블라트(Frank Rosenblatt)가 1957년에 고안한 알고리즘이며, 지금까지도 신경망(딥러닝)의 기원이 되는 알고리즘이다. 앞으로의 아이디어들을 배우기 위해 퍼셉트론의 구조를 배우는 것이 중요하다. 퍼셉트론은 입력으로 다수의 신호를 받으며
2.3장. 신경망

앞선 포스팅에선 2장. 퍼셉트론에 대해 공부하였다. 앞장에서 배운 내용에 관련해서 좋은 소식/나쁜 소식이 있다. 좋은 소식 : 퍼셉트론으로 복잡한 함수도 표현할 수 있다. 나쁜 소식 : 가중치를 설정하는 작업(원하는 결과를 출력하도록 적절히 정하는 작업)은 여전히 사람
3.4장-1. 신경망 학습
여기서 학습이란 훈련 데이터로부터 가중치 매개변수의 최적값을 자동으로 획득하는 것을 뜻한다. 이번 포스팅에선 신경망이 학습할 수 있도록 해주는 지표인 손실함수(Loss Function)을 소개한다. 이 Loss function의 결과값을 가장 작게 만드는 가중치 매개변
4.4장-2. 신경망 학습
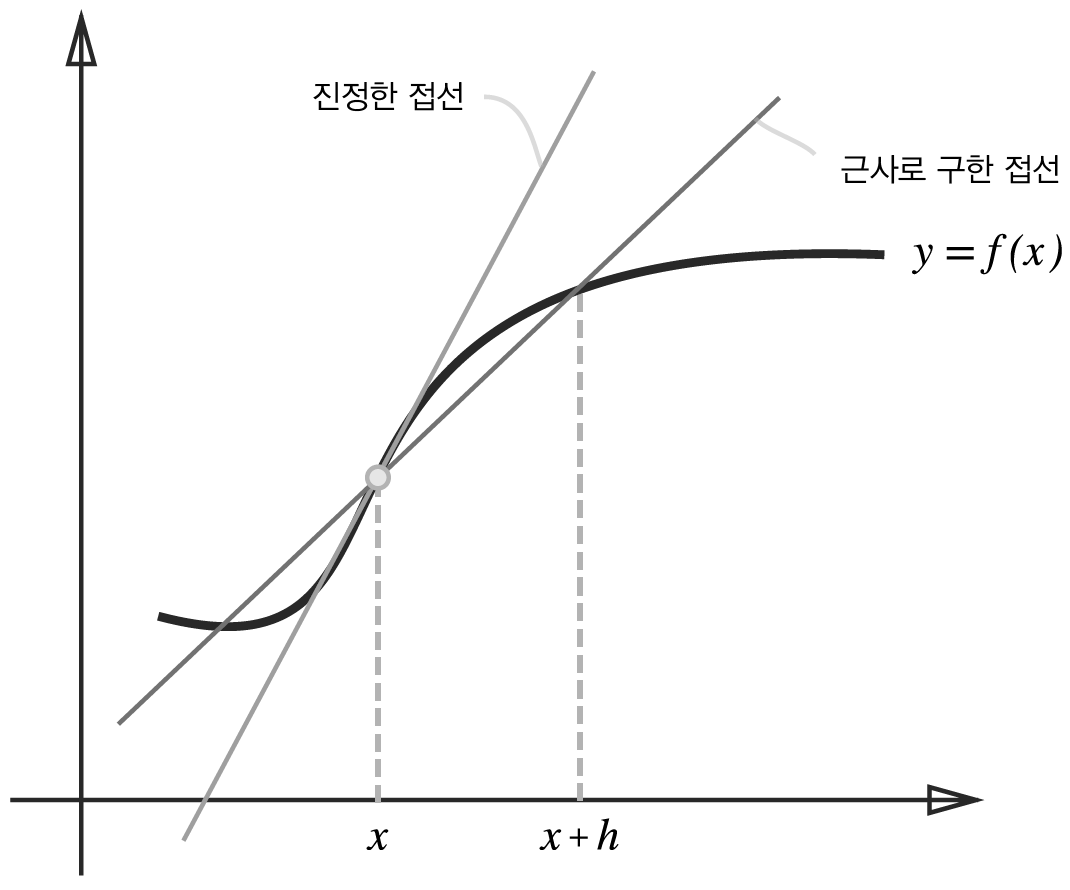
수치 미분 (numerical differentiation) 경사법에서는 기울기(경사) 값을 기준으로 나아갈 방향을 정한다. 미분 우리가 마라톤 선수이고 처음부터 10분에 2km씩 달렸다 치자. 이때의 속도는 간단히 2 / 10 = 0.2 km/m이라 계산할 수 있따
5.5장. 오차역전파법 backpropagation - 1

앞 포스팅에서의 수치미분은 단순하고 구현하기도 쉽지만 시간이 오래 걸린다는 것이 단점이다. 가중치 매개변수의 기울기를 효율적으로 계산하는 오차역전파법(backpropagation)을 이야기해보자. 이해하는 방법은 2가지가 있다. 수식을 통한 것 계산 그래프(compu
6.5장. 오차역전파법 backpropagation - 2

구체적인 구현에 들어가기 전에 신경망 학습의 전체 그림을 복습해 보자. 다음은 신경망 학습의 순서이다.전제신경망에는 적응 가능한 가중치와 편향이 있고, 이 가중치와 편향을 훈련 데이터에 적응하도록 조정하는 과정을 '학습'이라 한다. 신경망 학습은 다음과 같이 4단계로
7.6장. 학습 관련 기술들 - 1

오늘은 학습에 관련된 기술들에 대해서 얘기해볼 것이다. 매개변수 갱신 신경망 학습의 목적은 손실 함수의 값을 가능한 한 낮추는 매개변수를 찾는 것이다. 이는 곧 최적값을 찾는 문제이며, 이러한 문제를 푸는 것은 최적화(optimization)이라 한다. 지금까지는
8.6장. 학습 관련 기술들 - 2
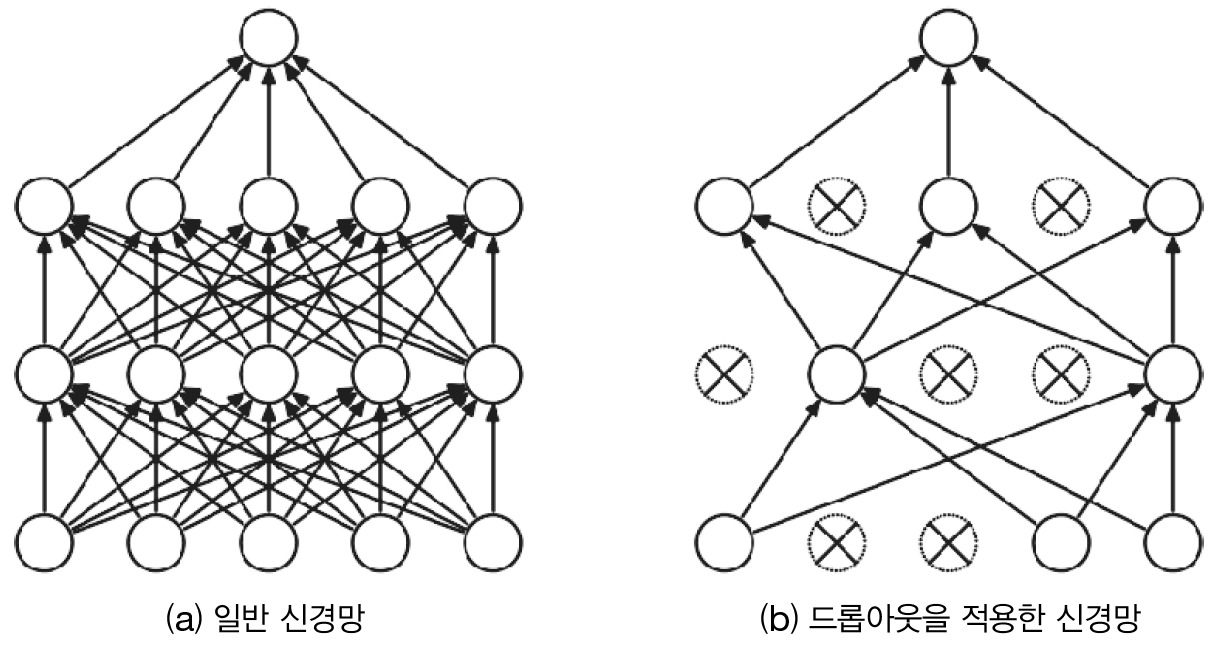
가중치의 초깃값을 적절히 설정하면 각 층의 활성화값 분포가 적당히 퍼지면서 학습이 원활하게 수행됨을 배웠다. 그렇다면 각 층이 활성화를 적당히 퍼뜨리도록 '강제'할 수도 있을까? 실은 배치 정규화(Batch Normalization)가 그런 아이디어에서 출발한 방법이다
9.8장. 딥러닝

이번 포스팅은 딥러닝에 대해서 이야기해보겠다. 딥러닝은 층을 깊게 한 심층 신경망이며, 지금까지 설명한 신경망을 바탕으로 뒷단에 층을 추가하기만 하면 만들 수 있지만, 문제점들을 몇가지 품고 있다. [손글씨 숫자를 인식하는 심층 CNN] 지금까지 구현한 신경망들보다