[Python] 알고리즘 연습 17 (프로그래머스)

N개의 최소공배수 (연습문제)

• 두 수의 최소공배수(Least Common Multiple)란 입력된 두 수의 배수 중 공통이 되는 가장 작은 숫자를 의미합니다. 예를 들어 2와 7의 최소공배수는 14가 됩니다. 정의를 확장해서, n개의 수의 최소공배수는 n 개의 수들의 배수 중 공통이 되는 가장 작은 숫자가 됩니다. n개의 숫자를 담은 배열 arr이 입력되었을 때 이 수들의 최소공배수를 반환하는 함수, solution을 완성해 주세요.

  • 제한사항
    • arr은 길이 1이상, 15이하인 배열입니다.
    • arr의 원소는 100 이하인 자연수입니다.

제출한 코드 :

import math

def lcm(x, y):
    # 두 수의 최소공배수를 계산하는 함수
    return x * y // math.gcd(x, y)

def solution(arr):
    answer = arr[0]
    for num in arr[1:]:
        # answer와 현재 수의 최소공배수를 계산하여 answer에 저장
        answer = lcm(answer, num)
    return answer

---

멀리뛰기 (연습문제)

• 효진이는 멀리 뛰기를 연습하고 있습니다. 효진이는 한번에 1칸, 또는 2칸을 뛸 수 있습니다. 칸이 총 4개 있을 때, 효진이는
  (1칸, 1칸, 1칸, 1칸)
  (1칸, 2칸, 1칸)
  (1칸, 1칸, 2칸)
  (2칸, 1칸, 1칸)
  (2칸, 2칸)
  의 5가지 방법으로 맨 끝 칸에 도달할 수 있습니다. 멀리뛰기에 사용될 칸의 수 n이 주어질 때, 효진이가 끝에 도달하는 방법이 몇 가지인지 알아내, 여기에 1234567를 나눈 나머지를 리턴하는 함수, solution을 완성하세요. 예를 들어 4가 입력된다면, 5를 return하면 됩니다.

  • 제한사항
    • n은 1 이상, 2000 이하인 정수입니다.

제출한 코드 :

def solution(n):
    answer = 0
    a, b = 0,1
    
    for i in range(n) :
        a,b = b, a+b
    
    answer = b % 1234567
    return answer

---

귤 고르기 (연습문제)

• 경화는 과수원에서 귤을 수확했습니다. 경화는 수확한 귤 중 'k'개를 골라 상자 하나에 담아 판매하려고 합니다. 그런데 수확한 귤의 크기가 일정하지 않아 보기에 좋지 않다고 생각한 경화는 귤을 크기별로 분류했을 때 서로 다른 종류의 수를 최소화하고 싶습니다.
  
  예를 들어, 경화가 수확한 귤 8개의 크기가 [1, 3, 2, 5, 4, 5, 2, 3] 이라고 합시다. 경화가 귤 6개를 판매하고 싶다면, 크기가 1, 4인 귤을 제외한 여섯 개의 귤을 상자에 담으면, 귤의 크기의 종류가 2, 3, 5로 총 3가지가 되며 이때가 서로 다른 종류가 최소일 때입니다.
  
  경화가 한 상자에 담으려는 귤의 개수 k와 귤의 크기를 담은 배열 tangerine이 매개변수로 주어집니다. 경화가 귤 k개를 고를 때 크기가 서로 다른 종류의 수의 최솟값을 return 하도록 solution 함수를 작성해주세요.

  • 제한사항
    • 1 ≤ k ≤ tangerine의 길이 ≤ 100,000
    • 1 ≤ tangerine의 원소 ≤ 10,000,000

제출한 코드 :

def solution(k, tangerine):
    answer = 0
    a = {}
    
    for i in tangerine:
        if i in a:
            a[i] += 1
        else:
            a[i] = 1
            
    a = dict(sorted(a.items(), key=lambda x: x[1], reverse=True))
    
    for i in a:
        if k <= 0:
            return answer
        k -= a[i]
        answer += 1
    return answer

---

괄호 회전하기 (월간 코드 챌린지 시즌2)

• 다음 규칙을 지키는 문자열을 올바른 괄호 문자열이라고 정의합니다.
  

  • (), [], {} 는 모두 올바른 괄호 문자열입니다.

  • 만약 A가 올바른 괄호 문자열이라면, (A), [A], {A} 도 올바른 괄호 문자열입니다. 예를 들어, [] 가 올바른 괄호 문자열이므로, ([]) 도 올바른 괄호 문자열입니다.

  • 만약 A, B가 올바른 괄호 문자열이라면, AB 도 올바른 괄호 문자열입니다. 예를 들어, {} 와 ([]) 가 올바른 괄호 문자열이므로, {}([]) 도 올바른 괄호 문자열입니다.
    
    대괄호, 중괄호, 그리고 소괄호로 이루어진 문자열 s가 매개변수로 주어집니다. 이 s를 왼쪽으로 x (0 ≤ x < (s의 길이)) 칸만큼 회전시켰을 때 s가 올바른 괄호 문자열이 되게 하는 x의 개수를 return 하도록 solution 함수를 완성해주세요.

  • 제한사항

    • s의 길이는 1 이상 1,000 이하입니다.

제출한 코드 :

def is_valid(s):
    stack = []
    for char in s:
        if char in ['(', '[', '{']:
            stack.append(char)
        else:
            if not stack:
                return False
            if char == ')' and stack[-1] == '(':
                stack.pop()
            elif char == ']' and stack[-1] == '[':
                stack.pop()
            elif char == '}' and stack[-1] == '{':
                stack.pop()
            else:
                return False
    return len(stack) == 0

def solution(s):
    count = 0
    for i in range(len(s)):
        rotated = s[i:] + s[:i]
        if is_valid(rotated):
            count += 1
    return count

---

연속 부분 수열 합의 개수 (연습문제)

• 철호는 수열을 가지고 놀기 좋아합니다. 어느 날 철호는 어떤 자연수로 이루어진 원형 수열의 연속하는 부분 수열의 합으로 만들 수 있는 수가 모두 몇 가지인지 알아보고 싶어졌습니다. 원형 수열이란 일반적인 수열에서 처음과 끝이 연결된 형태의 수열을 말합니다. 예를 들어 수열 [7, 9, 1, 1, 4] 로 원형 수열을 만들면 다음과 같습니다.
  
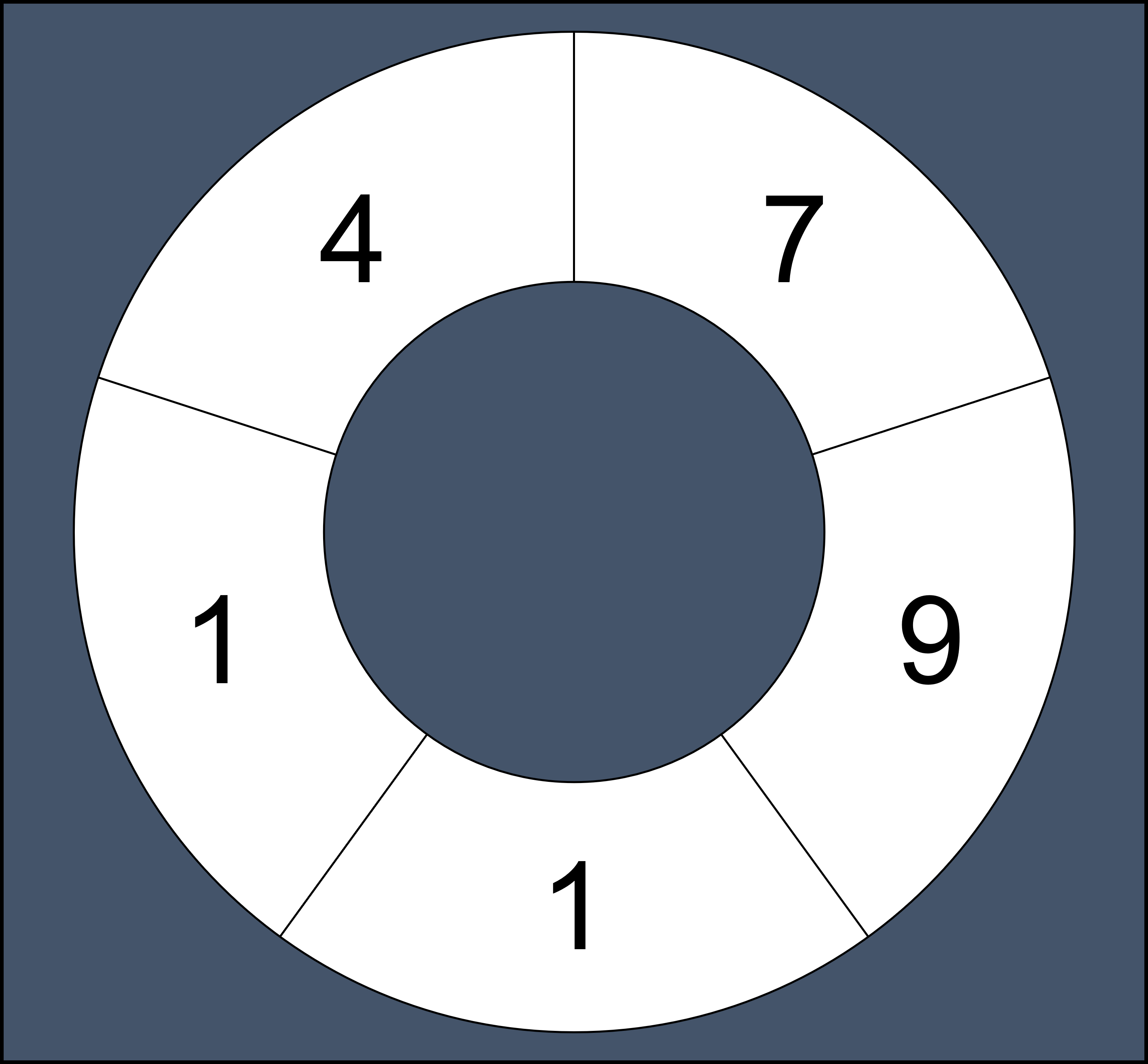
  원형 수열은 처음과 끝이 연결되어 끊기는 부분이 없기 때문에 연속하는 부분 수열도 일반적인 수열보다 많아집니다.
  원형 수열의 모든 원소 elements가 순서대로 주어질 때, 원형 수열의 연속 부분 수열 합으로 만들 수 있는 수의 개수를 return 하도록 solution 함수를 완성해주세요.

  • 제한사항
    • 3 ≤elements의 길이 ≤ 1,000
    • 1 ≤ elements의 원소 ≤ 1,000

제출한 코드 :

def solution(elements):
    n = len(elements)
    total = set()

    for i in range(n):
        s = 0
        for j in range(n):
            s += elements[(i + j) % n]
            total.add(s)

    return len(total)

---