택배 상자 (연습문제)
-
영재는 택배상자를 트럭에 싣는 일을 합니다. 영재가 실어야 하는 택배상자는 크기가 모두 같으며 1번 상자부터 n번 상자까지 번호가 증가하는 순서대로 컨테이너 벨트에 일렬로 놓여 영재에게 전달됩니다. 컨테이너 벨트는 한 방향으로만 진행이 가능해서 벨트에 놓인 순서대로(1번 상자부터) 상자를 내릴 수 있습니다. 하지만 컨테이너 벨트에 놓인 순서대로 택배상자를 내려 바로 트럭에 싣게 되면 택배 기사님이 배달하는 순서와 택배상자가 실려 있는 순서가 맞지 않아 배달에 차질이 생깁니다. 따라서 택배 기사님이 미리 알려준 순서에 맞게 영재가 택배상자를 실어야 합니다.
만약 컨테이너 벨트의 맨 앞에 놓인 상자가 현재 트럭에 실어야 하는 순서가 아니라면 그 상자를 트럭에 실을 순서가 될 때까지 잠시 다른 곳에 보관해야 합니다. 하지만 고객의 물건을 함부로 땅에 둘 수 없어 보조 컨테이너 벨트를 추가로 설치하였습니다. 보조 컨테이너 벨트는 앞 뒤로 이동이 가능하지만 입구 외에 다른 면이 막혀 있어서 맨 앞의 상자만 뺄 수 있습니다(즉, 가장 마지막에 보조 컨테이너 벨트에 보관한 상자부터 꺼내게 됩니다). 보조 컨테이너 벨트를 이용해도 기사님이 원하는 순서대로 상자를 싣지 못 한다면, 더 이상 상자를 싣지 않습니다.
예를 들어, 영재가 5개의 상자를 실어야 하며, 택배 기사님이 알려준 순서가 기존의 컨테이너 벨트에 네 번째, 세 번째, 첫 번째, 두 번째, 다섯 번째 놓인 택배상자 순서인 경우, 영재는 우선 첫 번째, 두 번째, 세 번째 상자를 보조 컨테이너 벨트에 보관합니다. 그 후 네 번째 상자를 트럭에 싣고 보조 컨테이너 벨트에서 세 번째 상자 빼서 트럭에싣습니다. 다음으로 첫 번째 상자를 실어야 하지만 보조 컨테이너 벨트에서는 두 번째 상자를, 기존의 컨테이너 벨트에는 다섯 번째 상자를 꺼낼 수 있기 때문에 더이상의 상자는 실을 수 없습니다. 따라서 트럭에는 2개의 상자만 실리게 됩니다.
택배 기사님이 원하는 상자 순서를 나타내는 정수 배열order가 주어졌을 때, 영재가 몇 개의 상자를 실을 수 있는지 return 하는 solution 함수를 완성하세요.- 제한사항
- 1 ≤
order의 길이 ≤ 1,000,000 order는 1이상order의 길이 이하의 모든 정수가 한번씩 등장합니다.order[i]는 기존의 컨테이너 벨트에order[i]번째 상자를 i+1번째로 트럭에 실어야 함을 의미합니다.
- 1 ≤
- 제한사항
제출한 코드 :
def solution(order):
stack = []
order_idx = 0
n = len(order)
for box in range(1, n + 1):
stack.append(box)
while stack and stack[-1] == order[order_idx]:
stack.pop()
order_idx += 1
return order_idx큰 수 만들기 (탐욕법(Greedy))
-
어떤 숫자에서 k개의 수를 제거했을 때 얻을 수 있는 가장 큰 숫자를 구하려 합니다.
예를 들어, 숫자 1924에서 수 두 개를 제거하면 [19, 12, 14, 92, 94, 24] 를 만들 수 있습니다. 이 중 가장 큰 숫자는 94 입니다.
문자열 형식으로 숫자 number와 제거할 수의 개수 k가 solution 함수의 매개변수로 주어집니다. number에서 k 개의 수를 제거했을 때 만들 수 있는 수 중 가장 큰 숫자를 문자열 형태로 return 하도록 solution 함수를 완성하세요.- 제한사항
- number는 2자리 이상, 1,000,000자리 이하인 숫자입니다.
- k는 1 이상
number의 자릿수미만인 자연수입니다.
- 제한사항
제출한 코드 :
def solution(number, k):
stack = []
for num in number:
while k > 0 and stack and stack[-1] < num:
stack.pop()
k -= 1
stack.append(num)
# k가 남아있는 경우 처리 (남아있는 k만큼 뒤에서 자름)
if k > 0:
stack = stack[:-k]
return ''.join(stack)삼각 달팽이 ()
-
정수 n이 매개변수로 주어집니다. 다음 그림과 같이 밑변의 길이와 높이가 n인 삼각형에서 맨 위 꼭짓점부터 반시계 방향으로 달팽이 채우기를 진행한 후, 첫 행부터 마지막 행까지 모두 순서대로 합친 새로운 배열을 return 하도록 solution 함수를 완성해주세요.
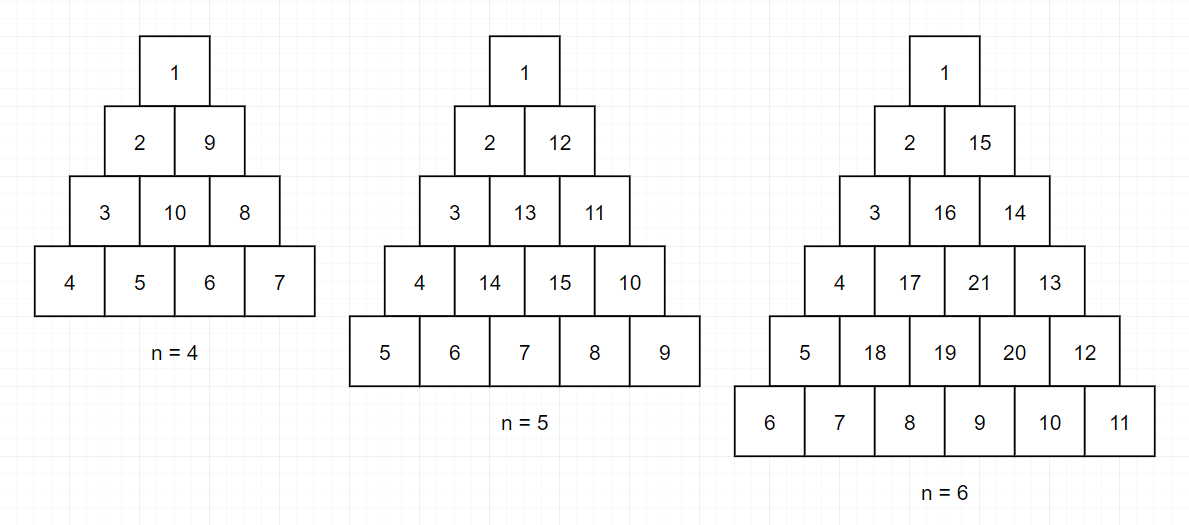
- 제한사항
- n은 1 이상 1,000 이하입니다.
- 제한사항
제출한 코드 :
def solution(n):
# 2차원 배열 초기화
triangle = [[] for _ in range(n)]
# 각 행의 길이 설정
for i in range(n):
triangle[i] = [0] * (i + 1)
# 방향: 아래(0), 오른쪽(1), 위(2)
dx = [1, 0, -1]
dy = [0, 1, -1]
x, y, num = 0, 0, 1
direction = 0
while num <= n * (n + 1) // 2:
triangle[x][y] = num
num += 1
nx, ny = x + dx[direction], y + dy[direction]
if nx < 0 or ny < 0 or nx >= n or ny > nx or triangle[nx][ny] != 0:
direction = (direction + 1) % 3
nx, ny = x + dx[direction], y + dy[direction]
x, y = nx, ny
# 2차원 배열을 일차원 배열로 변환
result = []
for row in triangle:
result.extend(row)
return result연속된 부분 수열의 합 (연습 문제)
-
비내림차순으로 정렬된 수열이 주어질 때, 다음 조건을 만족하는 부분 수열을 찾으려고 합니다.
- 기존 수열에서 임의의 두 인덱스의 원소와 그 사이의 원소를 모두 포함하는 부분 수열이어야 합니다.
- 부분 수열의 합은
k입니다. - 합이
k인 부분 수열이 여러 개인 경우 길이가 짧은 수열을 찾습니다. - 길이가 짧은 수열이 여러 개인 경우 앞쪽(시작 인덱스가 작은)에 나오는 수열을 찾습니다.
수열을 나타내는 정수 배열
sequence와 부분 수열의 합을 나타내는 정수k가 매개변수로 주어질 때, 위 조건을 만족하는 부분 수열의 시작 인덱스와 마지막 인덱스를 배열에 담아 return 하는 solution 함수를 완성해주세요. 이때 수열의 인덱스는 0부터 시작합니다.- 제한사항
- 5 ≤
sequence의 길이 ≤ 1,000,000- 1 ≤
sequence의 원소 ≤ 1,000 sequence는 비내림차순으로 정렬되어 있습니다.
- 1 ≤
- 5 ≤
k≤ 1,000,000,000k는 항상 sequence의 부분 수열로 만들 수 있는 값입니다.
- 5 ≤
제출한 코드 :
def solution(sequence, k):
n = len(sequence)
start, end = 0, 0
current_sum = sequence[0]
min_length = float('inf')
best_range = [0, 0]
while start < n and end < n:
if current_sum == k:
if (end - start) < min_length:
min_length = end - start
best_range = [start, end]
# Move start to reduce the window size
current_sum -= sequence[start]
start += 1
elif current_sum < k:
# Expand the window
end += 1
if end < n:
current_sum += sequence[end]
else:
# Shrink the window
current_sum -= sequence[start]
start += 1
return best_range두 큐 합 같게 만들기 (2022 KAKAO TECH INTERNSHIP)
- 길이가 같은 두 개의 큐가 주어집니다. 하나의 큐를 골라 원소를 추출(pop)하고, 추출된 원소를 다른 큐에 집어넣는(insert) 작업을 통해 각 큐의 원소 합이 같도록 만들려고 합니다. 이때 필요한 작업의 최소 횟수를 구하고자 합니다. 한 번의 pop과 한 번의 insert를 합쳐서 작업을 1회 수행한 것으로 간주합니다.
큐는 먼저 집어넣은 원소가 먼저 나오는 구조입니다. 이 문제에서는 큐를 배열로 표현하며, 원소가 배열 앞쪽에 있을수록 먼저 집어넣은 원소임을 의미합니다. 즉, pop을 하면 배열의 첫 번째 원소가 추출되며, insert를 하면 배열의 끝에 원소가 추가됩니다. 예를 들어 큐 [1, 2, 3, 4]가 주어졌을 때, pop을 하면 맨 앞에 있는 원소 1이 추출되어 [2, 3, 4]가 되며, 이어서 5를 insert하면 [2, 3, 4, 5]가 됩니다.
다음은 두 큐를 나타내는 예시입니다.
queue1 = [3, 2, 7, 2]
queue2 = [4, 6, 5, 1] 두 큐에 담긴 모든 원소의 합은 30입니다. 따라서, 각 큐의 합을 15로
만들어야 합니다. 예를 들어, 다음과 같이 2가지 방법이 있습니다.
1. queue2의 4, 6, 5를 순서대로 추출하여 queue1에 추가한 뒤,
queue1의 3, 2, 7, 2를 순서대로 추출하여 queue2에 추가합니다. 그
결과 queue1은 [4, 6, 5], queue2는 [1, 3, 2, 7, 2]가 되며, 각 큐의 원소
합은 15로 같습니다. 이 방법은 작업을 7번 수행합니다.
2. queue1에서 3을 추출하여 queue2에 추가합니다. 그리고 queue2에서
4를 추출하여 queue1에 추가합니다. 그 결과 queue1은 [2, 7, 2, 4],
queue2는 [6, 5, 1, 3]가 되며, 각 큐의 원소 합은 15로 같습니다. 이
방법은 작업을 2번만 수행하며, 이보다 적은 횟수로 목표를 달성할 수
없습니다.
따라서 각 큐의 원소 합을 같게 만들기 위해 필요한 작업의 최소 횟수는
2입니다.
길이가 같은 두 개의 큐를 나타내는 정수 배열 queue1, queue2가
매개변수로 주어집니다. 각 큐의 원소 합을 같게 만들기 위해 필요한
작업의 최소 횟수를 return 하도록 solution 함수를 완성해주세요. 단,
어떤 방법으로도 각 큐의 원소 합을 같게 만들 수 없는 경우, -1을 return
해주세요.
- 제한사항
- 1 ≤
queue1의 길이 =queue2의 길이 ≤ 300,000 - 1 ≤ `
queue1의 원소,queue2`의 원소 ≤ 109 - 주의: 언어에 따라 합 계산 과정 중 산술 오버플로우 발생 가능성이 있으므로 long type 고려가 필요합니다.
- 1 ≤
제출한 코드 :
def solution(queue1, queue2):
total_sum = sum(queue1) + sum(queue2)
target_sum = total_sum // 2
# 전체 합이 홀수라면 불가능
if total_sum % 2 != 0:
return -1
combined = queue1 + queue2
n = len(queue1)
max_index = len(combined)
start, end = 0, n
current_sum = sum(queue1)
min_operations = float('inf')
while start < max_index and end < max_index:
if current_sum == target_sum:
min_operations = min(min_operations, (start + (end - n)))
current_sum -= combined[start]
start += 1
elif current_sum < target_sum:
if end < max_index:
current_sum += combined[end]
end += 1
else:
break
else:
current_sum -= combined[start]
start += 1
return min_operations if min_operations != float('inf') else -1
