[JAVA] 백준 S1 2293 동전1

출처: 백준 온라인 저지
https://www.acmicpc.net/problem/2293

---

문제 풀이

DP를 이용한 풀이방법이다.
먼저 첫번째 동전만을 사용해서 1~K까지 나타낼 수 있는 경우의 수를 구한다. 동전 한개만 사용하기 때문에 경우의 수는 1만 나올것이다.
다음으로 두번째 동전을 같이 사용하는 경우를 구한다.

예제를 통해 알아보자
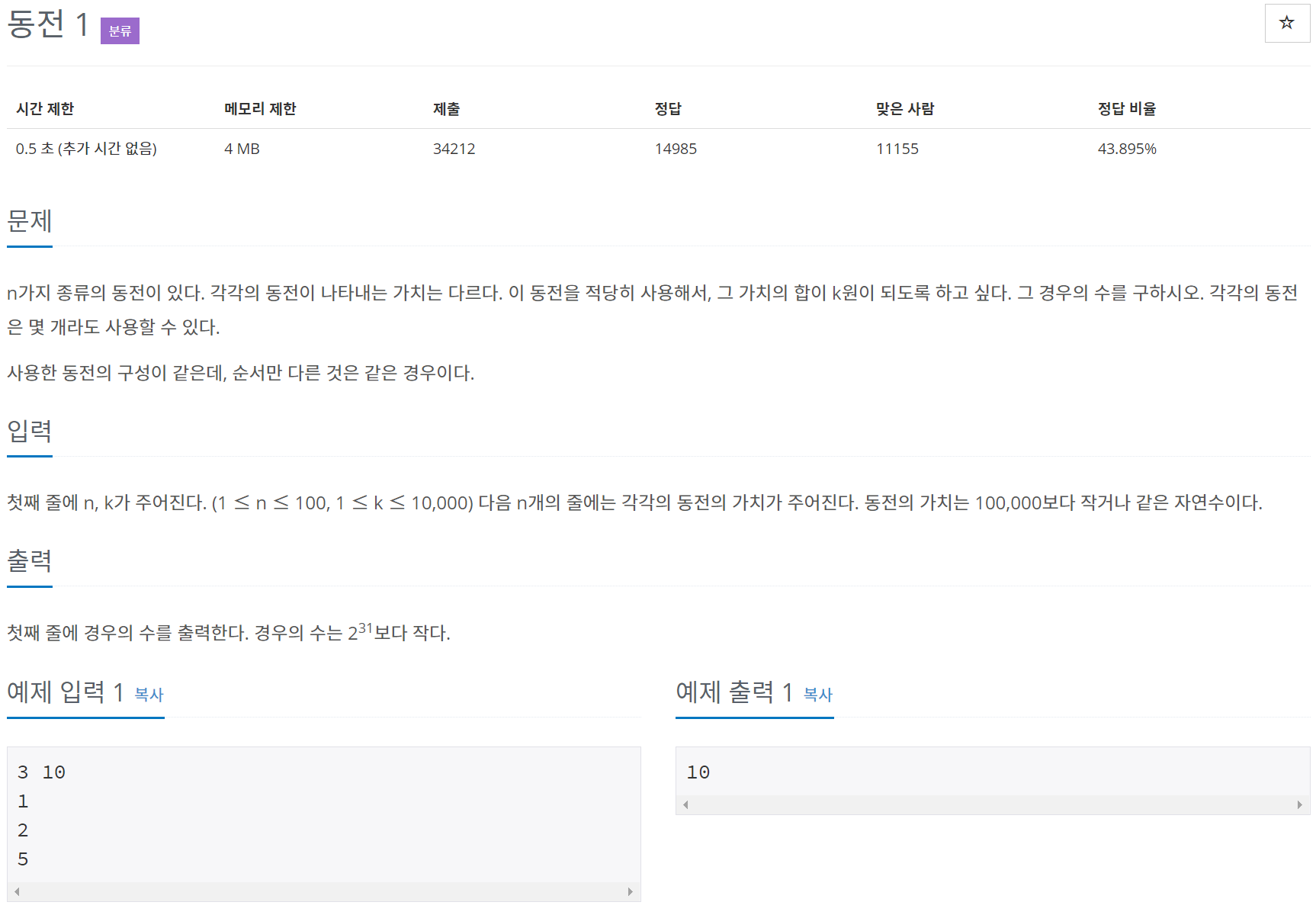
1원 2원 5원 3개의 동전이 있다.

먼저 1원으로만 사용할 경우

	 0 1 2 3 4 5 6 7 8 9 10
1원	 1 1 1 1 1 1 1 1 1 1 1

2원도 같이 사용하는 경우

	 0 1 2 3 4 5 6 7 8 9 10
1원	 1 1 1 1 1 1 1 1 1 1 1
2원	 1 1 2 2 3 3 4 4 5 5 6

3원을 만드는 경우의 수는 (1원으로만 만들 수 있는 경우의 수) + (2원을 사용해서 만들 수 있는 경우의 수)
이는 DP로 나타네면 DP[3] = DP[3] + DP[3 - 2] 로 나타낼수있다.
(1로만 3만드는 경우) + (1로만 1 만드는 경우에 2원동전 하나 추가 == 1로만 1만드는 경우의 수)

동전 하나를 더 추가하면
3원을 만드는 경우의 수는 (1원, 2원으로 만들 수 있는 경우의 수) + (동전을 사용해서 만들 수 있는 경우의 수)

DP에 더 공부해야 겠다...

정답 코드

public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		
		StringTokenizer st = new StringTokenizer(br.readLine());
		
		int N = Integer.parseInt(st.nextToken());
		int K = Integer.parseInt(st.nextToken());
		
		int[] dp = new int[15000];
		int[] arr = new int[N];
		for(int i = 0; i < N; i++) {
			arr[i] = Integer.parseInt(br.readLine());
		}
		dp[0] = 1;
		for(int i = 0; i < N; i++) {
			for(int j = arr[i]; j <= K; j++) {
				dp[j] = dp[j] + dp[j - arr[i]]; 
			}
		}
		System.out.println(dp[K]);
	}