알고리즘 [정수론] - 에라토스테네스의 체

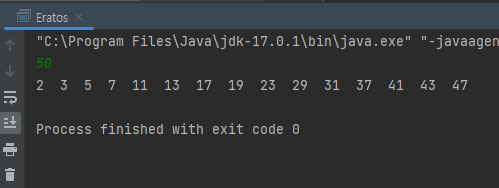
에라토스테네스의 체는 소수를 찾는 방법이다.
고대 그리스 수학자 에라토스테네스가 발견하였다.

---

알고리즘

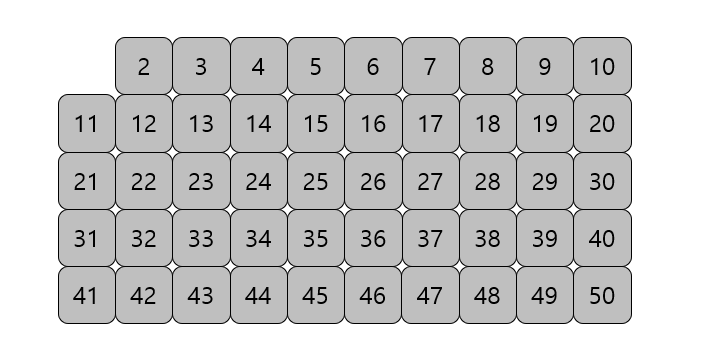
1. 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다.
   그림에서 회색 사각형으로 두른 수들이 여기에 해당된다.
   

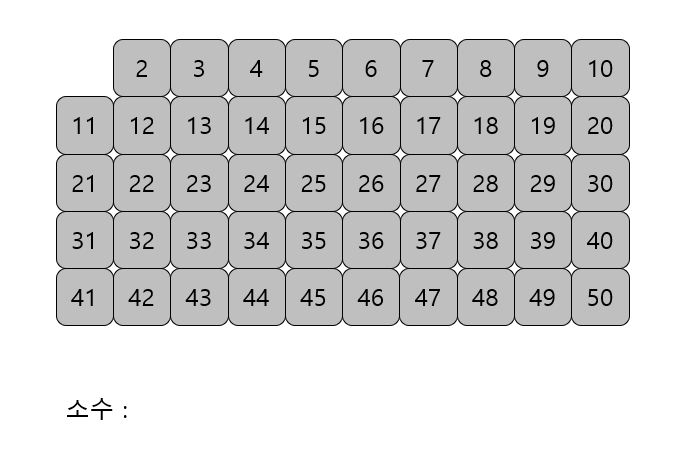
2. 2는 소수이므로 3을 소수로 뺀다.
   

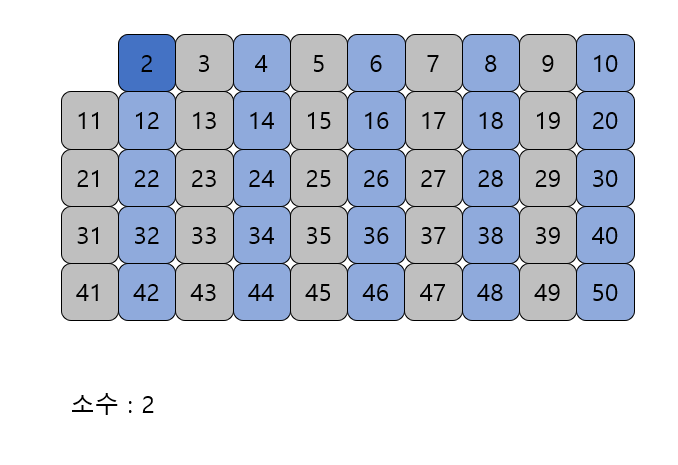
3. 자기 자신을 제외한 2의 배수를 모두 지운다.
   

4. 남아있는 수 가운데 3은 소수이므로 3을 소수로 뺀다.
   

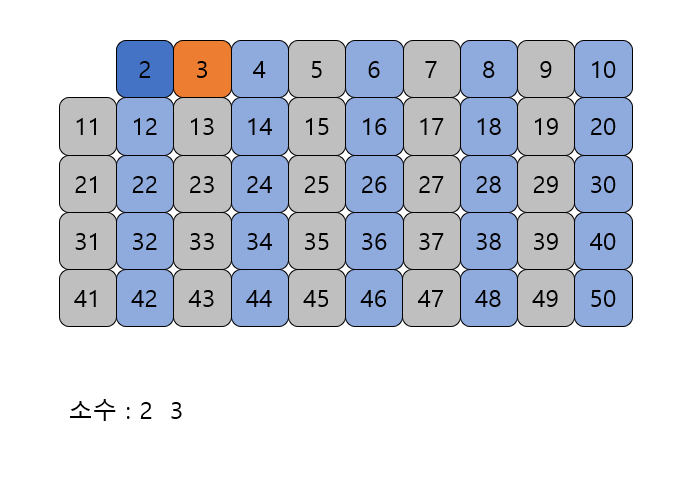
5. 자기 자신을 제외한 3의 배수를 모두 지운다.
   

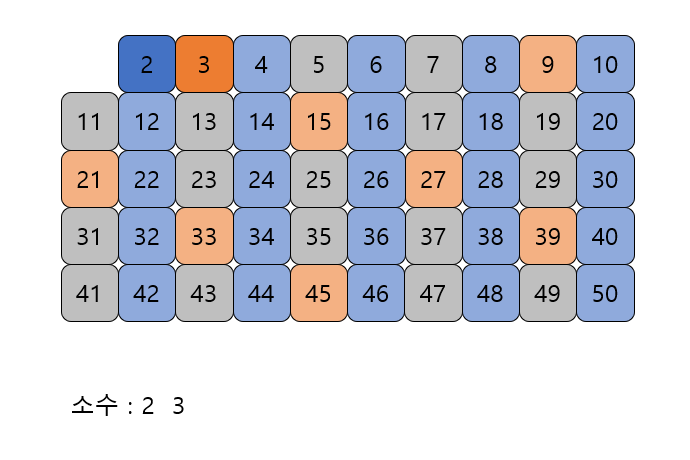
6. 남아있는 수 가운데 5는 소수이므로 5를 소수로 뺀다.
   

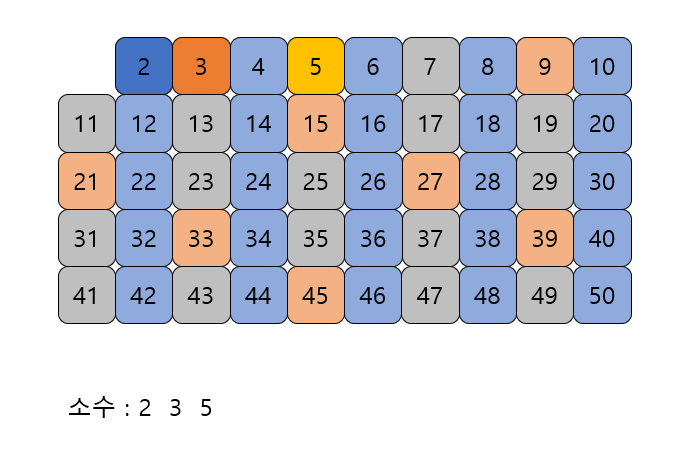
7. 자기 자신을 제외한 5의 배수를 모두 지운다.
   

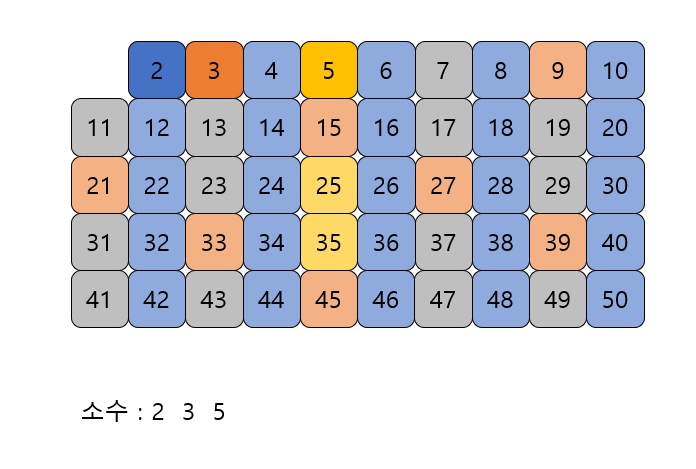
8. 남아있는 수 가운데 7은 소수이므로 7을 소수로 뺀다.
   

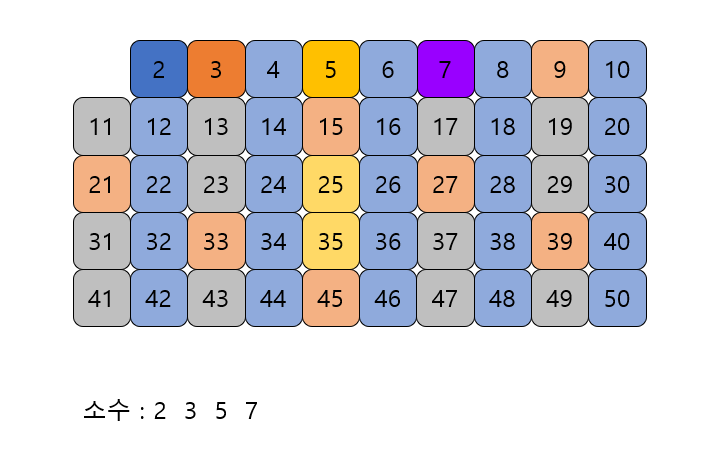
9. 자기 자신을 제외한 7의 배수를 모두 지운다.
   

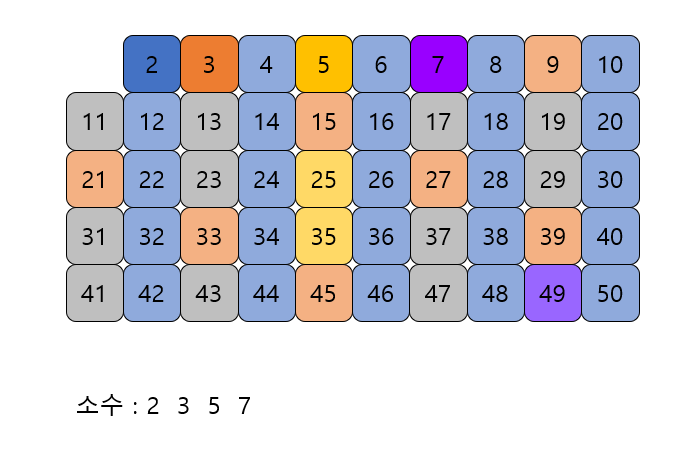
10. 위의 과정을 반복하여 소수를 구한다.
    

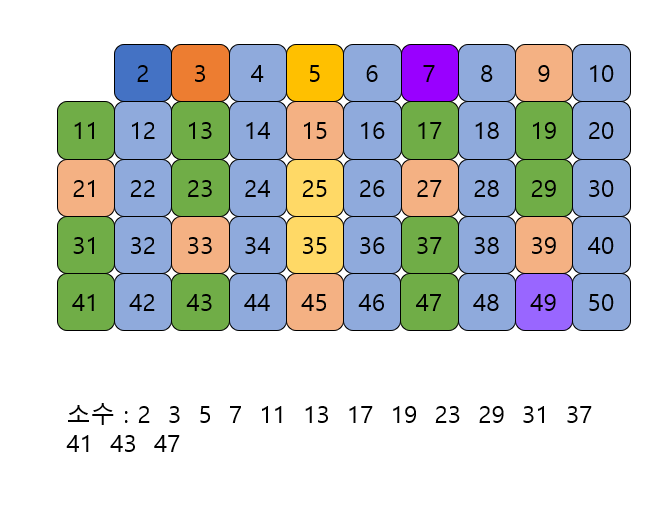
그림의 경우 $8^{2}$ > 50이므로 8보다 작은 수의 배수들만 지워도 충분하다.
즉 50보다 작거나 같은 수 가운데 2, 3, 5, 7의 배수를 지우고 남는 수는 모두 소수이다.

---

Java로 구현

import java.util.ArrayList;
import java.util.Scanner;

public class Eratos {
    public static void main(String[] args){
        ArrayList<Boolean> primeList;   // ArrayList로 구현

        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();

        if(n <= 1)
            return;

        primeList = new ArrayList<Boolean>(n+1);
        // 0번째와 1번째를 소수가 아닌걸로 처리
        primeList.add(false);
        primeList.add(false);

        // 2 ~ n 까지 소수로 설정
        for(int i = 2; i <= n; i++)
            primeList.add(i,true);

        // 2 ~ i*i <= n
        // 각각의 배수들을 지워간다.
        for(int i = 2; (i*i) <= n; i++){
            if(primeList.get(i)){
                for(int j = i*i; j <= n; j+=i)  // i*i 미만은 처리되었으므로 j의 시작값을 i*i로 최적화
                    primeList.set(j, false);
            }
        }

        StringBuffer sb = new StringBuffer();
        for(int i = 0; i <= n; i++){
            if(primeList.get(i) == true){
                sb.append(i);
                sb.append("  ");
            }
        }
        System.out.println(sb.toString());
    }
}