코딩 테스트 [탐색] - 배열에서 k번째 수 찾기

세준이는 크기가 N x N인 배열 A를 만들었다. 배열에 들어 있는 수는 A[i][j] = i x j이다.
이 수를 1차원 배열 B에 넣으면 B의 크기는 N x N이 된다. B를 오름차순으로 정렬했을 때 B[k]를 구하라(배열 A와 B의 인덱스는 1부터 시작한다).

(시간 제한 2초)

---

입력

1번째 줄에 배열의 크기 N이 주어진다. N은 $10^{5}$보다 작거나 같은 자연수다. 2번째 줄에 k가 주어진다. k는 min($10^{9}$, $N^{2}$)보다 작거나 같은 자연수다.

출력

B[k]를 출력한다.

예제 입력
3
7

예제 출력
6

---

1단계 - 문제 분석하기

k의 범위가 1~min($10^{9}$, $N^{2}$) 이므로 시간 복잡도가 $N^{2}$인 알고리즘은 사용할 수 없다. 여기서는 이진 탐색을 사용한다. 이진 탐색으로 중앙값보다 작은 수의 개수를 세면서 범위를 절반씩 줄이는 방법으로 B[k]값을 구한다. 작은 수의 개수가 k-1개인 중앙값이 정답이 된다. 작은 수의 개수를 세는 아이디어가 이 문제를 푸는 열쇠가 된다.

2단계 - 손으로 풀어 보기

2차원 배열은 N행이 N의 배수로 구성되어 있으므로 2차원 배열에서의 k번째 수는 k를 넘지 않는다. 다시 말해 2차원 배열의 1~k번째 안에 정답이 있다. 이점에 주목하여 이진 탐색의 시작 인덱스를 1, 종료 인덱스를 k로 정한다.
다음은 N = 3, k = 7일 때를 예로 들었을 때이다.

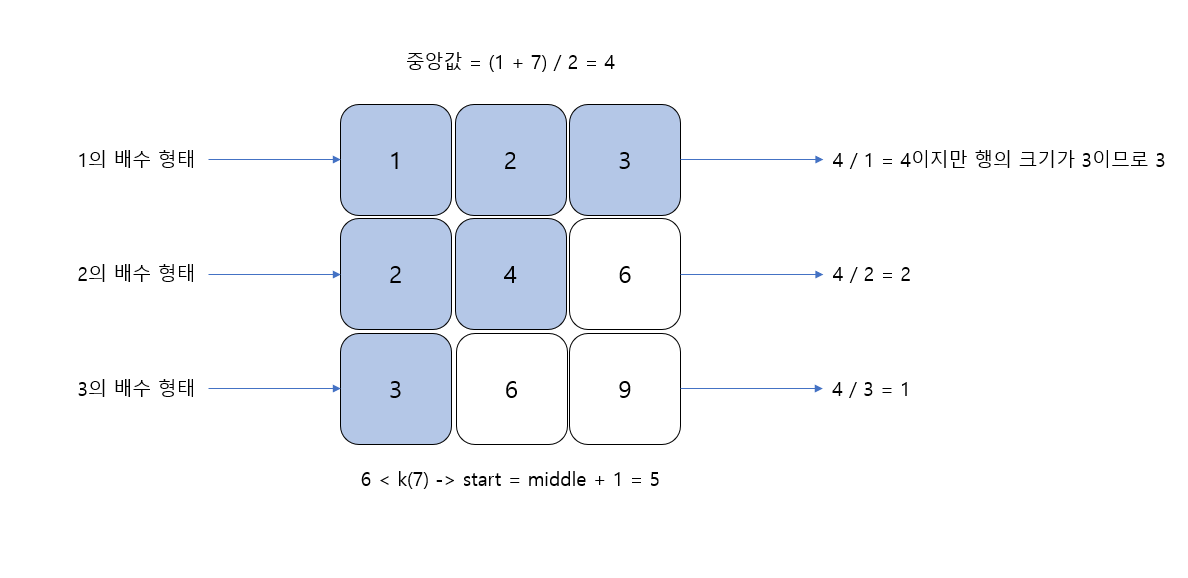
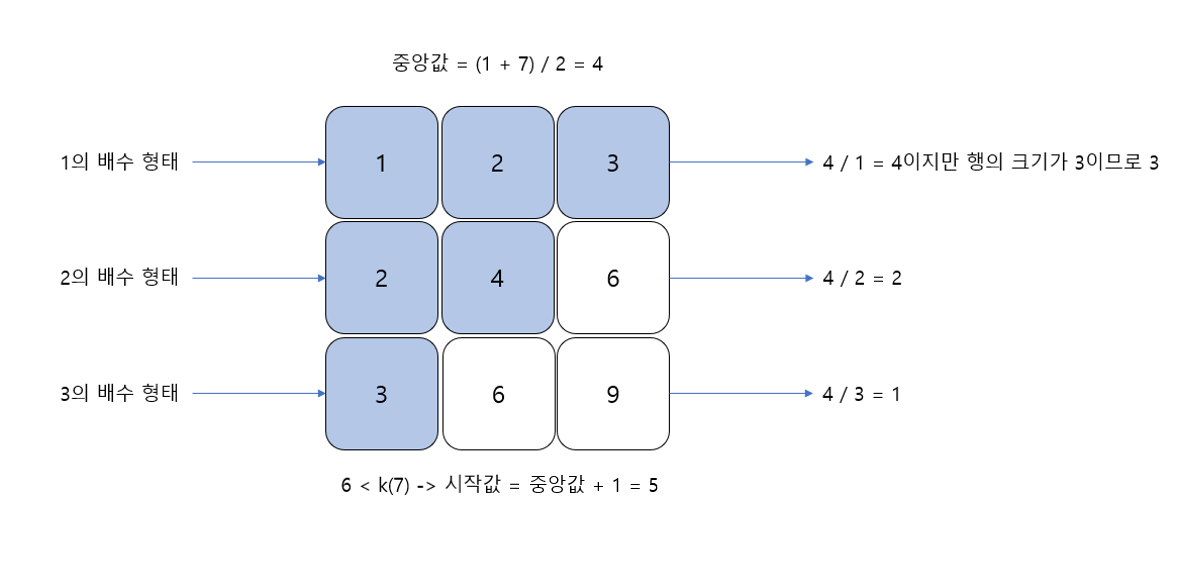
첫 중앙값의 인덱스는 (1+7)/2로 4가 된다.
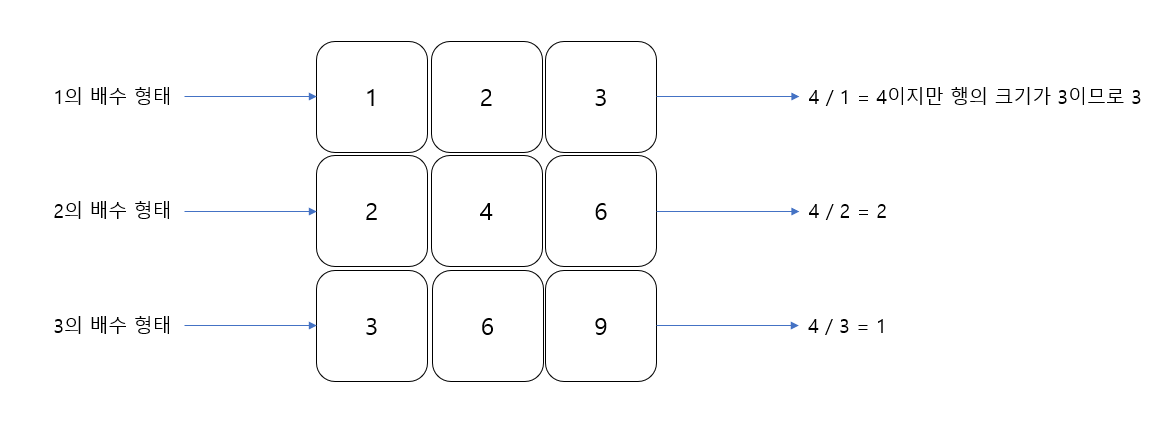
i번째 행에서 중앙값보다 작거나 같은 수의 개수는 중앙값을 i로 나눈 값이다. 단 나눈 값이 N보다 크면 N으로 정한다.
k번째 수가 k를 넘지 않듯이 중앙값보다 작은 수는 중앙값을 넘기지 않는다.
i번째 행은 i의 배수 형태이고, 행 안의 값이 중앙값을 넘지 않으면 중앙값보다 작은 수라는 것이 된다. 그러므로 중앙값을 그 행의 i로 나누어 나온 수가 중앙값의 인덱스를 넘지 않는 수들의 개수가 된다.
식으로 표현하면 Math.min(middle/i, N)이 된다.

결과 중앙값보다 작거나 같은 수의 개수는 3 + 2 + 1 = 6이 된다.

6 < k(7) 이므로, 이를 통해 중앙값 4는 6번째 수보다 큰 수가 될 수 없다는 것을 알 수 있으며, 중앙값 4보다 큰 범위에 정답이 있다는 것을 유추할 수 있다.
그러므로 시작 인덱스를 중앙값+1 로 업데이트하여 이진 탐색을 계속한다.
반대로 중앙값보다 작거나 같은 수의 개수가 k보다 크거나 같으면 종료 인덱스를 중앙값-1 로 업데이트하고, 정답을 중앙값으로 업데이트 한다. 그 후 이진 탐색을 계속한다.

이진 탐색은 시작 인덱스가 종료 인덱스보다 커질때까지 계속하고, 마지막으로 업데이트 한 중앙값이 정답이 된다.

이진 탐색 조건

• 중앙값 크기보다 작은 수가 k보다 작으면 시작 인덱스 = 중앙 인덱스 + 1
• 중앙값 크기가 작은 수가 k보다 크거나 같으면 종료 인덱스 = 중앙 인덱스 - 1, 정답 변수 = 중앙값

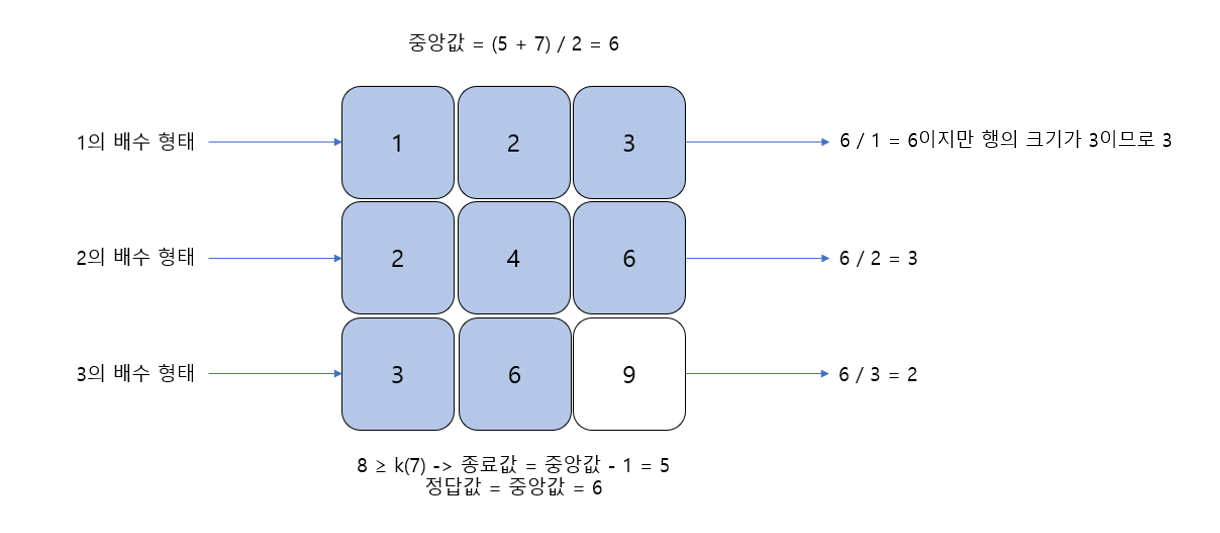
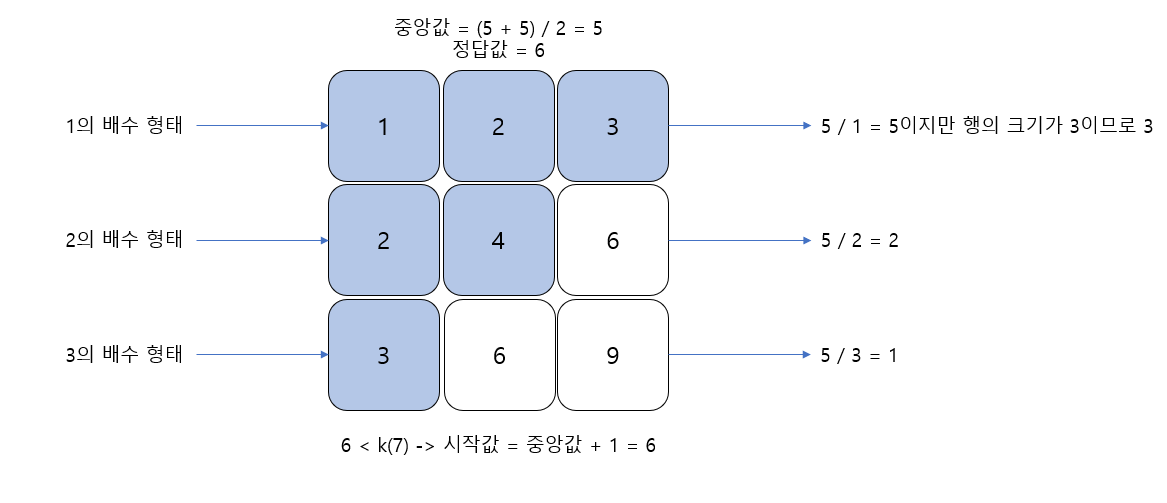
start(6) > end(5) 가 됬으므로 이진 탐색 종료
정답값이 6이므로 정답은 6

3단계 - sudo코드 작성하기

N(배열 크기) k(구하고자 하는 index)
start = 1(시작 인덱스)
end = k(종료 인덱스)

while(시작 인덱스 <= 종료 인덱스)
{
	middle = (시작 인덱스 + 종료 인덱스) / 2
    count(middle보다 작은 수)
    
    for(N만큼 i를 반복)
    {
    	cnt += min(middle/i, N)
    }
    
    if(cnt < k)
    	start = middle + 1
    else
    {
    	end = middle - 1
        정답 변수 = middle
    }
}
정답 변수 출력

4단계 - 코드 구현하기

import java.util.Scanner;

public class Q31 {
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();
        int k = sc.nextInt();

        int start = 1;
        int end = k;
        int answer = 0;

        while(start <= end){
            int mid = (start + end) / 2;
            int count = 0;

            for(int i = 1; i <= N; i++){
                count += Math.min(mid/i, N);
            }

            if(count < k){
                start = mid + 1;
            }else{
                end = mid - 1;
                answer = mid;
            }
        }

        System.out.println(answer);
    }
}

---

• Do it! 알고리즘 코딩테스트 자바 편