[이진 검색 트리]
# 문제
이진 검색 트리는 다음과 같은 세 가지 조건을 만족하는 이진 트리이다.
노드의 왼쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 작다.
노드의 오른쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 크다.
왼쪽, 오른쪽 서브트리도 이진 검색 트리이다.
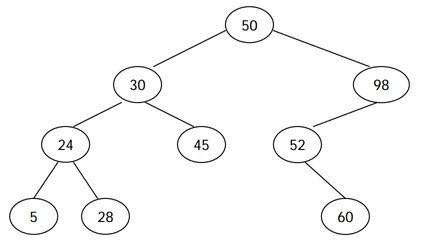
전위 순회 (루트-왼쪽-오른쪽)은 루트를 방문하고, 왼쪽 서브트리, 오른쪽 서브 트리를 순서대로 방문하면서 노드의 키를 출력한다. 후위 순회 (왼쪽-오른쪽-루트)는 왼쪽 서브트리, 오른쪽 서브트리, 루트 노드 순서대로 키를 출력한다. 예를 들어, 위의 이진 검색 트리의 전위 순회 결과는 50 30 24 5 28 45 98 52 60 이고, 후위 순회 결과는 5 28 24 45 30 60 52 98 50 이다.
이진 검색 트리를 전위 순회한 결과가 주어졌을 때, 이 트리를 후위 순회한 결과를 구하는 프로그램을 작성하시오.
# 입력
트리를 전위 순회한 결과가 주어진다. 노드에 들어있는 키의 값은 106보다 작은 양의 정수이다. 모든 값은 한 줄에 하나씩 주어지며, 노드의 수는 10,000개 이하이다. 같은 키를 가지는 노드는 없다.
# 출력
입력으로 주어진 이진 검색 트리를 후위 순회한 결과를 한 줄에 하나씩 출력한다.풀이
0. 풀이 방법
✍️ 한 줄 요약
루트 -> 왼쪽 -> 오른쪽으로 주어지는 입력에서 루트 / 왼쪽 / 오른쪽을 각각 구분해서 왼쪽 -> 오른쪽 -> 루트 순서로 출력해버리쟈💡
문제에서 주어진 예시를 먼저 봅시다잉
루트 노드를 찍은 다음 왼쪽을 싸악 다 돌고 오른쪽을 돌고 있다!
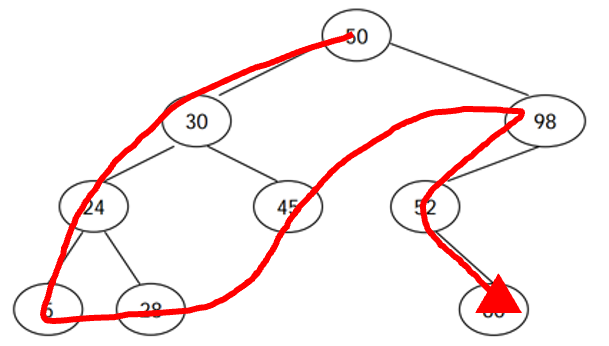

1) 루트는 처음 들어오는 값이니까 당연히 알고
2) 루트보다 작아지면 왼쪽 서브트리
3) 루트보다 커지면 오른쪽 서브트리
이것을 활용해보자 😋
루트 노드

일단, 맨 처음 루트 노드는 50이다. (index는 0)
👉🏻 처음 들어오는 값이 루트 노드임
이 루트 노드 50보다 작은 것들은 왼쪽 서브 트리이고,
50보다 큰 것들은 오른쪽 서브 트리에 해당한다.
왼쪽 서브 트리

50 다음부터 98 전까지 나오는 30, 24, 5, 28, 45는 전부 50보다 작으니
50을 루트로 하는 왼쪽 서브 트리에 해당한다.
이것들의 인덱스는 50의 인덱스 + 1부터 98의 인덱스 -1이다.
처음 루트 노드의 인덱스를 root_idx,
처음으로 루트 노드보다 커진 값의 인덱스를 right_start_idx라고 보면
왼쪽 서브 트리의 인덱스는 루트 다음부터 오른쪽 전까지인
root_idx + 1 ~ right_start_idx - 1이라고 볼 수 있다.
그리고 이렇게 구한 왼쪽 서브 트리의 범위 안에서도 트리가 나눠질 수 있으니
무한 재귀재귀재귀를 돌려줄거당
언제까지? root_idx가 last_idx를 역전하기 전까지(커지기 전까지)!!
오른쪽 서브 트리

왼쪽 서브 트리를 구한 것과 반대로만 생각하면 된다.
50보다 큰 98, 52, 60이 50을 루트로 하는 오른쪽 서브 트리에 해당한다.
이것들의 인덱스는 위에서 구한 right_start_idx부터 마지막까지이다.
마찬가지로 오른쪽 서브 트리의 범위 안에서도 트리가 나눠질 수 있으니
이것들도 무한 재귀를 돌려준다. 인덱스가 역전되기 전까지!
1. 입력 받기
- 입력값의 개수를 안 알려줌 어이없음..
요로케 하면 에러 없이 전체를 입력받을 수 있다.👍🏻
import sys
pre_order = [int(readline) for readline in sys.stdin]2. 최대 재귀 깊이 변경하기
-
재귀 깊이란, 함수가 자기 자신을 호출할 수 있는 최대 깊이로,
파이썬은 기본으로 최대 1000번의 재귀 호출을 허용한다. -
이 문제에서는 기본값으로 두면 이 한계를 초과해서 아래처럼 런타임 에러 (RecursionError)가 발생한다.ㅜㅜ

sys.setrecursionlimit()를 사용해서 최대 재귀 깊이를 늘려주자!
sys.setrecursionlimit(10 ** 6)3. 왼쪽 서브트리와 오른쪽 서브트리가 갈라지는 지점 찾기
-
오른쪽 서브트리와 왼쪽 서브트리를 나누는 구간을 정해주기 위해서
right_start_idx를 찾아야 한다. -
아주 간단하다.
현재의 root보다 값이 커지는 지점의 인덱스를 찾으면 된다. -
오른쪽 서브트리가 시작하는 인덱스를
right_start_idx에 넣어줄 거다.
일단 루트 다음 인덱스를 넣어주고 시작!
right_start_idx = root_idx + 1
while right_start_idx <= last_idx:
if node[right_start_idx] > root:
break
right_start_idx += 1- 처음 루트 노드는 50이니까 노드 98에 해당하는 인덱스 6이
right_start_idx에 들어간다.
4. 각각의 서브트리를 파고들어가 또 서브트리를 찾아준다.
-
계속해서 파고들면, 루트 노드 하나만 남을 때까지 재귀적으로 파고들게 되고,
루트 노드가 되었을 때 출력된다. -
후위 순회한 결과를 출력해야 하므로, 왼쪽 -> 오른쪽 -> 루트 순서로 코드를 배치하면 끝!
# 왼쪽 서브 트리 : 루트의 다음부터 ~ 루트보다 크지 않은 노드까지만
post_order(root_idx + 1, right_start_idx - 1)
# 오른쪽 서브 트리 : 루트보다 큰 노드부터 ~ 끝까지
post_order(right_start_idx, last_idx)
# 루트 출력
print(root)
👆 착실하게 왼쪽 - 오른쪽 - 루트 순서로 잘 파고드는 것을 볼 수 있다 😁
끝!🌲
전체 코드
import sys
sys.setrecursionlimit(10 ** 6)
node = [int(readline.rstrip()) for readline in sys.stdin]
def post_order(root_idx, last_idx):
# 재귀 중단 조건
if root_idx > last_idx:
return
# 루트 노드
root = node[root_idx]
# 오른쪽 서브트리의 시작 인덱스를 담을 변수
right_start_idx = root_idx + 1
while right_start_idx <= last_idx:
# 루트 노드보다 큰 노드의 인덱스를 찾는다.
if node[right_start_idx] > root:
break
right_start_idx += 1
# 왼쪽 서브 트리 : 루트의 다음부터 ~ 루트보다 크지 않은 노드까지만
post_order(root_idx + 1, right_start_idx - 1)
# 오른쪽 서브 트리 : 루트보다 큰 노드부터 ~ 끝까지
post_order(right_start_idx, last_idx)
# 루트 출력
print(root)
post_order(0, len(node) - 1) # 처음과 끝 인덱스를 초기값으로 함수를 호출한다.