알고리즘 유형별 기출문제: 그리디
💻 4. 만들 수 없는 금액
난이도🖤🤍🤍 | 풀이시간 30분 | 제한시간 1초 | 메모리제한 128MB | 2019 카카오 신입 공채 https://programmers.co.kr/learn/courses/30/lessons/42891
📌2021/01/07 작성 코드
(정확성 테스트만 통과한 코드임)
def solution(food_times, k):
answer = 0 # 인덱스 역할을 한다
# 다음 while 문에서 무한 루프에 빠질 가능성 있다...
# 무한 루프에 빠질 가능성, 즉, 모든 음식을 다 먹는 데 걸리는 시간보다 k초가 크면 -1
if sum(food_times) <= k:
return -1
while k > 0:
# 음식이 남아 있음
if food_times[answer] > 0:
food_times[answer] -= 1
k -= 1
answer += 1
# 음식이 남아 있지 않음
else:
answer += 1
# 인덱스 범위 초과 시 적절한 범위로 초기화
if answer >= len(food_times):
answer -= len(food_times)
# k초 동안 먹고 다음에 먹을 인덱스는 현재 answer에 저장되어 있음
# 정상화 후 먹을 음식: food_times[answer] 이므로 유효성을 검증해야한다
# 무한 루프에 빠질 가능성 배제한 뒤의 검증
while food_times[answer] <= 0:
answer += 1
# 인덱스 범위 초과 시 적절한 범위로 초기화
if answer >= len(food_times):
answer -= len(food_times)
return (answer+1) #answer는 인덱스이므로 +1
print(solution([1, 2, 3], 8))
효율성 테스트는 다 나가리였다고.... 도대체 효율성 어떻게 통과하는 걸까?
(효율성 테스트 통과하려고 짰다가 망해버린 코드)
import heapq
def solution(food_times, k):
# 예외: return -1
if sum(food_times) <= k:
return -1
answer = 0
# cycle, remain
cycle = k // len(food_times)
remain = k % len(food_times)
# food_times 내에서 최소 시간
min_time = min(food_times)
# CASE1: 접시를 비울 수 있는 음식이 없을 때
if min_time > cycle:
# answer = (remain + 1)
answer = remain + 1
return answer
# CASE2: 접시를 비울 수 있는 음식이 있을 경우
else:
# 최소 힙을 만든다
heap = []
# food_times의 원소들을 (value, idx)꼴로 최소힙에 옮겨담는다
for i in range(len(food_times)):
heapq.heappush(heap, (food_times[i], i))
# 최소힙에서 cycle보다 작거나 같은 원소를 모두 remove
# cycle을 돈 뒤 접시가 비워지는 원소들을 제거해주는 것
while heap[0][0] <= cycle:
heapq.heappop(heap)
# 최소힙에 남아 있는 원소들 중 remain번째의 인덱스+1이 answer
# 최소힙에 남아 있는 원소들의 idx 기준으로 오름차순으로 정렬
rem_idx = [x[1] for x in heap]
rem_idx.sort()
print("rem_idx:", rem_idx)
# CASE1
if remain < len(rem_idx):
print('case1')
answer = rem_idx[remain] + 1
# CASE2
else:
print('case2')
# 다시 최소 힙 사용하기
heap.clear()
# 최소 힙에 food_times와 rem_idx 이용해 (value, idx) 꼴로 저장
# 이 때 value인 food_times[x] 는 cycle의 값을 빼준 만큼 저장되어 있어야 함
for x in rem_idx:
heapq.heappush(heap, (food_times[x]-cycle,x))
# cycle 값 재할당
cycle = remain // len(rem_idx)
sub_remain = remain % len(rem_idx)
# 최소힙에서 cycle보다 작거나 같은 원소를 모두 remove
# cycle을 돈 뒤 접시가 비워지는 원소들을 제거해주는 것
while heap[0][0] <= cycle:
heapq.heappop(heap)
# rem_idx 초기화
rem_idx.clear()
# 최소힙에 남아 있는 원소들 중 remain번째의 인덱스+1이 answer
# 최소힙에 남아 있는 원소들의 idx 기준으로 오름차순으로 정렬
rem_idx = [x[1] for x in heap]
rem_idx.sort()
# answer
answer = rem_idx[sub_remain] + 1
# answer
return answer
print("6:", solution([5, 7, 1, 3, 4, 2], 6))
print("7:", solution([5, 7, 1, 3, 4, 2], 7))
print("8:", solution([5, 7, 1, 3, 4, 2], 8))
print("9:", solution([5, 7, 1, 3, 4, 2], 9))
print("10:", solution([5, 7, 1, 3, 4, 2], 10))
print("11:", solution([5, 7, 1, 3, 4, 2], 11))
print("12:", solution([5, 7, 1, 3, 4, 2], 12))
print("13:", solution([5, 7, 1, 3, 4, 2], 13))
print("14:", solution([5, 7, 1, 3, 4, 2], 14))
print("15:", solution([5, 7, 1, 3, 4, 2], 15))
print("16:", solution([5, 7, 1, 3, 4, 2], 16))
print("17:", solution([5, 7, 1, 3, 4, 2], 17))
print("18:", solution([5, 7, 1, 3, 4, 2], 18))
💭 아이디어
(1)
정직하게 루프를 돌면서 음식을 먹는 시간을 뺴주고, 음식을 먹는 시간이 0 이하라면 건너뛰는 방식으로 코드를 짰다.
아마 그래서 정확성 테스트는 패스를 했지만 효율성 테스트는 통과를 못했을 것이다.
(2)
그 뒤, 효율성 테스트를 통과하기 위해
몇 번의 cycle을 도는지 k//음식개수 로 계산한 후에
heapq를 이용해 음식을 먹는데 걸리는 시간이 cycle보다 작은 음식은 remove하는 방식으로 코드를 짜보았는데
나머지가 0일 때 꼬여서 정확한 답을 내지 못했다.
🔽결국 해설을 보기로...🔽
🤓 문제 해설
01
이 문제는 시간이 적게 걸리는 음식부터 확인하는 탐욕적(Greedy) 접근 방식으로 해결할 수 있다. 모든 음식을 시간을 기준으로 정렬한 뒤에, 시간이 적게 걸리는 음식부터 제거해 나가는 방식을 이용하면 된다. 이를 위해 우선순위 큐를 이용하여 구현할 수 있는데, 문제를 풀기 위해 고려해야 하는 부분이 많아서 까다로울 수 있다.
02
간단한 예시로 다음과 같이 3개의 음식이 있으며, K를 15초라고 해보자.
- 1번 음식: 8초 소요
- 2번 음식: 6초 소요
- 3번 음식: 4초 소요
🔷 STEP 0
초기 단계에서는 모든 음식을 우선순위 큐(최소 힙)에 삽입한다. 또한 마지막에는 K초 후의 먹어야 할 음식의 번호를 출력해야 하므로 우선순위 큐에 삽입할 때 (음식 시간, 음식 번호)의 튜플 형태로 삽입한다. 그 형태는 아래와 같다.
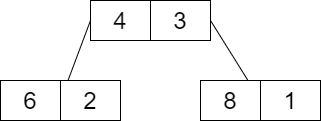
- 전체 남은 시간(K): 15초
- 남은 음식: 3개
🔷 STEP 1
첫 단계에서는 가장 적게 걸리는 음식인 3번 음식을 뺀다. 다만, 음식이 3개 남아있으므로 3(남은 음식의 개수) * 4(3번 음식을 먹는 시간) = 12를 빼야 한다. 다시 말해 3번 음식을 다 먹기 위해서는 12초가 걸린다는 의미이다. 결과적으로 전체 남은 시간이 15초에서 3초로 줄어들게 된다.
.png)
- 전체 남은 시간(K): 3초
- 남은 음식: 2개
- 먹은 음식들:
.png)
🔷 STEP 2
전체 남은 시간은 3초이고, 이번 단계에서는 2번 음식을빼야 한다. 전체 음식이 2개 남아있으므로 이번 단계에서 뺄 시간은 2(남은 음식의 개수) * 2(2번 음식을 다 먹는 시간) = 4초가 된다.
하지만 전체 남은 시간이 3초인데, 이는 4보다 작으므로 빼지 않도록 한다.
따라서 '다음으로 먹어야 할' 음식의 번호를 찾아 출력하면 된다. 다음 그림처럼 매초 먹어야 할 음식들을 일렬로 나열해보자. 전체 남은 시간이 3초이므로, 4번쨰 음식의 번호를 출력하면 정답이다.
.png)
- 전체 남은 시간(K): 3초
- 남은 음식: 2개
따라서 2번 음식을 출력한다.
03
소스코드는 다음과 같은데, 필자는 우선순위 큐를 구현하기 위해서 heapq를 이용했다. 우선순위 큐에 대한 내용은 다익스트라 알고리즘 파트에서 다루었으니, 여기에서 추가로 언급하지는 않겠다.
🤓 답안 예시
import heapq
def solution(food_times, k):
# 전체 음식을 먹는 시간보다 k가 크거나 같다면 -1
if sum(food_times) <= k:
return -1
# 시간이 작은 음식부터 빼야 하므로 우선순위 큐를 이용
q = []
for i in range(len(food_times)):
# (음식 시간, 음식 번호) 형태로 우선순위 큐에 삽입
heapq.heappush(q, (food_times[i], i + 1))
sum_value = 0 # 먹기 위해 사용한 시간
previous = 0 # 직전에 다 먹은 음식 시간
length = len(food_times) # 남은 음식의 개수
# sum_value + (현재의 음식 시간 - 이전 음식 시간) * 현재 음식 개수와 k 비교
while sum_value + ((q[0][0] - previous) * length) <= k:
now = heapq.heappop(q)[0]
sum_value += (now - previous) * length
length -= 1 # 다 먹은 음식 제외
previous = now # 이전 음식 시간 재설정
# 남은 음식 중에서 몇 번째 음식인지 확인하여 출력
result = sorted(q, key=lambda x: x[1]) # 음식의 번호 기준으로 정렬
return result[(k - sum_value) % length][1]오 sum_value의 값을 업데이트 해주는 게 핵심
sum_value + ☆(현재의 음식 시간 - 이전 음식 시간) * 현재 음식 개수☆와 k 비교
while문의 컨디션은 즉, 이전 음식을 먹어치운 뒤, 현재의 음식도 먹어치울 수 있을것인가를 판단하는 것이 된다.
🤔 리뷰
- 카카오 코테 치고는 쉬워보였으나 효율성 테스트를 통과하기가 어려웠다.
- 효율성 테스트에서 우선순위큐를 이용해야 한다는 아이디어까지는 도달했지만, 내 알고리즘으로는 정확한 답이 나오지 않았다.
- 카카오 코테에서는 정확성, 효율성 모두 만족시켜야 한다는 것을 깨달았음.
- Python의 lambda란?? (답안 예시 마지막 line)
+) 람다 표현식(lambda express)
함수를 간단하게 작성하여 적용할 수 있게 함. 특정 기능을 수행하는 함수를 한 줄에 작성할 수 있다는 것이 특징.
def add(a, b):
return a + b
# 일반적인 add() 메서드 사용
print(add(3, 7))
# 람다 표현식으로 구현한 add() 메서드
print((lambda a, b: a+ b)(3, 7))파이썬의 정렬 라이브러리를 사용할 때, 정렬 기준인 key를 설정할 때에도 자주 사용된다.
