🥚문제

https://www.acmicpc.net/problem/1915

• 다이나믹 프로그래밍

---

🥚입력/출력

---

🍳코드

import sys
input = sys.stdin.readline

n, m = map(int, input().split())
arr = [[0]*(m+1)] + [[0] + list(map(int, list(input().strip())))
                     for _ in range(n)]

# dp[r][c] = 우측 하단 꼭짓점이 (r,c)인 영역 내의 정사각형의 최대 변의 길이
# 정사각형이 될 수 없을 때는 0으로 표시
dp = [[0]*(m+1) for _ in range(n+1)]

for r in range(1, n+1):
    for c in range(1, m+1):
        if r == 1 or c == 1:
            dp[r][c] = arr[r][c]

        elif arr[r][c] == 0:
            dp[r][c] = 0

        else:  # arr[r][c] == 1
            dp[r][c] = min(dp[r-1][c], dp[r-1][c-1], dp[r][c-1]) + 1

ans = max(map(max, dp))
print(ans**2)

---

🧂아이디어

DP

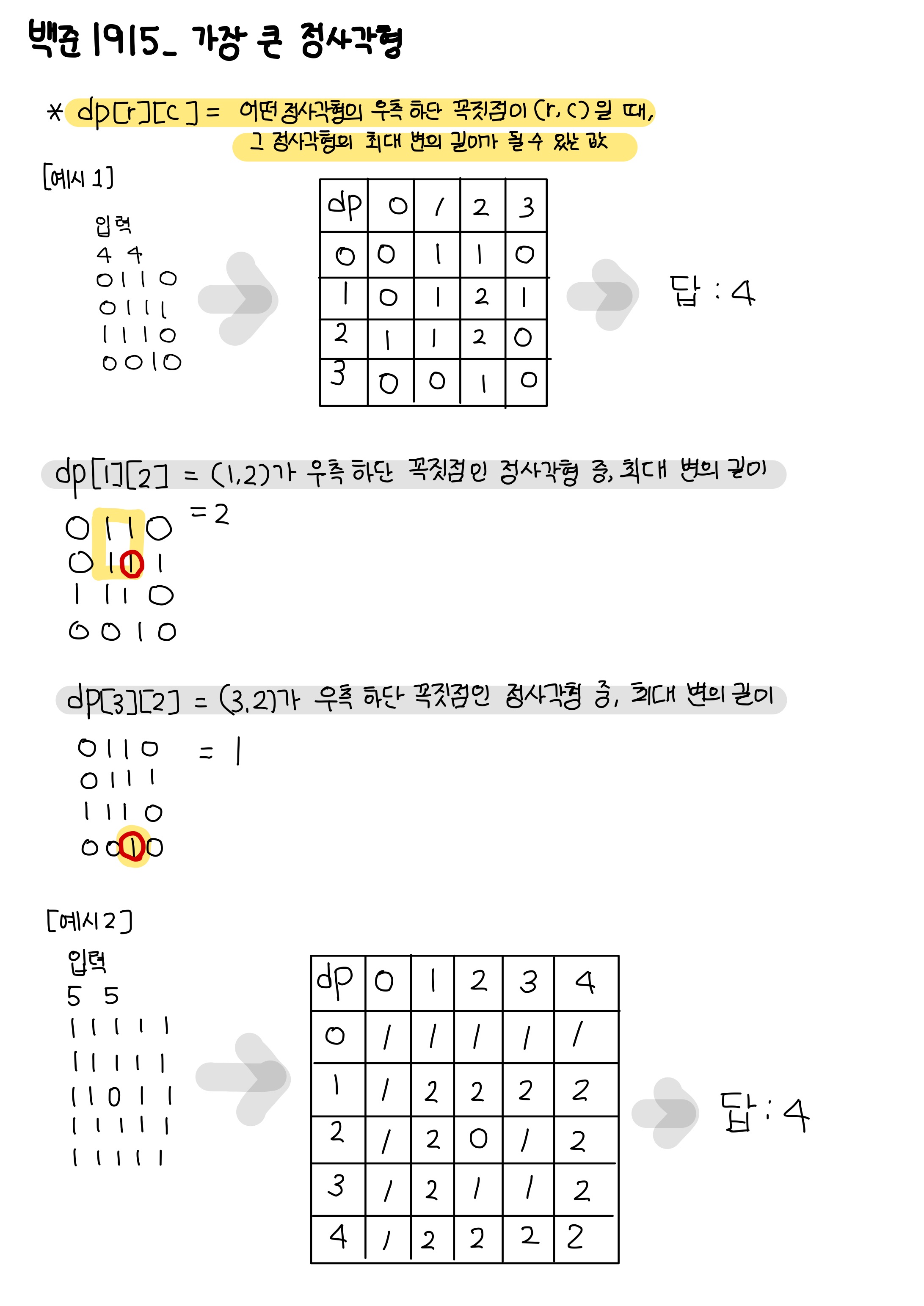
• dp[r][c] = 어떤 정사각형의 우측 하단 꼭짓점이 (r, c)일 때, 그 정사각형의 최대 변의 길이가 될 수 있는 값

• 입력으로 주어진 N*M 배열을 순회하며 dp값을 갱신한다.

• dp[r][c]의 값을 갱신할 때, r == 0 또는 c == 0이면 dp[r][c] = arr[r][c]

• arr[r][c] == 0이면 (r,c)를 우측 하단 꼭짓점으로 갖는 정사각형이 만들어지지 않으므로 dp[r][c] = 0

• arr[r][c] == 1이면 (r, c)를 우측 하단 꼭짓점으로 갖는 정사각형의 최대 변의 길이는 min(arr[r-1][c-1], arr[r-1][c], arr[r][c-1]) + 1

• 답을 출력할 때는, 2차원 리스트 dp의 최대값에 제곱한 값을 출력하면 된다.

참고: https://kyun2da.github.io/2021/04/09/biggestSquare/