[알고리즘] 최단 경로 - 다익스트라 알고리즘

최단 경로 알고리즘은 말 그대로

가장 짧은 경로를 찾는 알고리즘 입니다 😄

다양한 종류의 최단 경로 문제가 있는데

각각의 상황에 맞는 효율적인 알고리즘은 이미 정립되어 있다고 하네요


최단 경로는 문제는 보통 그래프를 이용하는데

그럼 그래프는 뭘까요?

그래프

그래프는 노드 또는 정점(vertex)과 이를 연결하는 간선(edge)으로 구성됩니다

그래프의 종류

• 무향 그래프 (방향 x)
• 유향 그래프 (방향 o)
• 가중치 그래프
  ...

등 다양한 종류가 존재합니다

트리 또한 사이클이 없는 무향 그래프로 볼 수 있습니다


이러한 그래프에서 최단 거리는

시작 노드에서 목표 노드까지 도달하는데

간선의 가중치의 합이 최소가 되는 경로를 말합니다


이러한 문제를 해결하기 위한 최단 거리 알고리즘으로

크게 3가지 알고리즘이 존재합니다

• 다익스트라
• 플로이드 워셜
• 벨만 포드

이 중에서 가장 많이 알려진 다익스트라 알고리즘에 대해서 알아보겠습니다

다익스트라 알고리즘

다익스트라 알고리즘은 음의 가중치가 존재하지 않을 때 정상적으로 작동합니다

차량 네비게이션에 실제로 사용되는 알고리즘이라고 합니다

다익스트라 알고리즘은 그리디 알고리즘 및 다이나믹 프로그래밍의 한 유형으로 볼 수 있습니다

매번 가중치가 가장 적은 노드를 선택해서 임의의 과정을 반복하기 때문입니다

1. 초기화
   : 시작 정점에서 다른 모든 정점까지의 거리를 무한대로 설정하고, 시작 정점의 거리는 0으로 설정

2. 정점 선택
   : 방문하지 않은 정점 중에서 시작 정점으로부터 가장 짧은 거리를 가진 정점을 선택

3. 거리 갱신
   : 선택한 정점을 통해 다른 인접한 정점으로 가는 경로를 탐색하고
   기존에 기록된 거리보다 짧으면 갱신

4. 반복: 모든 정점을 방문할 때까지 2번과 3번 과정을 반복

풀이

다음과 같은 그래프가 있다고 가정해봅시다

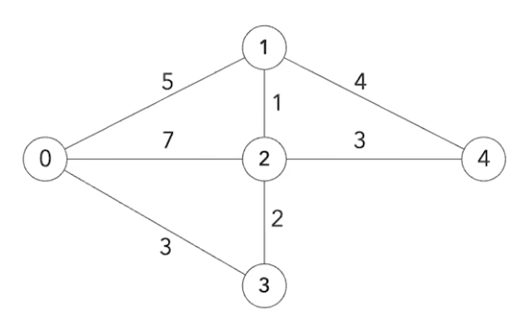
노드 0에서 출발한다고 하면

노드번호	0	1	2	3	4
거리	0	무한	무한	무한	무한

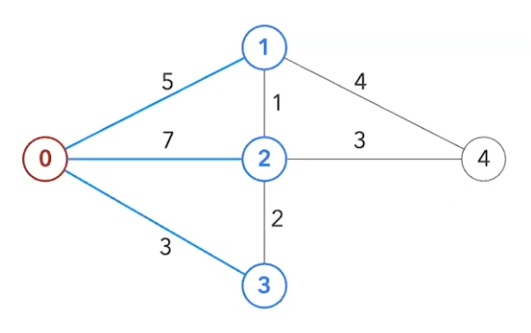
인접한 노드는 1, 2, 3이 있는데

각각의 노드로 가는 거리를 계산합니다

• 1 → 5
• 2 → 7
• 3 → 3

계산한 거리를 바탕으로 테이블을 갱신하면

노드번호	0	1	2	3	4
거리	0	5	7	3	무한

인접한 노드 중 거리가 최소인 노드는 3입니다

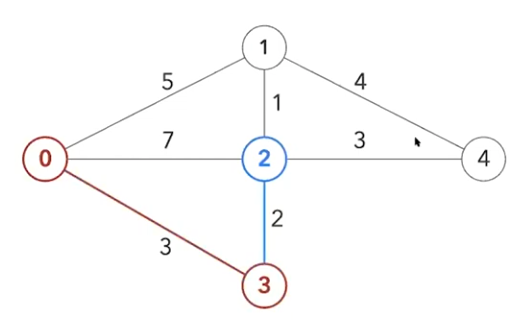
3에서 갈 수 있는 곳은 2인데

처음에 0에서 2로 가는 거리인 7과 비교했을 때

3을 통해 2 가면 거리가 5로 더 짧죠?

바로 테이블을 갱신해줍니다

노드번호	0	1	2	3	4
거리	0	5	5	3	무한

그 다음으로 거리가 최소인 정점 1로 가봅시다

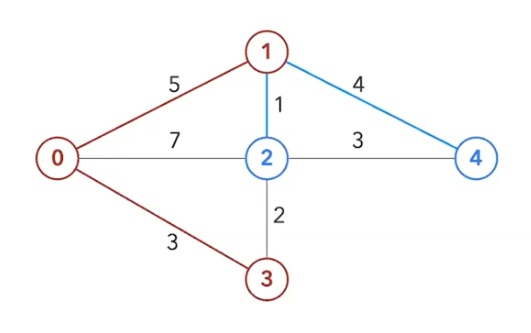
1에서 갈 수 있는 곳은 2와 4가 있죠

또 거리를 계산해봅시다

• 2 → 6
• 4 → 9

다시 테이블 갱신!

노드번호	0	1	2	3	4
거리	0	5	5	3	9

다음으로 이번엔 2를 방문해서

방문하지 않았던 4로 가봅시다

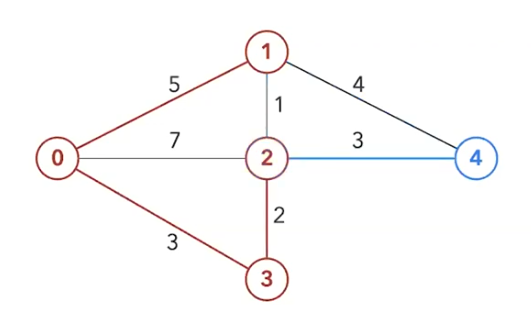
다시 거리 계산 후 테이블 갱신이겠죠?

• 4 → 5 + 3 = 8

노드번호	0	1	2	3	4
거리	0	5	5	3	8

이러한 과정을 통해 최단 경로를 구할 수 있습니다!


결과적으로

다익스트라 알고리즘이 진행되면서

한 단계당 하나의 노드에 대한 최단 거리를 확실히 찾는 것으로 이해할 수 있습니다

그렇기 때문에 위의 설명에서 한 것처럼

마지막 노드에 대해서는 따로 확인할 필요가 없습니다

이미 나머지 노드에 대해서 최단 거리가 확정된 상태이기 때문입니다

출처

[10분 테코톡] 💞 소롱의 최단 경로 & 최소 신장 트리
이것이 취업을 위한 코딩 테스트다 with 파이썬