TIL-시간복잡도

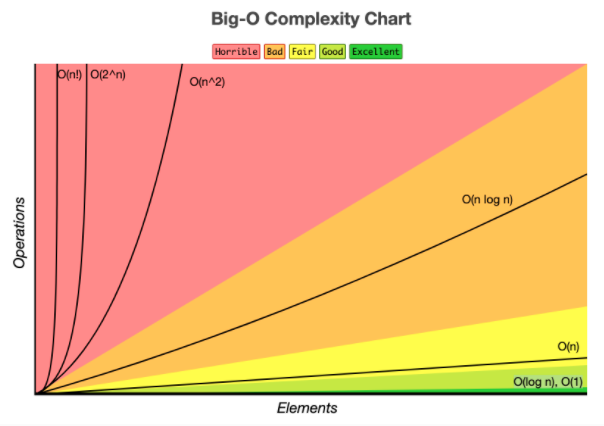
Time Complexity

• 알고리즘 문제의 효율적인 방법 또는 코드를 고민하는 것은 시간복잡도를 고민하는 것과 같은 말

• 시간복잡도의 표기법

  • Big-O(빅-오): 최악의 경우, 가장 자주 사용됨
    • 최선이나 평균을 기대하는 것보다, 최악의 경우를 대비하는 것이 바람직함
  • Big-Ω(빅-오메가): 최선의 경우
  • Big-θ(빅-세타): 중간(평균)의 경우

• Big-O 표기법의 종류

  • O(1): constant complexity, 입력값의 크기에 상관없이, 즉시 출력값을 얻어 낼 수 있음
    • (ex) const a = (arr, idx) => {return arr[idx]}
    • arr가 아무리 커져도 정해진 idx를 반환하고 종료된다
  • O(n): linear complexity, 입력값에 따라 시간이 같은 비율로 증가하는 것
    • for(let i=0; i<n; i++) or for(let i=0; i<2n; i++) {console.log(i)}
    • 앞의 경우 0부터 n-1까지 n의 입력값이 비례하여 실행됨, 뒤의 경우 O(2n)으로 볼 수도 있지만, 저러한 경우도 O(n)으로 표기한다
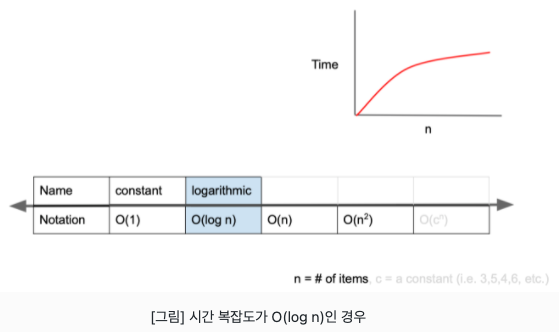
  • O(log n): logarithmic complexity, O(1) 다음으로 빠른 시간복잡도를 가진다
    • BST가 대표적 예, 노드를 이동할 때마다 경우의 수가 절반으로 줄어듬
    • 게임에 비유하자면, UP&DOWN을 예로 들 수 있음
      
  • O(n^2): quadratic complexity, 입력값의 증가에 시간이 n의 제곱수의 비율로 증가
    • (ex) const b = (n) => {for(let i=0; i<n; i++) {for(let j=0; j<n; j++) {console.log(i)}}}, 3,4중반복문도 마찬가지
    • 2n,3n을 O(n)으로 표기하는 것과 같이, n^3, n^5도 O(n^2)로 표기함
  • O(2^n): exponential complexity, Big-O 중 가장 느린 시간복잡도
    • 재귀로 구현하는 피보나치 수열이 대표적인 예
    • const fibo =(n)=>{if(n <= 1) {return 1;} return fibo(n-1)+fibo(n-2)}

• 데이터 크기에 따른 시간복잡도

  • 코딩테스트에서 주어지는 데이터 크기 제한에 따른 예상 시간복잡도를 계산하여 프로그램을 계산하면 쉬운 계산법으로 풀 수 있는 것을, 굳이 어려운 방법으로 풀려고 애쓸 필요가 없어짐
  • 즉, 입력 데이터가 클 때는 O(n), O(log n)의 시간복잡도를 만족할 수 있도록 예측해서 풀어야 하고, 주어진 데이터가 작을 때에는 시간복잡도가 크더라도 문제를 풀어내는 것에 집중해야 함

• 대략적인 데이터 크기에 따른 시간복잡도

  데이터 크기 제한	예상되는 시간복잡도
  n ≤ 1,000,000	O(n) or O(log n)
  n ≤ 10,000	O(n^2)
  n ≤ 500	O(n^3)