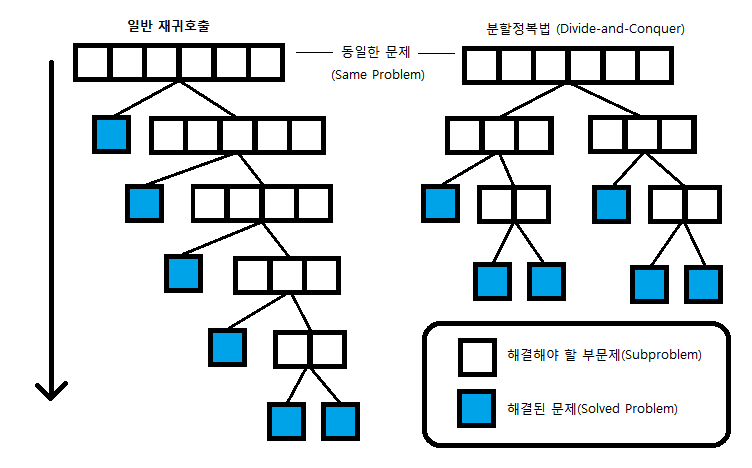
지난번에 정리한 백트레킹에 이어 한번 날잡고 제대로 공부해야겠다고 마음먹은 분할정복이다. 간혹가다가 분할정복 문제를 접하게 되면 그 매커니즘이 직관적으로는 이해되지만 100% 내것이다!라고 말하기엔 애매한 부분들이 좀 많은 것 같아, 제대로 개념 정리 후, 관련 문제들을 풀어보고자 한다. 그럼 우선 분할정복의 개념부터 알아보자!
분할정복
주어진 문제를 둘 이상의 부분 문제로 나눈 뒤 각 문제에 대한 답을 재귀 호출을 이용해 계산, 각 부분 문제의 답으로부터 전체 문제의 답을 계산해내는 방식이다.
여기까지만 읽어보면 Dynamic Programming과 비슷하네?라는 생각이 들었다. 문제를 잘게 조개서, 작은 단위부터 분할해 접근한다는 점은 비슷하지만, DP와 분할정복에는 큰 차이가 있다.
DP(동적 계획법)
- 해결한 부분 문제들이 중복되어, 상위 문제 해결시 재활용
- Memoization 기법(DP table)등등 사용
분할정복
- 부분 문제가 서로 중복되지 않으며,
- Memoization 기법 역시 사용하지 않는다고 한다.
그럼, 이어서 분할정복의 추가적인 특징들을 정리해보도록 하자.
- 문제를 둘 이상의 부분 분제로 나누는 자연스러운 방법이 있어야 함
- 부분 문제의 답을 조합해 원래 문제의 답을 계산하는 효율적인 방법이 있어야 함
이라고 한다. 어느정도 개념에 대한 대략적인 감이 잡혔으니 본격적으로 문제를 풀어보며 분할정복을 정복해보자!
백준 1629 곱셈
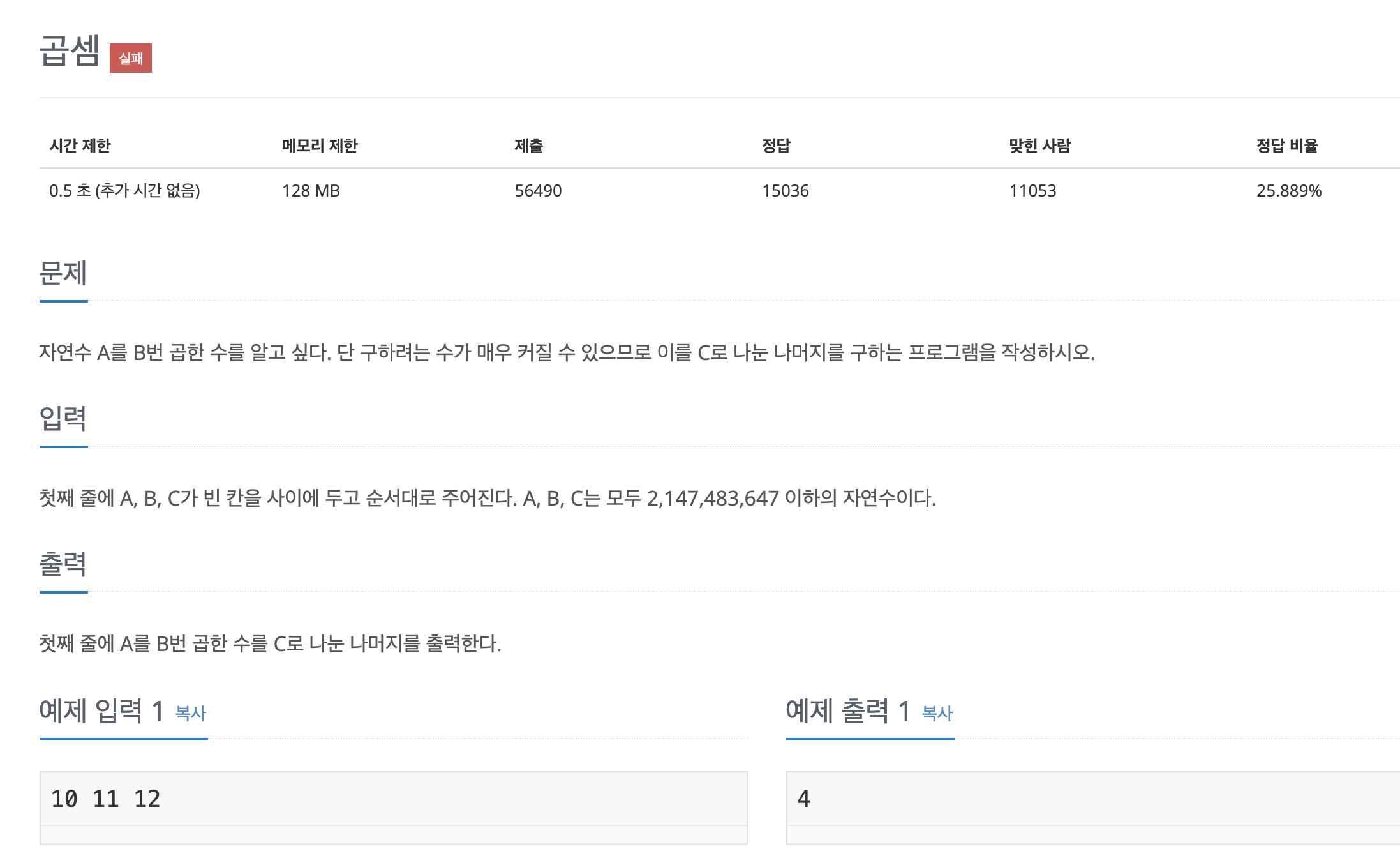
첫번째 분할정복을 이용한 문제는 자연수 A의 B승을 C로 나눈 나머지를 구하는 문제이다. 처음에는 ㅇㅡㅇ? 하고
import math
a, b, c = map(int, input().split())
print(int(math.pow(a,b) % 12))이렇게 간단한 문젠가?라고 생각했다가 보기좋게

런타임 에러가 떨어졌다. 이 문제를 해결하는 키는 바로 '분할정복'을 이용하는 것이다. 구체적인 매커니즘은 다음과 같다.
무식한 제곱의 연산 과정을 단순화 하기 위해선 나머지 분배 법칙과 지수법칙을 알아야 한다고 한다.
- 지수 법칙
A^m+n = A^m x A^n
- 나머지 분배 법칙
(AxB)%C = (A%C) *(B%C) % C
이 문제의 예제에 적용을 해보면
a = 10 , b = 11 , c = 12
10^11 % 12
= ((10^5)%12 x (10^5)%12 x 10)% 12
= ((10^2)%12 x (10^2)%12 x 10) %12 x (10^2)%12 x (10^2)%12 x 10) %12 x 10) %12
으로 곱셈을 계속해서 분할해 나갈 수 있다.
import sys
a,b,c = map(int,sys.stdin.readline().split())
def multi (a,n):
if n == 1:
return a%c
else:
tmp = multi(a,n//2)
if n %2 ==0:
return (tmp * tmp) % c
else:
return (tmp * tmp *a) %c
print(multi(a,b))분할정복의 개념을 와닿게 이해할 수 있는 좋은 문제였지만.. 사실 위의 공식을 알고 있지 않다면, 거의 풀 수 없을 문제가 아닌가..라고 생각이 든다.
백준 1780: 종이의 개수
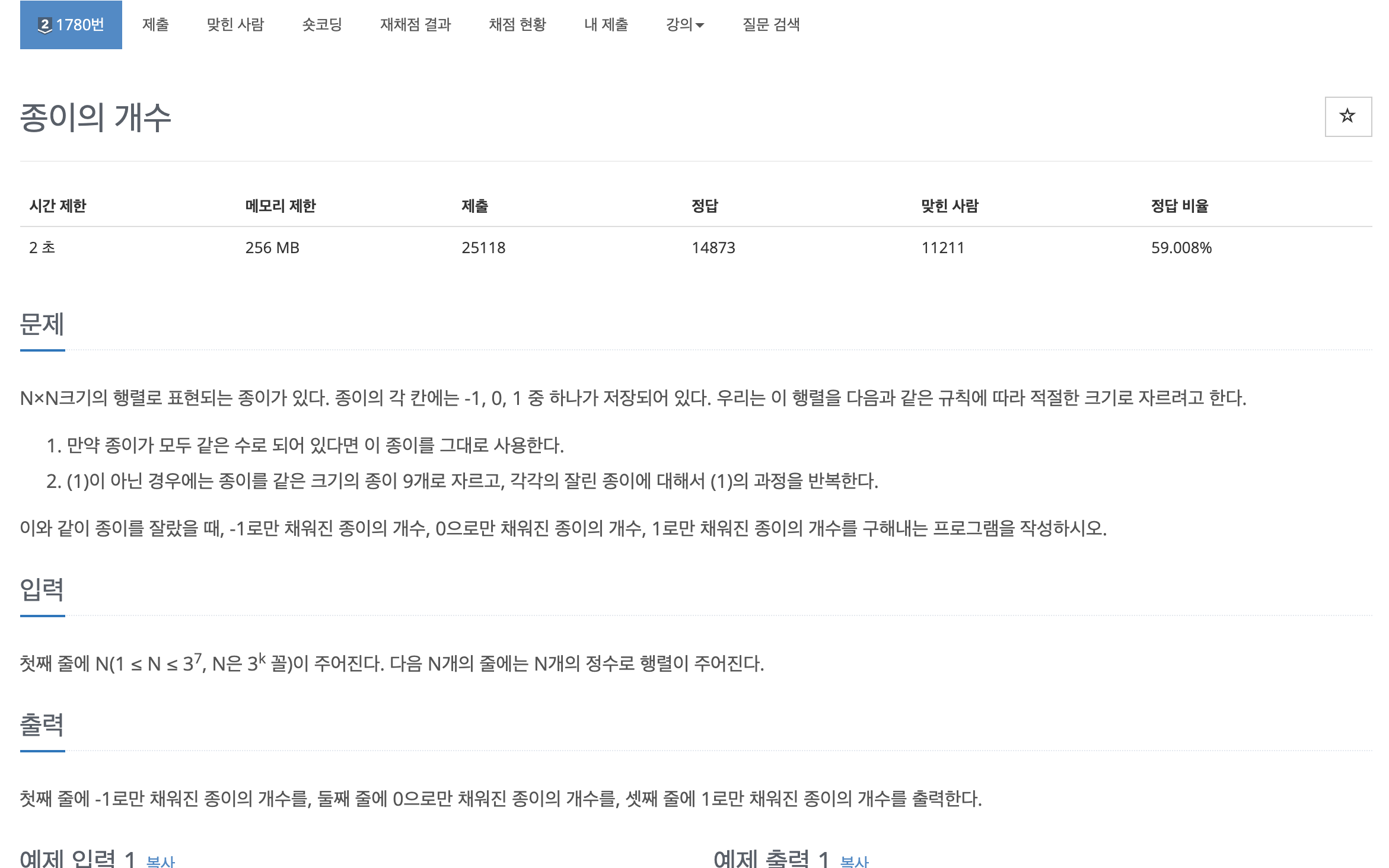
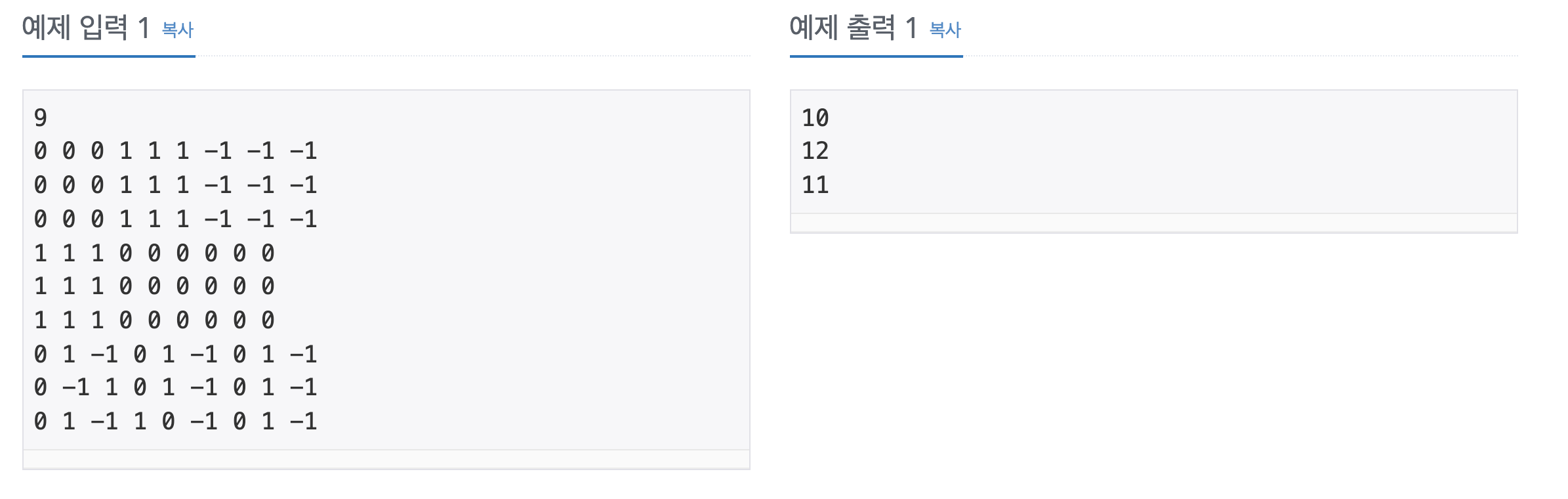
두번째 문제는
- 만약 종이가 모두 같은 수로 되어 있다면 이 종이를 그대로 사용한다.
- (1)이 아닌 경우에는 종이를 같은 크기의 종이 9개로 자르고, 각각의 잘린 종이에 대해서 (1)의 과정을 반복한다.
다음의 두 조건을 만족할때까지 종이를 9분할하고, -1, 0, 1로 채워진 종이의 개수를 출력하는 문제로, 문제를 딱 읽어보면 '분할정복 문제구나'라는 느낌이 온다.
위 문제의 접근 방식은 다음과 같다.
1) 주어진 인풋에 대해 모두 같은 수로 되어 있는지 체크
1-1) 맞다면, 해당 종이의 수에 카운트 +1
1-2) 아니라면, 해당 종이를 9분할 후 다시 1번으로 돌아감.
import sys
n = int(sys.stdin.readline())
paper = [list(map(int, sys.stdin.readline().split())) for _ in range(n)]
neg = 0
neut = 0
pos = 0
#clip_paper의 파라미터로 시작 지점과 몇칸까지 볼지를 함께 받는 것이 포인트!
def clip_paper(x, y, n):
global neg, neut, pos
num_check = paper[x][y]
for i in range(x, x + n):
for j in range(y, y + n):
#같은 수로 이뤄져 있지 않은 경우 분할
if (paper[i][j] != num_check):
for k in range(3):
for l in range(3):
#시작 지점의 경우 k*n//3, l*n//3으로 범위를 조정하며, n값 역시 나누기3!
clip_paper(x + k * n // 3, y + l * n // 3, n // 3)
return
if (num_check == -1):
neg += 1
elif (num_check == 0):
neut += 1
else:
pos += 1
clip_paper(0, 0, n)
print(neg)
print(neut)
print(pos)분할정복, 백트래킹 유형의 재귀를 사용한 유형은 정말 문제 자체를 직관적으로 이해하는 센스 + 어느정도 유형에 대한 풀이방식, 매커니즘을 간단하게는 외우고 있는게 중요한거 같다. 앞으로도 분할정복 문제는 조금 더 신경써서 풀고, 풀고 난 이후에도 기억에 남겨두어야겠다,,
