재귀함수
: 어떤 함수에서 자신을 다시 호출하여 작업을 수행하는 방식의 함수
재귀를 사용하는 대표적인 예시인 팩토리얼 문제
팩토리얼의 2가지 조건
- 0! = 1
- n > 0 이면 n! = n * (n-1)
def factorial(n: int) -> int:
"""양의 정수 n의 팩토리얼을 구하는 과정"""
if n > 0:
return n * factorial(n - 1)
else:
return 1
if __name__ == '__main__':
n = int(input('출력할 팩토리얼 값을 입력하세요.: '))
print(f'{n}의 팩토리얼은 {factorial(n)}입니다.')유클리드 호제법(GCD, 최대 공약수 구하기) 문제
두 정수값의 최대 공약수를 구하는 문제 -> 2개의 정수값을 각각 변의 길이로 갖는 직사각형이 있을때, 이 직사각형 안을 여러 정사각형으로 채워나갈때, 만들수 있는 정사각형 중 가장 작은 작사각형의 변의 길이를 찾는 것과 같은 의미
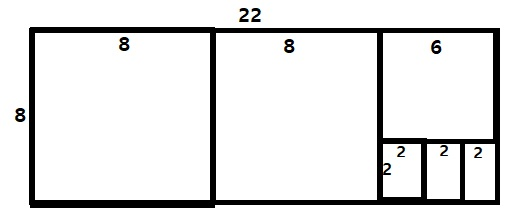
def gcd(x: int, y: int) -> int:
"""정숫값 x와 y의 최대 공약수를 반환"""
if y == 0:
return x
else:
return gcd(y, x % y)
if __name__ == '__main__':
print('두 정숫값의 최대 공약수를 구합니다.')
x = int(input('첫 번째 정숫값을 입력하세요.: '))
y = int(input('두 번째 정숫값을 입력하세요.: '))
print(f'두 정숫값의 최대 공약수는 {gcd(x, y)}입니다.')-> 두 정수값이 주어질때 큰 값을 작은 값으로 나누어 떨어지면 작은 값이 최대 공약수!
재귀 알고리즘 분석
하향식 분석
가장 위쪽에 위치한 상자의 함수 호출부터 시작하여 계단식으로 자세히 조사해 나가는 분석 방법
def recur(n: int) -> int:
"""순수한 재귀 함수 recur의 구현"""
if n > 0:
recur(n - 1)
print(n)
recur(n - 2)
x = int(input('정숫값을 입력하세요.: '))
recur(x)n = 3일때
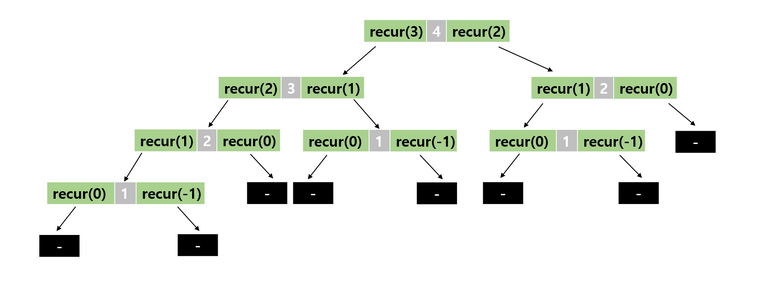
함수 안에서 재귀 호출을 여러번 실행하는 함수
n = 4일때
4 -> recur(3), print(4)#다섯번째 출력, //////////////// recur(2)
-> recur(2), print(3)#세번째 출력, recur(1)#네번째 출력 /////////////// recur(1) print(2) recur(0)
-> recur(1) print(2)#두번째 출력 recur(0)
-> recur(0) print(1)#첫번째 출력 recur(-1)
Output : 1 2 3 1 4 1 2
상향식 분석
하향식 분석과는 반대로 아래쪽부터 쌓아 올리며 분석하는 방식
recur()함수는 n이 양수일때만 실행하므로 먼저 recure(1)이 어떻게 처리되는지를 생각해보면
recur(1) 실행과정
- recur(0) 실행
- 1 출력
- recur(-1) 실행
결국 1만 출력
recur(2) 실행과정
- recur(1) 실행
- 2 출력
- recur(0) 실행
recur(1)과 2출력
이런식으로 recur(4)까지 쌓아올려 도출
비재귀적으로 재귀함수 구현하기(꼬리 재귀를 제거)
꼬리 재귀인 recur(n-2)의 의미는 '인수로 n-2'의 값을 전달하고 recur()함수를 호출
-> 즉, n의 값을 n-2로 업데이트하고 함수의 시작지점으로 돌아감.
def recur(n: int) -> int:
"""꼬리 재귀를 제거한 함수 recur"""
while n > 0:
recur(n - 1)
print(n)
n = n - 2
x = int(input('정수값을 입력하세요.: '))
recur(x)재귀를 제거하기
n 값을 출력하기 전에 recur(n-1)을 실행해야 하기 때문에 n=4인 경우에는 recur(3)의 처리가 완료될 때 까지 4를 어딘가에 저장해야 하며 이를 위해 스택 사용!
from stack import Stack # stack.py의 Stack 클래스를 임포트
def recur(n: int) -> int:
"""재귀를 제거한 함수 recur"""
s = Stack(n)
while True:
if n > 0:
s.push(n) # n 값을 푸시
n = n - 1
continue
if not s.is_empty(): # 스택이 비어 있지 않으면
n = s.pop() # 저장하고 있는 값을 n에 팝
print(n)
n = n - 2
continue
break
x = int(input('정수값을 입력하세요.: '))
recur(x)
분할정복(Divide and Conquer)
문제를 나눌 수 없을때까지 나누어서 각각을 풀면서 다시 합병하여 문제의 답을 얻는 알고리즘
문제 설계 요령
1) Divide : 문제가 분할이 가능한 경우 2개 이상의 문제로 나눔
2) Conquer : 나누어진 문제가 여전히 분할이 가능하면 또 다시 Divide 수행
3) Combine : Conquer한 문제들을 통합하여 원래 문제의 답을 얻음
하노이의 탑 문제
하노이의 탑은 작은 원반이 위에, 큰 원반이 아래에 위치하는 규칙을 지키면서 기둥 3개를 이용해서 원반을 옮기는 문제
원반이 3개일때의 전체 이동 과정
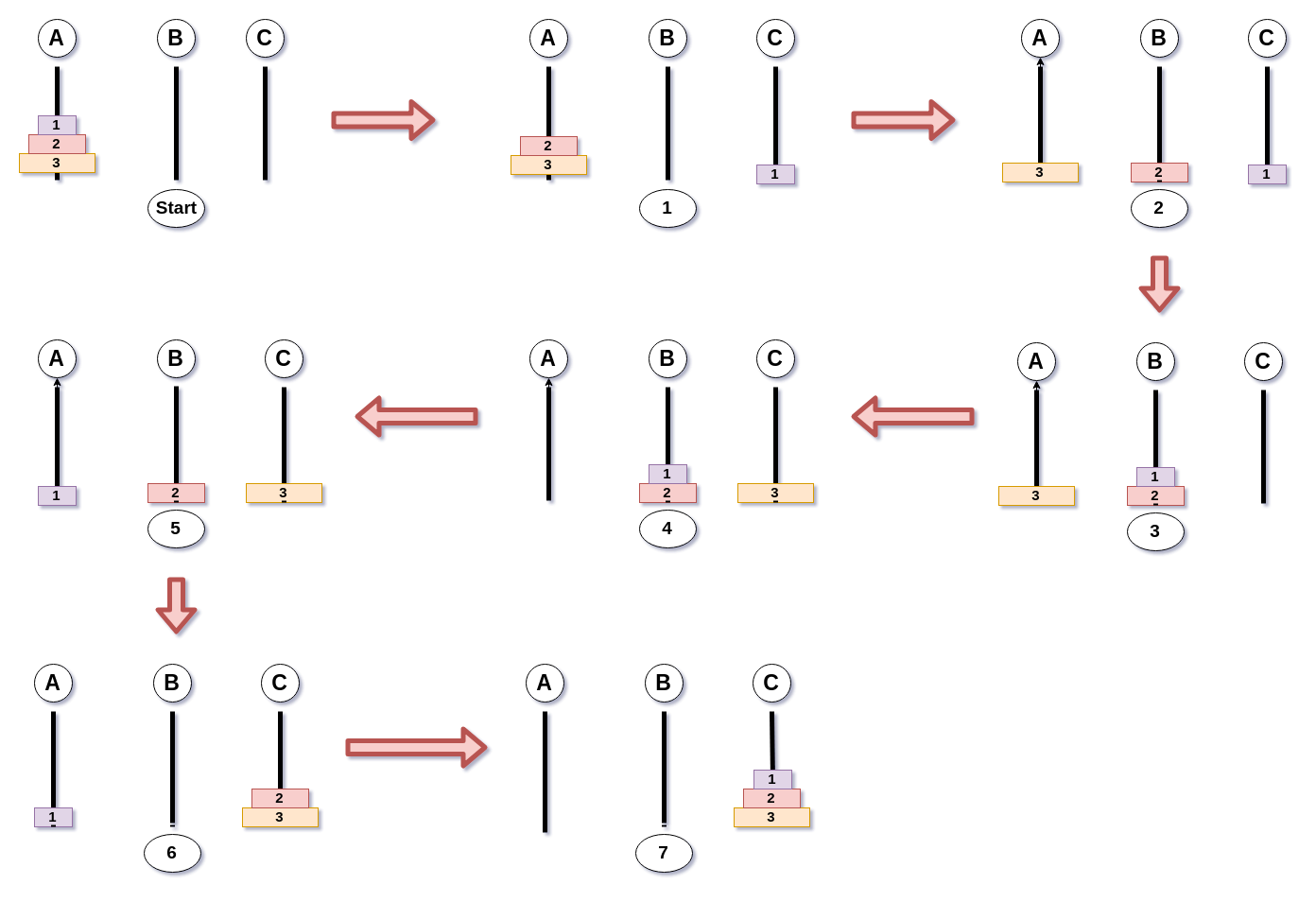
원반이 3개일 때
- 그룹(원반 1,2)을 시작 기둥 -> 중간 기둥
- 원반 3을 시작 기둥 -> 목표 기둥
- 그룹(원반 기둥 1,2)를 중간 기둥 -> 목표 기둥
원반이 2개일 때
- 그룹(원반 1)을 시작 기둥 -> 중간기둥
- 원반 2를 시작 기둥 -> 목표 기둥
- 그룹(원반 1)을 중간 기둥 -> 목표 기둥
원반이 4개일 때
- 그룹(원반 1,2,3)을 시작 기둥 -> 중간기둥
- 원반 4를 시작 기둥 -> 목표 기둥
- 그룹(원반 1,2,3)을 중간 기둥 -> 목표 기둥
def move(no: int, x: int, y: int) -> None:
"""원반을 no개를 x 기둥에서 y 기둥으로 옮김"""
if no > 1:
move(no - 1, x, 6 - x - y)
print(f'원반 [{no}]을(를) {x}기둥에서 {y}기둥으로 옮깁니다.')
if no > 1:
move(no - 1, 6 - x - y, y)
print('하노이의 탑을 구현하는 프로그램입니다.')
n = int(input('원반의 개수를 입력하세요.: '))
move(n, 1, 3)8퀸 문제

8 퀸 문제는 8x8크기의 체스판에 퀸을 8개 배치하는 문제이다. 1848년 막스 베첼이 처음 제안하였다. 이 문제를 일반화하면 NxN 크기의 체스판에 퀸을 N개 배치하는 N 퀸 문제
pos = [0] * 8 # 각 열에 배치한 퀸의 위치
flag_a = [False] * 8 # 각 행에 퀸을 배치했는지 체크
flag_b = [False] * 15 # 대각선 방향(↙↗)으로 퀸을 배치했는지 체크
flag_c = [False] * 15 # 대각선 방향( ↘↖)으로 퀸을 배치했는지 체크
def put() -> None:
"""각 열에 배치한 퀸의 위치를 출력"""
for i in range(8):
print(f'{pos[i]:2}', end='')
print()
def set(i: int) -> None:
"""i 열의 알맞은 위치에 퀸을 배치"""
for j in range(8):
if( not flag_a[j] # j행에 퀸이 배치 되지 않았다면
and not flag_b[i + j] # 대각선 방향(↙↗)으로 퀸이 배치 되지 않았다면
and not flag_c[i - j + 7]): # 대각선 방향( ↘↖)으로 퀸이 배치 되지 않았다면
pos[i] = j # 퀸을 j행에 배치
if i == 7: # 모든 열에 퀸을 배치하는 것을 완료
put()
else:
flag_a[j] = flag_b[i + j] = flag_c[i - j + 7] = True
set(i + 1) # 다음 열에 퀸을 배치
flag_a[j] = flag_b[i + j] = flag_c[i - j + 7] = False
set(0) # 0열에 퀸을 배치