Chapter 9. Relations
9.0 Chapter Summary
- Relations and Their Properties
- Representing Relations
- Closures of Relations
- Equivalence Relations
- Partial Orderings
9.1 Relations and Their Properties
section summary
(1) Relations and Functions
(2) Properties of Relations
• Reflexive Relations
• Symmetric and Antisymmetric Relations
• Transitive Relations
(3) Combining Relations
binaty relations (이진 관계)
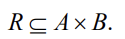
R의 순서쌍 : (a,b)
a는 A의 원소, b는 B의 원소
표기법(Notation)
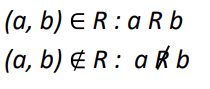
reflexive relations(반사 관계)
집합 A에 속한 원소 a에 대해 집합 R에 (a,a)의 순서쌍이 속한 관계
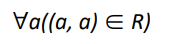
symmetric relations(대칭 관계)
순서쌍 (a,b)가 R에 속해있다면, (b,a)도 R에 속해있어야 한다는 관계
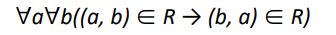
Antisymmetric relations
(a,b)가 R에 속해 있고, (b,a) 도 R에 속해있다면, a = b 라는 관계
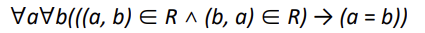
Transitive relations(전이적 관계)
(a,b)가 R에 속해 있고, (b,c)도 R에 속해 있다면, (a,c)도 R에 속한 관계
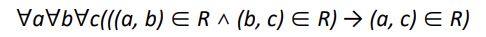
Combining relations (결합 관계)
2개의 관계 R1, R2가 있을 때, 그 두 관계간의 결합 관계
합집합, 교집합, 차집합 등등
composition
(x,y) -> R , (y,z) -> S 일 때,
(x,z) -> S o R
f o g(x) 합성 함수의 개념이라고 생각하면 편함.
powers of a relation
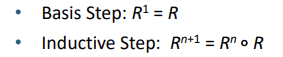
9.3 Representing Relations
section summary
(1) Representing Relations using Matrices
(2) Representing Relations using Digraphs
Representing Relations Using Matrices
A X B의 부분집합 R에 대해서 (a,b)가 R에 속해있으면, 행렬에서 1로 표현,
(a,b)가 R에 속해있지 않으면, 0으로 표현한다.
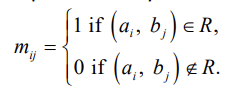
Matrices of Relations on Sets
-
Reflexive relation
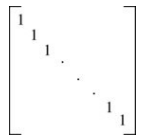
행렬 M에 대해 주대각선(main diagonal)의 원소가 모두 1인 경우 Reflexive relation 을 만족
-
symmetric relation
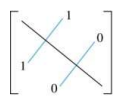
주대각선을 기준으로 대칭인 경우 symmetric
- antisymmetric relation
주대각선을 기준으로 대칭시켰을 때, 원소의 값이 1인 경우에는 대칭된 원소가 0을,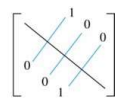
원소가 0인 경우에는 대칭된 원소가 0을 가리킬 경우 antisymmetric
Representing Relations Using Digraphs
원소쌍들의 관계를 그래프로 표현한 것.
ex)
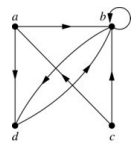
1) reflexivity
-> 그래프에서 모든 원소의 점들이 loop적인 관계
2) symmetry
-> (x,y)의 대응관계가 있으면, (y,x)도 있어야 함.
3) antisymmetry
-> (x,y) 관계에서 x와y가 다르다면, (y,x)가 있으면 안됨.
4) transitivity
-> (x,y) , (y,z)가 있다면, (x,z)도 존재
9.4 Closures of Relations
section summary
(1) Closures
(2) Paths in Directed Graphs
(3) Transitive Closures
(4) Warshall’s Algorithm
closures
집합 A에 대한 관계 R이 있을 떄, R은 reflexivity, symmetry, or transitivity 같은 관계적 특성을 가질 수도 안가질 수도 있다. 이런 관계적 특성을 P라고 할 때,
R을 포함한 특성 P의 모든 관계의 부분집합을 S라고 할 때, 우리는 이를 closure 라고 부른다.
(1) Reflexive closure
예를 들어, 관계 R = {(1, 1), (1, 2), (2, 1), (3, 2)} 이라면, 이 관계 R이 reflexive한 관계를 만족하려면, (2,2) , (3,3)이 추가되어야 한다.
우리는 이렇게 relexive를 만족시킬 수 있도록 최소한의 원소를 추가시켜 만들어진 집합을 closure 라고 부른다.
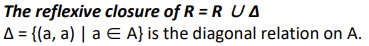
(2) symmetric closure
관계 R이 symmetric 관계의 조건을 만족하기 위해 최소한의 원소가 추가된 집합 S

(3) transitive closure
관계 R이 transitive를 만족하기 위한 최소한의 원소가 추가된 집합으로
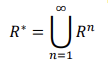
R^ = R^1 V R^2 V ... R^n 으로 일정 이상의 n부터는 더 추가가 되어도 동일한 집합이 유지된다.
R^2 -> R^1에서의 R^1에 있는 원소에서만 transitvie를 만족하는 원소 추가,
R^3 -> 위에서 얻어진 R^2에 있는 원소만으로 추가
이 과정의 반복을 통해 R^ 를 찾는다.
Paths in directed graphs
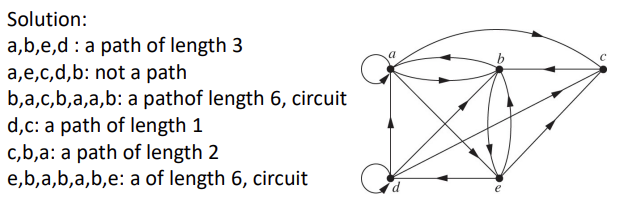
위의 그래프를 보고 이해하는 것이 쉽다.
Warshall’s Algorithm
transitive closure 를 계산하기 위한 효율적인 방법
ZERO-ONE matrices의 구조를 통해 W0, W1, W2 ... Wn을 찾아가는 과정
W0: a,b,c,d의 관계 R에 대해서 초기 matrix
W1: 1행과 1열에 대한 원소 조합 추가
W2: W1에서 2행과 2열에 대한 원소 조합 추가
Wn: Wn-1에서 가장 마지막 행과 열에 대한 원소 조합 추가
Equivalence Relations
section summary
(1) Equivalence Relations
(2) Equivalence Classes
(3) Equivalence Classes and Partitions
equivalence relations(동치관계)
집합 A의 관계가 reflexive, symmetric, transitive를 만족한다면, 이를 equivalence relations 이라고 한다.
표기법(notation)
2개의 원소 a,b가 그 동치관계를 만족
a~b
equivalence classes(동치류)
집합 A의 원소 a에 관계된 모든 원소들의 집합을 의미
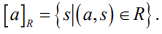
예를 들어, 원소 a에 대해 a-4n의 관계가 존재하는 원소들의 동치류는
[0]_4 = {...,-8,-4,0,4,8...}
[1]_4 = {...,-7,-3,1,5,9...}
로 표현할 수 있을 것이다.
Equivalence Classes and Partitions
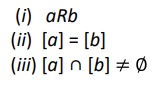
집합 A에 대한 동치관계의 집합 R에 대해서 포함된 원소 a,b가 동치적인지 확인하는 방법
Partition of a Set
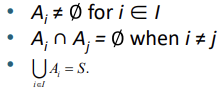
집합 S의 부분집합 독립사건에 대한 집합이라고 생각하면 편함
An Equivalence Relation Partitions a Set
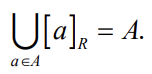
집합 A에 속하는 원소에 대해서 a와 b가 있을 떄,
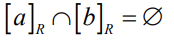
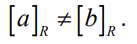
예를 들어, 집합 S = {1,2,3,4,5,6}을 포함하고 있을 때, A1 = {1,2,3},
A2 = {4,5}, A3 = {6} 은 서로 교집합이 없으며, 각 부분집합들의 합은 집합 S를 만족한다.
