야, 너두 재귀할 수 있어: 재귀가 풀리는 4단계 접근법

Eddy·2021년 12월 19일

algorithm data structure

재귀의 벽

솔직히 처음 알고리즘 공부를 할 땐, 꽤나 의기양양했다.

어, 풀리네? 재밌네? 하면서 문제를 풀었다.
'뭐지, 나 좀 잘하는 건가?' 으쓱해졌다.

(이렇게 무식한 사람이 자신의 실력을 과대평가하는 것을 '더닝-크루거 효과'라고 부른다...)

하지만 거기서 조금 더 나아가자 갑자기 멘탈을 와장창 부수는 놈이 등장했다.
바로 '재귀의 벽'에 도달한 것이다.

(출처: 진격의 거인)

너무 어려웠다. 심지어 이제는 답을 봐도 이해가 가지 않았다.

함수 실행 순서를 하나씩 설명하는 친절한 풀이를 찾아봤다. 그걸 하나하나 훑다보니, 그제서야 이렇게 되는 거구나 싶다.

하지만 처음보는 문제를 다시 푼다면? 여전히 내가 이걸 생각해낼 수 있을 것 같지가 않다.

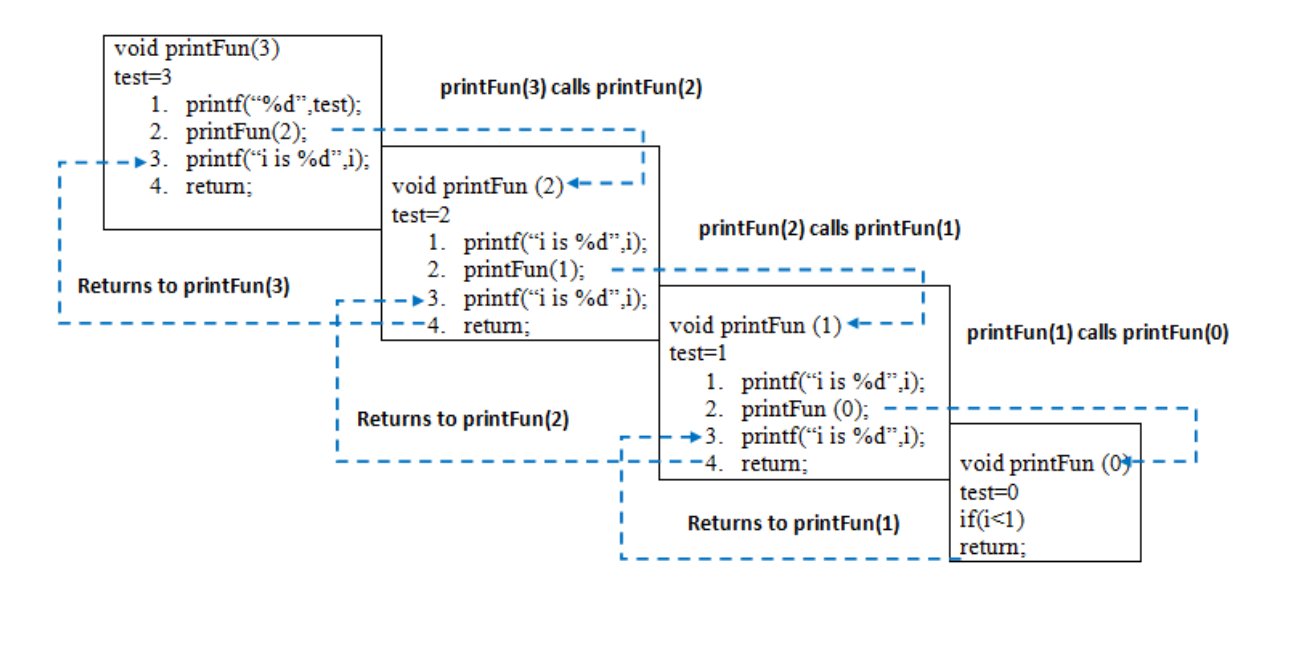
(출처: geeksforgeeks)

특히 함수의 실행 순서를 따라서 인풋, 아웃풋의 변화를 머릿속에 그리는 게 너무 어려왔다.

자기가 자기 자신을 호출하고, 그러면서 인자값은 n이 되고...
그걸 다시 호출하고, 그걸 또 다시 호출하고...

머리가 아프다.
무한히 뻗어가는 거울 반사를 보면서 느끼는 어지러움이랄까.

그래서 한동안 재귀를 써야하는 걸 알면서도 반복문을 썼다. 불안했다. return에 무슨 값을 써야 하지? 무한 반복될 거 같은데?

조금 더 나가자, 이번에는 더 높은 벽이 가로막았다.
재귀를 2번씩 호출하는 알고리즘 (DFS)가 등장한 것이다.

음... 왼쪽 노드를 넣어서 호출했다가,
또 그 함수에서 왼쪽 노드와 오른쪽 노드를 호출하고....

여기서부터는 정말 머릿속에 스택 오버플로우가 와버렸다.

재귀적으로 생각하지 말자

하지만 포기하지는 말자. 왜냐, 재귀 문제를 쉽게 푸는 방법은 분명 있기 때문이다.

처음엔 나도 어려웠지만, 무식하게 재귀 문제를 풀다보니 재귀 문제를 푸는 노하우가 생겼다.
이미 훌륭한 개발자들이 자신들의 노하우를 여러가지 방식으로 정리해놓은 걸 보니, 거의 비슷한 접근법을 쓰고 있었다.

이 접근법이 익숙해지고 나니, 이제는 재귀가 하나도 무섭지 않아졌다.

그 비결이 무엇이냐고? 그건 바로...

재귀적으로 생각하지 말 것.

읭? 이게 무슨 소리인가. 재귀 문제를 푸는데 재귀적으로 생각하지 말라고?

정확히 말하면, 머릿속에 함수 실행 순서를 그리려고 하지 말라는 말이다.

재귀 문제가 익숙해지고 쉬워진다는 건, 갑자기 내 머릿속에 함수 콜 스택이 어떻게 쌓이는지 쫙 그려지는 게 아니다. (물론 그런 대단한 사람이 있을 거다..)

대부분의 사람은 아무리 재귀를 풀어도 재귀의 재귀의 재귀...를 머릿속에 떠올리기 어렵다.

내 경우에는 오히려 그렇게 생각하지 않는 게 도움이 됐다. 머릿속에서 재귀 함수의 실행 순서를 그려보려고 하면 거기서부터 압도당해버린다.

즉, 처음부터 큰 그림을 머릿속에 그리려고 하지 않는다. 재귀 함수의 중요한 부분들에만 초점을 좁혀서 문제를 풀어나간다.

이렇게 하면 정말 재귀적으로 생각하지 않고도 재귀 문제를 풀 수 있다!

야, 너두 재귀할 수 있어!

재귀가 풀리는 4단계 접근법

1단계. 재귀를 꼭 써야 하는가?
2단계. 베이스 조건: 답을 바로 알 수 있는 가장 간단한 상황을 생각한다.
3단계. 분해: 베이스 조건에 가까워지도록 인풋값을 조작한다.
4단계. 조합: 부분 답을 가지고 전체 답을 구하는 방법을 생각해본다.

1단계. 재귀를 꼭 써야 하는가?

반복 대신 재귀를 써야하는 경우인지 생각해본다.

재귀로 풀 수 있는 문제는 반복으로도 풀 수 있다.

복잡한 문제를 더 작은 문제로 쪼갠다.
작은 문제를 푸는 작업을 반복한다.
작은 문제의 답을 조합해서 전체 문제를 해결한다.

이게 재귀 알고리즘이다.

그런데 이건 반복문을 쓰는 알고리즘도 마찬가지다.
for나 while 문을 사용하면 어떤 작업을 반복해서 전체 문제를 풀 수 있다.

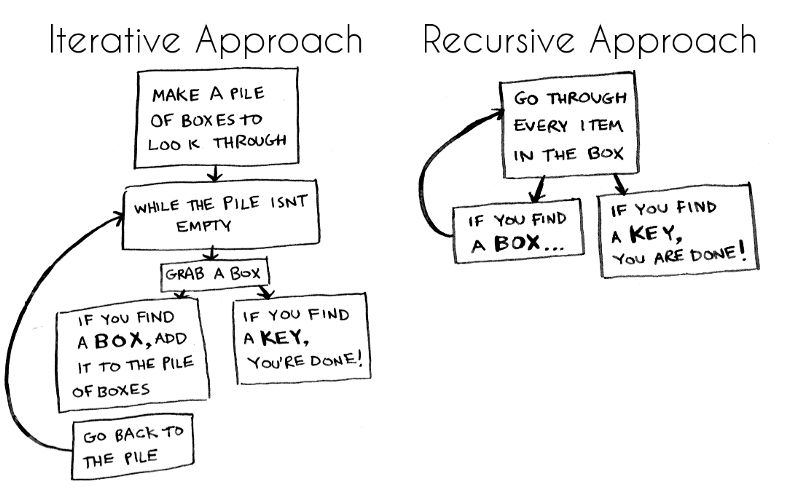
(출처: freecodecamp)

일반적으로 성능은 반복문이 더 좋다.

반복문은 계속해서 코드의 앞으로 돌아가서 다시 실행한다.

반면 재귀문은 함수를 새로 호출하고 스택에 쌓은 뒤 실행한다. 재귀를 사용하면 스택에 함수와 관련된 정보가 쌓인다. 매개변수, 반환되었을 때 돌아갈 위치 등. 그냥 반복문을 선언한 지점으로 점프해버리는 반복문보다 좀 더 복잡하다. 함수가 끝나지 않은 상황에서 계속 함수가 호출되기 때문에 스택의 깊이는 계속 깊어진다. 메모리를 많이 차지한다.

'꼬리 재귀 최적화'라는 게 있다. 재귀의 성능 문제를 해결하기 위한 방법이다. 컴파일러가 재귀 알고리즘을 해석해서 반복문으로 바꿔 실행한다.

꼬리 재귀 최적화는 1) 반환값이 재귀 호출 결과값일 때, 2) 컴파일러가 꼬리 재귀 최적화를 지원할 때 가능하다.

사실 꼬리 재귀 최적화를 쓸 수 없고 실행 횟수가 엄청 많은 일부 케이스를 제외하면, 재귀가 성능에 큰 문제가 될 건 없다고 한다. 하지만 어쨌든 반복문은 그런 문제가 없으니, 성능에선 반복문이 낫다고 할 수 있다.

그럼 왜 재귀를 쓸까?

재귀를 써야하는 경우는, 간단하게 2가지만 기억하자.

1. 재귀적인 자료구조나 풀이 공식이 있을 때

재귀적인 자료구조

어떤 자료 구조 안에 동일한 자료 구조가 중첩되어있는 형태를 떠올리면 된다.

링크드 리스트(linked list)가 대표적이다. 링크드 리스트 안에 있는 포인터가 다음 링크드 리스트를 가리키고, 그 링크드 리스트의 포인터가 또 다음 링크드 리스트를 가리킨다.

링크드 리스트, 트리, 그리드, 중첩 배열, JSON, HTML 등이 재귀적인 자료 구조다. 우리가 프로그래밍을 할 때 자주 다루는 자료구조들이다.

이런 자료 구조를 다룰 때는 재귀 알고리즘이 아주 유용하다. 보통 우리가 재귀를 처음 맞닥 뜨리는 경우도 링크드 리스트나 트리 같은 자료 구조를 공부할 때다.

재귀적인 풀이 공식

답을 구하는 공식이 재귀적인 경우도 있다. 팩토리얼, 피보나치 수열, 순열/조합 등이 바로 여기 속한다.

예를 들어 피보나치 수열은 f(n) = f(n-1) + f(n-2)라는 식으로 구할 수 있다. 이 공식 자체가 재귀적이다. 이럴 때는 재귀를 사용한 알고리즘으로 풀었을 때 깔끔하게 그 공식을 보여줄 수 있다.

이렇게 재귀적인 자료구조나 풀이 공식이 있는 문제는 재귀로 적으면 코드가 깔끔해지고, 방법이 더 명료하게 드러난다. 쉽게 말해, 링크드 리스트, 트리 같은 재귀적인 자료 구조가 나왔을 때나, 규칙성을 찾아보니 재귀적인 형태라면 재귀를 써도 되겠군! 이라고 생각하자.

2. 변수 선언 없이 코딩하고 싶을 때

함수형 프로그래밍에서는 변수 선언을 금지한다. 값은 변하지 않는 상수로 선언한다. 유식한 말로 불변성(immutability)라고 한다.

이 경우에는 재귀가 유용하다. 재귀는 함수를 호출할 때마다 새로운 스코프를 생성하기 때문에, 변수 없이도 문제를 풀 수 있다.

문제를 보면 먼저 이 2가지 조건에 해당하는지 확인하자. (알고리즘 문제에서 2번 제약이 있는 경우는 잘 없기 때문에 아마 대부분은 1번에 해당할 것이다.) 해당한다면 재귀 함수를 '굳이' 써야하는 상황이다.

자, 이제 본격적으로 재귀 함수를 설계 해보자.

2단계. 베이스 조건

답을 바로 알 수 있는 가장 간단한 상황을 생각한다.

무조건 베이스 조건부터

재귀 함수를 풀 때, 가장 먼저 '베이스 조건'을 떠올려야 한다.

문제에 무슨 예시가 나와있든 상관없다.
요구하는 조건이 얼마나 복잡한지도 상관없다.

일단은 머릿속에서 치우자.
'베이스 조건'부터 생각해보자. 이게 아주 중요하다.

'베이스 조건'이란 더 이상 자기 자신을 호출하지 않게 하는 조건이다.
다시 말해, 재귀가 끝나는 조건이다.

베이스 조건은 재귀 함수에 반드시 있어야 한다. 베이스가 없으면 재귀 함수는 무한히 자기 자신을 호출하게 될 테니까.

베이스 조건이 재귀를 멈추는 조건이라고 하니 이렇게 생각하기 쉽다. '음... 어디까지 호출이 되고, 값이 어떤 상태가 되었을 때 재귀를 멈춰야하지? 하지만 이렇게 시작하면 안 된다!

그렇게 생각하면 머릿속으로 함수 실행 순서를 그려야 한다. 하지만 우리의 목표는 '최대한 재귀적으로 생각하지 않는 것'이다.

대신 이렇게 생각해본다.
베이스 조건은 단순한 작업으로, 바로 답을 구할 수 있는, 가장 쉬운 상황이다.

바로 답을 구할 수 있는, 가장 단순한 인풋값은 무엇일까?

마치 거저먹는 것처럼 느껴지는 그런 인풋값을 떠올려보자.

0과 1을 활용한 인풋

이 때 가장 간단한 인풋값은 0 혹은 1인 경우가 많다.

만약 정수 타입이 들어온다면,
인풋이 0이나 1인 상황을 생각해보자.

만약 배열이 들어온다면?
그러면 배열의 길이가 0인 경우(빈 배열), 배열의 길이가 1인 경우를 생각해보자.

만약 트리가 들어온다면?
인풋값이 nil인 경우, 혹은 자식 노드가 nil(잎 노드)인 경우를 생각해보자.

만약 인풋값이 2차원이라면?
인풋값이 m x n 그리드 (이차원 배열)이라면,
둘 다 0이거나 (m = 0, n = 0),
둘 중 하나가 1이거나 (m = 0, n = 1) (m = 1, n = 0)
둘 다 1인 (m=1, n=1) 케이스를 생각해보자.

0과 1을 사용한 인풋값이 들어왔을 때 즉각 답을 구할 수 있는가?
만약 YES라면, 그게 베이스 조건과, 베이스 조건에서의 결과값이 된다.

물론 0과 1이 항상 적절한 베이스 조건인 건 아니다. 추가적인 베이스 조건이 필요할 때도 있고, 둘 중 하나만 필요할 수도 있다. 하지만 대개 0과 1을 떠올리면 쉽게 베이스 조건을 찾을 수 있다.

문제에서 요구한 답의 데이터 타입

베이스 조건에서 무엇을 return 해야할지 헷갈린다면 문제에서 요구한 답의 데이터 타입을 보자.

예를 들어, 트리가 주어지고, 트리 안 어떤 경로의 '노드값 총합(정수)'를 구하는 문제다. 그러면 베이스 조건의 결과값은 '정수 타입'이다.

비슷지만 조금 다른 문제. 트리가 주어지고, 특정한 경로의 '트리 노드 자체'를 구하는 문제다. 그러면 베이스 조건의 결과값은 '트리 노드 타입'이다.

이런 식이다. 베이스 조건만 주어져도 재귀 함수는 답을 뱉어야 한다.

문제가 요구하는 데이터 타입과 베이스 조건 결과값의 데이터 타입은 같아야 한다. 너무도 당연한 말이지만, 헷갈릴 땐 은근히 좋은 힌트가 된다.

다시 한번 강조하지만, 무조건 '베이스 조건'부터 생각해야 한다. 재귀로 풀어야겠다고 마음을 먹은 순간, 자동적으로 머릿속에 '베이스'가 떠올라야 한다.

베이스 조건은 문제를 쉽게 풀도록 도와주는 출발점이다.

예시로 주어진 인풋값을 보고, 어떻게 이걸 답으로 만들지? 라고 생각하면 안 된다. 자꾸 함수 실행 순서를 생각하게 되기 때문이다.

최대한 재귀적으로 생각하지 않고, 마치 1차원 문제인 것처럼 푸는 게 우리 전략이다.

3단계. 분해

베이스 조건에 가까워지도록 인풋값을 조작한다.

재귀적 분해 = 문제를 더 작게 만드는 것

베이스 조건을 정했다. 하지만 끝이 아니다. 재귀 함수가 잘 작동하려면, 함수를 호출할 때마다 베이스 조건에 가까워져야 한다.

자기 자신을 호출할 때, 넣을 인자를 한 단계 더 간단해지도록 조작한다.

예를 들어 n이라는 정수를 인자로 받았다면, 자기 자신을 호출할 때 n-1을 넣는 식이다. 그래야 재귀를 반복하면서 인풋값이 조금씩 더 간단해진다.

그러다 어느 순간 인풋값이 베이스 조건에 턱! 하고 걸린다. 재귀 호출이 멈춘다. 이제 값을 반환한다. 이게 재귀 함수의 기본 원리다.

이걸 영어로는 재귀적 분해(Recursive Decomposition)이라고 한다.

어려운 말처럼 들리지만, 인풋값을 간단하게 만들어서 문제를 더 작게 만드는 것. 이라고 생각하면 쉽다. 이 글에서는 편의상 ‘분해'라고 부르도록 하겠다.

자, 우리가 보고 있는 문제의 인풋값은 무엇인가? 이 값에 어떤 조작을 가해줘야 베이스 조건으로 향하게 될까?

분해의 흔한 패턴

‘분해’도 재귀 문제를 많이 풀다보면 비슷한 패턴이 반복된다.

정수 타입이라면 대체로 n - 1 혹은 n - 2.
배열이라면 앞의 숫자 하나를 떼고 길이를 줄인다. [1,2,3,4] → [2,3,4] → [3,4] 이런 식으로. 문자열도 마찬가지.
링크드 리스트라면, 포인터가 가리키는 다음 노드, 혹은 다다음 노드를 넣는다.
트리라면, 자식 노드를 하나씩 넣는다. (이진 트리의 경우 재귀 호출을 2번 하는 경우가 많다.)

‘분해'라고 해서 꼭 값을 줄이는 건 아니다.

하지만 계속 분해하다보면 우리가 원하는 베이스 조건에 도달해야 한다. 그게 중요하다.

분해를 어떻게 해야할지 바로 떠오르지 않아도 괜찮다. 문제에 따라서 분해가 상당히 복잡할 수 있다.

일단은 단순하게 가정하고 넘어가자. 어떤 분해가 적절한지 다음 ‘조합' 단계에서 힌트를 얻는 경우가 많다.

4단계. 조합

부분 답을 가지고 전체 답을 구하는 방법을 생각해본다.

조합은 재귀 호출이 베이스 조건에 걸려 멈추고 나서, 그 다음에 일어나는 작업이다.

베이스 조건에 도달하고, 거기서부터 마치 감았던 실타래를 풀듯이 결과값들이 차례차례 반환된다.

마치 테트리스에서 한 줄이 터지면 다음 블록이 내려오면서 연속적으로 터지는 그런 느낌이다. 재귀의 꽃이랄까.

하지만 그 과정을 다 머릿속에 그릴 필요는 없다.
우리는 최대한 재귀적으로 생각하지 않는 게 목표다.

어떻게 하면 조합을 쉽게 생각할 수 있을까?

조합은 부분 답을 조합해서 전체 답을 만드는 과정이다.
재귀 과정 전체의 조합을 생각하지 말고, 특정한 단계를 딱 집어서 본다.

그 단계에서 바로 밑의 재귀 호출로 얻은 답을 가지고, 현재 단계의 답을 어떻게 낼 것인가? 를 생각하면 된다.

조합을 어떻게 할까? 이 문제는 대개 두 가지 케이스를 생각해보면 풀린다.

1) 베이스 조건 바로 위의 단계

베이스 조건에 도달하고 나서, 재귀 함수가 결과값을 반환한다.

그 바로 윗 단계의 함수를 생각해본다. 분해를 하기 직전 함수가 실행되었을 때를 말한다.

n == 1 이 베이스 조건이다.
분해는 func(n-1)이었다.

그러면 베이스 조건 바로 윗단계의 함수는?
n이 2일 때다.

array.length == 1이 베이스 조건이다.
분해는 func(array.remove(at: 1)) 이었다.

그러면 베이스 조건 바로 윗단계의 함수는?
array 길이가 2일 때다.

예를 들어, n부터 1까지의 합을 구하는 함수를 짠다고 해보자.

n이 2일 때 어떤 답이 나와야 할까 생각해본다.

그냥 손으로 풀어보자. 베이스 바로 위의 인자값도 단순하다. 손으로 풀어도 답을 알 수 있다. f(2)는 당연히 3이다.

그 다음 베이스 조건에서 반환되는 값을 가지고, 이 답을 어떻게 만들지 생각해본다.

f(1)은 1이었다. 이걸로 어떻게 3을 만들까? 2를 더해주면 되지 않을까? 그러면 될 거 같다.

2) 베이스 조건의 3단계 위

이번에는 베이스 조건에서 3단계 위를 생각해본다.

사실 꼭 3단계일 필요는 없다. 아무거나 가정해도 좋다. 보통 베이스에서 3단계 위 지점까지는 직접 풀어도 쉽게 답이 나오고, 3단계 위 지점에서 제대로 작동한다면 대부분 잘 작동할 것이다. 그래서 3단계 위를 많이 가정하는 편이다.

앞에서 했던 것처럼 분해를 3번 뒤로 돌리면 된다.
n == 1이 베이스 조건이었으니, n이 4일 때 3단계 위가 된다.

n이 4일 때 답을 생각해본다. 4+3+2+1 = 10이다.

그리고 n이 3일 때 답을 생각해본다. 3+2+1 = 6이다.

일단 믿어본다

여기서 중요한 개념이 나온다. 바로 아랫단계의 재귀 호출에서 정답을 반환해준다고 가정하는 것이다.

우리는 아직 재귀 함수가 잘 설계되었는지 모른다. 하지만 일단은 f(3)을 호출하면 그냥 정답인 ‘6’을 구해준다고 믿어본다. 일단 어떤 방식으로 구현했는지 몰라도 ‘맞다 치고’ 해보는 거다.

그러면 조합을 생각하기가 쉬워진다.

왜냐하면 밑으로 내려가는 재귀 함수의 실행을 머릿속에 그릴 필요가 없기 때문이다. 그냥 아랫단계의 답이 나왔고, 그걸 어떻게 지금 단계의 답으로 만들 수 있을지만 생각해본다.

이걸 ‘재귀적 믿음의 점프 (Recursive leap of faith)’라고 부른다. 영어식 표현이라 어색하다면 그냥 ‘일단 믿어본다’로 기억하자.

이 믿음은 조합을 생각할 때 큰 도움이 된다.

왜냐하면 비록 베이스 조건에서 3단계만 위라고 하더라도, 재귀 호출이 2번 등장하는 트리나, 4번 등장하는 그리드 탐색 같은 경우엔 아랫단계의 실행 순서가 복잡하고 골치 아프기 때문이다. 하지만 구현은 됐고 일단 아래 단계에서 답이 나왔다고 가정하면, 조합을 구현하는 게 훨씬 쉬워진다.

두 케이스의 공통점을 찾는다

‘베이스 바로 위’ ‘베이스 3단계 위' 이 두가지 조합을 똑같은 방식으로 일치하게 할 수 있을까? 둘 다 정확한 답이 나올 수 있는 방식을 찾았다면, 재귀 설계는 끝났다.

이 2단계에서 제대로 답이 나온다면, 거의 모든 경우에 재귀는 자연스럽게 답으로 가게 되어있다. 마치 점 2개를 찍고 그 사이를 이으면 직선이 나오는 것처럼 말이다.

자 여기까지 끝났다면, 이제 베이스 조건, 분해, 조합의 순으로 코드를 작성하면 된다.

이 4단계는 그야말로 ‘접근법'이다. 대입하면 바로 풀리는 공식은 아니다.

하지만 알고리즘 문제를 재귀로 풀 때 가장 중요한 점은, 코드를 치기 전에 이런 접근법을 가지고 문제를 어떻게 풀지 생각해보는 것이다.

코드를 치기 전에 먼저 문제를 풀어야 한다. 머릿속으로 그려보다가 조금 복잡하다 싶으면, ‘일단 코드부터 작성하다보면 어떻게 되겠지 라는 마음으로 시작하기 쉽다. 그러면 막혔을 때 오랫동안 헤멘다. 내가 손으로 풀 수 없는 문제를 컴퓨터에게 시킬 수는 없다.

4단계를 차례로 생각해보면 코드를 치기 전에, 먼저 알고리즘을 설계할 수 있다. 코드를 쓰는 일이 훨씬 쉬워진다.

예제 풀어보기

문제를 풀어보면서 4단계 접근법을 적용해보자.

1. 문자열 뒤집기 (Reverse String)

문제

문자열 s가 주어진다. 이 s를 뒤집어서 반환하는 함수를 만들어라.
ex) reverseString(“hello”) → “olleh”

(출처: leetcode)

1단계. 재귀를 꼭 써야하는가?

반복이 아니라 굳이 재귀로 풀어야 하는 문제일까? 사실 답은 ‘No’다.

이 문제는 반복문으로도 쉽게 풀 수 있다. 딱히 재귀로 풀어야할 이유는 없어보인다.

하지만 여기선 가장 간단한 예제를 먼저 보여주려고 일부러 가져왔다. 일단 넘어가도록 하자.

2단계. 베이스 조건

답을 바로 알 수 있는 가장 간단한 상황은 무엇일까?
예시에는 인풋으로 ‘hello’가 주어져있다. 하지만 일단 머릿속에서 치워둔다.

가능한 문자열 중 가장 간단한 건 뭘까? 일단 0과 1을 사용해서 가장 간단한 인풋을 생각해본다.

먼저 떠오르는 건, string의 길이가 0과 1인 경우다.

만약 string의 길이가 0이라면, 문제는 간단하게 풀린다. 그냥 빈 배열을 return 하면 된다.
만약 string의 길이가 1이라면, 역시 문제가 간단하게 풀린다. 주어진 인풋을 그대로 return 하면 된다.

string 길이 == 0  → return ""
string 길이 == 1  → return str

3단계. 분해

재귀 호출을 거듭하면서 베이스 케이스에 가까워지도록 인풋값을 조작한다.

만약 “hello”라는 문자열이 주어진다면, 어떻게 분해해야할까?

가장 간단한 건, 앞의 한 글자를 빼는 거다. 앞의 한 글자를 빼고 재귀 호출의 인자로 넣어주자.

그러면 인풋값은 "hello" → "ello" → "llo" → "lo" → "o" 로 분해된다. 어떤 문자열을 넣어도 결국에는 베이스 조건에 도달하게 될 것이다.

4단계. 조합

부분 답을 가지고 전체 답을 구하는 방법을 생각해본다.

먼저, 베이스 조건 바로 윗단계를 생각해보자.

베이스 조건이 문자열 길이가 0과 1일 때였으니, string 길이가 2일 때를 가정한다.
“hi”가 인풋으로 들어왔다. 답은 무엇인가? “ih”다.

아랫 단계의 재귀 호출에서 반환되는 값은 무엇인가?

우리는 문자열에서 앞의 한 글자를 빼는 방식으로 분해하기로 했다. 그러니까 아랫단계의 재귀 호출은 reverseString(”i”)가 된다. “i”를 반환한다.

부분 답을 가지고 어떻게 현재 답을 만들까? 즉, “i”를 가지고 어떻게 “ih”를 만들까?

아랫 단계 재귀 호출에서 나온 결과값 뒤에 “h”를 더해주면 될 거 같다.

두번째, 베이스 조건 3단계 위를 생각해보자.

이 문제에서는 String 길이가 4인 경우다.
주어진 문자열이 “gray”라고 해보자. 답은 당연히 “yarg”다.

“gray”의 바로 아랫단계 답은 무엇인가?
앞 글자를 하나 떼고 “ray”를 집어넣었을 것이다. “yar”가 나와야 한다.

여기서 우리는 믿어 본다. 진짜 이 함수가 “yar”를 return하는지 생각하지 말자. 일단 그렇다고 치자.

더 중요한 것은 “yar”가 결과값으로 나왔을 때, 어떻게 조합을 해야 현재 답인 “yarg”가 나오냐는 거다.

이것도 쉽다. “yar” + “g”를 해주면 된다.

두 조합의 공통점

이 2가지 조합을 생각해보니, 일반화할 수 있는 규칙이 보인다.

부분 문제의 답에, 현재 문자열의 첫글자를 붙여준다.

그러면 “hi”를 넣었을 때 “i” + “h”를 반환한다.
“gray”를 넣었을 때 “yar” + “g”를 반환한다.

이제 재귀 함수 설계가 끝났다!

여기서 하나 더 생각해보자.

조합을 완성하고 보니, 굳이 베이스 조건은 2개나 필요하지 않다는 걸 알 수 있다.

문자열 길이가 1인 경우, 부분문제의 답에 현재 문자열의 첫글자를 붙여주면 된다. 굳이 별도로 베이스 조건을 설정해주지 않아도 우리가 원하는 답이 나온다.

따라서 문자열 길이가 1인 경우의 베이스 조건은 지워도 문제가 없다.

이렇게 베이스 조건은 나중에 분해나, 조합을 완성하고 나서 조절할 수 있다.

4단계를 모두 생각해보았다.

재귀가 꼭 필요한가? NO (이지만 YES라고 가정하자)
베이스 조건? String 길이 0일 때 → 빈 배열
분해? reverseString(맨 앞 글자 하나 뺀 문자열)
조합? 부분 문제의 답 + 인풋값 문자열의 "맨 앞 글자"

이제 코드로 작성하면 이렇게 된다.

// written in Swift
func reverseString(s: String) {
    // 베이스 조건	
    if s.count == 0 { return "" }
    // 분해 + 조합
    return reverseString(s.dropfirst()) + s.first!
}

아주 우아한 재귀 코드를 써냈다!

실행 순서와 결과값 자세히 보기

실제로 “Hello”를 넣었을 때 이 함수의 실행 순서와 결과값은 이렇게 된다.

// 분해한 부분 문제의 결과값
Each call: str === "?"        	  -> reverseString(str.subst(1)) + str.charAt(0)
1st call – reverseString("Hello") -> reverseString("ello")       + "h"
2nd call – reverseString("ello")  -> reverseString("llo")        + "e"
3rd call – reverseString("llo")   -> reverseString("lo")         + "l"
4th call – reverseString("lo")    -> reverseString("o")          + "l"
5th call – reverseString("o")     -> reverseString("")           + "o"

// 결과값
5th call will return reverseString("") + "o" = "o"
4th call will return reverseString("o") + "l" = "o" + "l"
3rd call will return reverseString("lo") + "l" = "o" + "l" + "l"
2nd call will return reverserString("llo") + "e" = "o" + "l" + "l" + "e"
1st call will return reverserString("ello") + "h" = "o" + "l" + "l" + "e" + "h"

저 간단한 함수로, 어떤 문자열이든 우아하게 뒤집어놓을 수 있다.

하지만 다시 한번 강조하고 싶은 것은, 알고리즘 문제를 풀려고 할 때 이걸 머릿속으로 그리려 하면 안 된다. 재귀적으로 생각하지 않아야 재귀가 쉽게 풀린다.

베이스 조건, 분해, 조합을 따로 따로 잘 설계했다면, 알아서 저렇게 잘 작동할 것이라고 믿으면 된다.

2. 링크드 리스트 합치기 (Merge Linked Lists)

문제

오름차순으로 정렬되어있고, 값의 중복이 가능한 링크드 리스트, list1과 list2가 주어진다.
이 2개의 리스트를 하나의 정렬된 리스트로 합치고, head를 return 하라.
단, 새로운 리스트를 만들지 않고 기존 리스트 중 하나를 변형해야 한다.

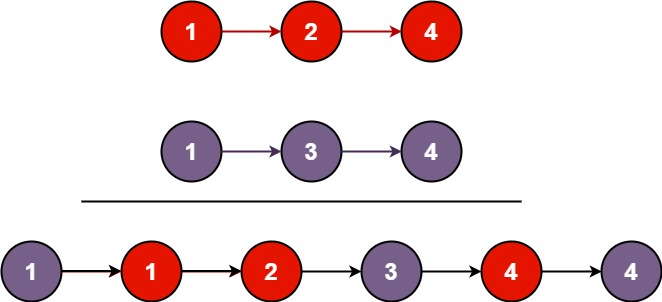
Input: list1 = [1,2,4], list2 = [1,3,4]
Output: [1,1,2,3,4,4]

(출처: leetcode)

1단계. 재귀를 꼭 써야하는가?

반복이 아니라 굳이 재귀로 풀어야 하는 문제일까?

링크드 리스트는 재귀적인 자료 구조다. 재귀를 쓰면 깔끔하게 풀 수 있을 거 같다.

2단계. 베이스 조건

답을 바로 알 수 있는 가장 간단한 상황은 무엇일까?

링크드 리스트 길이가 0이나 1일 때를 생각해보자.

이 경우 문제에서 즉각 답을 알 수 있는 가장 단순한 상황은 3가지다.

list1, list2의 길이가 둘 다 0일 때 (값이 nil일 때)
→ 둘 다 빈 리스트이므로, nil이 답
둘 중 한쪽의 길이가 0일 때 (list1 혹은 list2가 nil일 때)
→ nil이 아닌 리스트가 답
둘 다 길이가 1일 때
→ 값이 더 작은 리스트의 뒤에 값이 더 큰 리스트를 붙이면 답

이렇게 두고 다음 단계로 넘어가보자.

3단계. 분해

재귀 호출을 거듭하면서 베이스 케이스에 가까워지도록 인풋값을 조작한다.
어떻게 하면 인풋으로 주어지는 링크드 리스트의 길이가 0으로 가게 할 수 있을까?

링크드 리스트의 포인터를 사용해 현재 노드 바로 뒤의 노드를 집어넣어주면 될 것 같다.

링크드 리스트가 [1,2,4]로 주어진다면, [2,4] → [4] → [] 이렇게 작아지게 될 것이다.
그러면서도 여전히 정렬된 리스트라는 인풋의 조건은 만족한다.

즉, 인자에 list1.next list2.next 를 넣어주면 결국 베이스 조건으로 가까워질 것이다.

4단계. 조합

부분 답을 가지고 전체 답을 구하는 방법을 생각해본다.

베이스 조건에서 한 단계 위를 생각해보자.

둘 다 길이가 1일 때를 베이스 조건으로 잡아두었다.

분해는 리스트의 다음 노드를 넣어주기로 했다.

하지만 인풋값이 2개다보니 분해를 하는 여러 방법이 있다.
어떤 쪽 리스트를 다음 노드로 넣어줄지는 정하지 않았다.

list1.next만 인자로 넣거나, list2.next만 인자로 넣을 수도 있다.
둘 다 분해한다면 list1.next , list2.next 를 같이 넣으면 된다.

일단 한번 해보자.
한쪽 리스트의 길이가 2이고, 다른 한 쪽 리스트의 길이가 1일 때를 생각해보자.

list1이 [1,3], list2가 [2]라고 가정해본다.

list1만 분해해주었다.
list1은 [3]이 되고, list2는 [2]가 된다. 답은 [2,3]이 된다.
list2만 분해해주었다.
list1은 [1,3]이 되고, list2는 []가 된다. 답은 [1,3]이 된다.
둘 다 분해를 해주었다.
list1은 [3], list2는 []가 된다. 베이스 조건에 걸린다. 답은 [3]이 된다.

각각의 경우에 분해해서 나온 결과값을 가지고, 어떻게 [1,2,3]을 만들 수 있을까?

방법 1) list1만 분해

list1만 분해하면, [2,3]이라는 결과값이 나왔다.

그러면 여기서 list1을 분해하면서 떼어냈던 [1] 노드를 맨 앞에 붙여준다.
우리가 원하는 답 [1,2,3]이 나온다.

방법 2) list2만 분해

결과값이 [1,3]이 나왔다.

우리는 [1,2,3]이 필요한데, 결과값이 [1,3]이어서 순서가 자연스럽지 않다. 간단하게 답을 만들어낼 수가 없다. list2만 분해하면 안 될 것 같다.

list2만 분해한 경우가 자연스럽지 않은 이유는, list2의 head 값이 list1의 head 값보다 크기 때문이다.

만약 list1이 [2,3]이고, list2가 [1]이었다면, list2를 분해하는 경우가 자연스럽다.

즉, 한쪽만 분해를 할 때는, head값이 더 작은 쪽을 분해해줘야 한다는 걸 알 수 있다.

방법 3) list1과 list2를 둘 다 분해

list1과 list2를 다 분해하면, 결과값으로 [3]이 나왔다.

이때 list1과 list2에서 떼어냈던 [1], [2] 노드 값을 비교한다.

정렬 순서를 유지해야 한다. 더 작은 노드가 앞에 오고, 뒤의 노드가 뒤에 오고, 그 다음 아랫단계의 결과값이 오도록 리스트를 합쳐야 한다.

if list1.val < list2.val {
    list2?.next = mergeTwoLists(list1.next, list2.next)
    list1?.next = list2
}

...잠깐, 근데 이 경우는 결과값이 맨 뒤에 와도 된다.
하지만 인풋값이 바뀌면 순서가 달라질 수 있지 않을까?

만약 list1이 [1,2]이고, list2가 [5]라면 어떨까?

그러면 분해했을 때 결과가 [2]가 나온다.

그러면 list1 + mergeTwolists() + list2 순서로 붙여줘야 [1, 2, 5]가 나오게 된다.

이 문제를 해결하기 위해서 결과값과 list2를 한번 더 비교할 수도 있다. 3개를 비교해서 더 작은 순서로 리스트를 합쳐준다. 이런 식으로.

if list1.val < list2.val {
    if list2.val < mergeTwoLists(list1.next, list2.next) {
        list2?.next = mergeTwoLists(list1.next, list2.next)
        list1?.next = list2
    }
}

하지만 하나만 분해하는 방식에 비해서 너무 번거롭다. 이 분해 방식은 제껴두고, 더 작은 쪽을 분해하는 방식으로 가자.

베이스 조건에서 3단계 위를 생각해보자.

우리는 더 작은 쪽을 분해하는 방식을 선택하기로 했다. 이제 조금 더 복잡한 인풋값을 가정한다.

list1이 [1,2,4]이고, list2가 [2,3]이라고 생각해보자. 3번 분해를 거치면 베이스 조건에 도달하는 인풋값이다. 베이스 조건에서 3단계 위다.

손으로 풀어보자.
list1이 [1,2,4]이고, list2가 [2,3]라면 답은 [1,2,2,3,4]가 돼야 한다.

바로 아랫 단계의 답은 무엇일까?
더 작은 쪽을 분해하기로 했으니, list1.next, list2를 인자로 넣어 호출했을 것이다.
[2,4]와 [2,3]이 들어갔을 때 답은 무엇이 돼야 하는가?

여기서 또 다시 재귀 호출을 머릿속에 그리면 안 된다. 그냥 정답을 손으로 풀자.
[2,2,3,4]다. 일단 구현을 하지 않았어도 그 답이 나왔다고 믿어보자.

자, list1이 [1,2,4]이고, list2가 [2,3]인 상황에서, 아랫단계의 결과값은 [2,2,3,4]가 나왔다. 그러면 어떻게 [1,2,2,3,4]가 되게 할까?

간단하다. 분해할 때 떼어냈던 [1] 노드를 앞에 붙여주면 된다. 아까 베이스 조건 바로 윗단계와 똑같다는 걸 알 수 있다.

조합의 공통점 찾기

베이스 조건 바로 윗단계 (list1 = [1,3], list2 = [2]),
베이스 조건 3단계 위 (list1 = [1,2,4]이고, list2 = [2,3]),

두 경우 모두 일반화할 수 있는 규칙이 보인다.

분해할 때 떼어냈던 [1] 노드, 즉 더 작은 값을 가진 노드를 재귀 호출 결과값 앞에 붙여주면 된다.

이제 재귀 설계를 마쳤으니 코드를 써보자!

func mergeTwoLists(_ list1: ListNode?, _ list2: ListNode?) -> ListNode? {
    // 베이스 조건 1. list1, list2의 길이가 둘 다 0일 때
    if list1 == nil && list2 == nil { return nil }

    // 베이스 조건 2. 둘 중 한쪽의 길이가 0일 때
    if list1 == nil { return list2 }
    if list2 == nil { return list1 }

    // 베이스 조건 3. 둘 다 길이가 1일 때
    if list1?.next == nil && list2?.next == nil {
        if list1!.val < list2!.val {
            list1?.next = list2
            return list1
        } else {
            list2?.next = list1
            return list2
        }
    }
    
    // 분해: 자기 자신을 호출하면서, 더 Head의 값이 작은 리스트에서 head를 떼내고 넣어줌.
    // 조합: 그 결과값의 앞에 떼어냈던 head를 붙이고, 그 head를 반환함.
    if list1!.val <= list2!.val {
        list1?.next = mergeTwoLists(list1?.next, list2)
        return list1
    } else {
        list2?.next = mergeTwoLists(list2?.next, list1)
        return list2
    }
}

이 코드는 모든 테스트를 통과한다. 정답!

불필요한 베이스 조건 지우기

그렇지만 좀 더 욕심이 난다. 코드를 더 줄일 수 없을까?

베이스 조건을 다시 한번 보자.

list1, list2의 길이가 둘 다 0일 때 (값이 nil일 때)
→ 둘 다 빈 리스트이므로, nil이 답
둘 중 한쪽의 길이가 0일 때 (list1 혹은 list2가 nil일 때)
→ nil이 아닌 리스트가 답
둘 다 길이가 1일 때
→ 값이 더 작은 리스트의 뒤에 값이 더 큰 리스트를 붙이면 답

잘 보면 1번째 베이스 조건과, 3번째 베이스 조건은 필요없다는 걸 알 수 있다.

1번째 베이스 조건: 둘 다 길이가 0인 경우

둘 다 0인 경우는 어차피 2번째 조건에도 마찬가지로 해당된다.
1번째 조건 없이 2번째 베이스 조건으로만 실행해도, 다른 한쪽 리스트를 반환하게 되어있고, 그 리스트는 비어있다. 따라서 똑같이 비어있는 리스트(nil)을 반환한다.

3번째 베이스 조건: 둘 다 길이가 1인 경우

둘 다 1인 경우, 한번 더 분해를 하게 되면 두 번째 조건에 해당한다.
두 번째 베이스 조건으로 실행한다. 실행한 그 결과값을 '조합'하면 값이 더 작은 노드 뒤에 값이 더 큰 리스트를 붙인 리스트가 된다.
결과값은 지금 있는 코드와 똑같다.

따라서 1번째와 3번째 베이스 조건은 없어도 그대로 잘 작동한다.

깔끔하게 정리된 코드는 다음과 같다.

func mergeTwoLists(_ list1: ListNode?, _ list2: ListNode?) -> ListNode? {
    // 베이스 조건 2. 둘 중 한쪽의 길이가 0일 때
    if list1 == nil { return list2 }
    if list2 == nil { return list1 }

    // 분해: 자기 자신을 호출하면서, 더 Head의 값이 작은 리스트에서 head를 떼내고 넣어줌.
    // 조합: 그 결과값의 앞에 떼어냈던 head를 붙이고, 그 head를 반환함.
    if list1!.val <= list2!.val {
        list1?.next = mergeTwoLists(list1?.next, list2)
        return list1
    } else {
        list2?.next = mergeTwoLists(list2?.next, list1)
        return list2
    }
}