Merge Sort

eden6187·2021년 7월 12일

알고리즘

목록 보기

15/20

Merge sort의 목적

정렬을 위한 알고리즘이다.

Merge sort의 핵심 아이디어

정확한 설명은 아니지만, 나는 다음과 같이 이해했다.

더이상 자를 수 없을때까지 2개로 자르고, 더 이상 자를 수 없을 경우 각각의 문제들을 병합한다.

아마, 이해가 잘 가지 않을 것이다. 그림을 보면 더 직관적으로 이해 할 수 있다.

그림에 나온 숫자들의 의미를 정확하게 이해 할 수 있다면 병합 정렬의 수행 과정을 완벽하게 이해 했다고 볼 수 있다. 만약 그림에 있는 숫자가 헷갈린다면, 재귀적인 구조를 이해 했다고 보기는 힘들다.

재귀적인 구조를 가장 쉽게 이해 할 수 있는 예제가 전위/중위/후위 순회라고 생각한다. 다음 글을 참고하면 기억을 되새겨 보는데 큰 도움이 될 것이다. 각각의 순회 알고리즘의 재귀 함수 호출 사이에서 visit()이 언제 호출 되는지 생각해보면 된다.

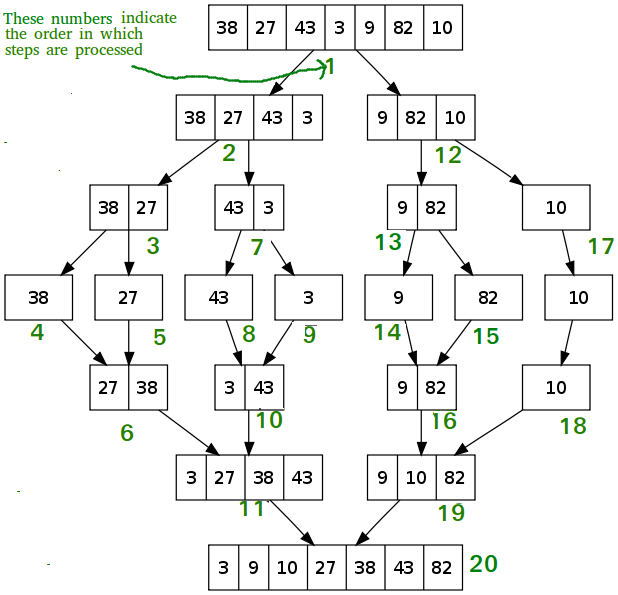
Merge sort의 동작 원리

병합 정렬은 크게 3가지 단계로 나뉜다.

N짜리 배열을 N/2짜리 2개의 배열로 자른다.( divide )
각각의 배열에 대하여 재귀적으로 합병 정렬을 수행한다.( recursion )
재귀적으로 병합 정렬이 수행 된 N/2의 문제들을 병합한다. ( conquer )

이런 형태의 문제 해결 방식을 가지는 알고리즘을 분할 정복 알고리즘이라 한다.

분할 하는 것 자체는 그다지 어렵지 않지만, 분할 한 2개의 배열을 병합하는 과정이 좀 헷갈릴 것이다.

그렇다면, 바킹독 님의 강의를 참고하자.

Merge sort의 장점

병합 정렬의 가장 큰 장점으로는 stable sort 라는 점이다.

하지만, 구현을 잘못 하면 이러한 Merge Sort의 장점을 놓치게 될 수 있으니 장점을 살리기 위해서는 이 점에 유의해야 한다.

아래의 코드의 주석 부분 중에서 [1]로 표시해 놓은 부분을 잘 보자!

즉, 2개의 배열을 Merge할 때 크기가 같은 배열이 있다면, 앞쪽에 있는 값을 먼저 병합을 위한 배열에 넣어주어야 한다.

병합 정렬이 stable sort라는 특징을 잘 살리면 다음과 같은 응용이 가능하다.

만약, 이름을 기준으로 사전식 정렬을 하되, 같은 이름을 가진 사람 중에서는 나이가 적은 순으로 정렬 하고자 한다면

나이를 기준으로 오름차순으로 정렬하고
이름을 기준으로 사전식 정렬을 수행해주면 된다.

이렇게 stable sort의 장점을 활용한 응용 방식도 알아 두는 것이 좋다.

이 부분 역시 바킹독 님의 강의에 나오는 부분이다.

    public void merge(int[] src, int left, int right){
        int mid = (left + right) / 2; // left ~ mid 포함.
        int[] tmp = new int[right - left + 1];

        int leftPtr = left; // 왼쪽 절반짜리 배열의 시작점
        int rightPtr = mid + 1; // 오른 절반짜리 배열의 시작점
        int tmpPtr = 0;

        while(leftPtr < mid + 1  && rightPtr < right + 1){
            int leftValue = src[leftPtr];
            int rightValue = src[rightPtr];

            if(leftValue <= rightValue) { // [1] - 이 부분에서 등호가 빠진다면, 정렬은 되지만, in-place sort 가 아니게 된다.
                tmp[tmpPtr] = leftValue;
                leftPtr++;
            }
            else {
                tmp[tmpPtr] = rightValue;
                rightPtr++;
            }
            tmpPtr++;
        }

        while(leftPtr < mid + 1){
            tmp[tmpPtr++]  = src[leftPtr++];
        }

        while (rightPtr < right + 1){
            tmp[tmpPtr++]  = src[rightPtr++];
        }

        for(int i = 0 ; i < tmp.length; i++){
            src[left + i] = tmp[i];
        }

        return;
    }