[ 백준 12100 - 2048 (easy) ]

문제 분석

1. 조건에 맞게 블록을 합치는 방법
2. 상하좌우에 대해서 다른 코드를 짜주는것이 아니라 보드 자체를 회전 시킨다는 아이디어를 생각해 내는 것이 중요했던것 같다. 상하좌우로 블록을 합치는 코드를 모두 구현 할 수 는 있었겠지만 디버깅이 너무 오래걸리고 구현 시간이 너무 오래 걸려서 실전에서는 사용할 수 없을것 같다.
3. 알고리즘 자체 보다는 문제를 다른 시각으로 바라 볼 수 있는 능력이 중요함을 알려주는 문제였다.

시간 복잡도

• 4^5 : 5번 합치는 방향을 고려함.
• 각각의 방향에 대해서 합침 : 20 x 20 x 3(최대 3번 회전) x 5( 5개의 방향 )
  1024 x 20 x 20 x 3 x 5 = 약 600만
  각각의 경우에 대해서 최댓값 구하는 것을 생각해도 1억을 넘기기는 힘들다.

구현

블록을 왼쪽으로 합치기

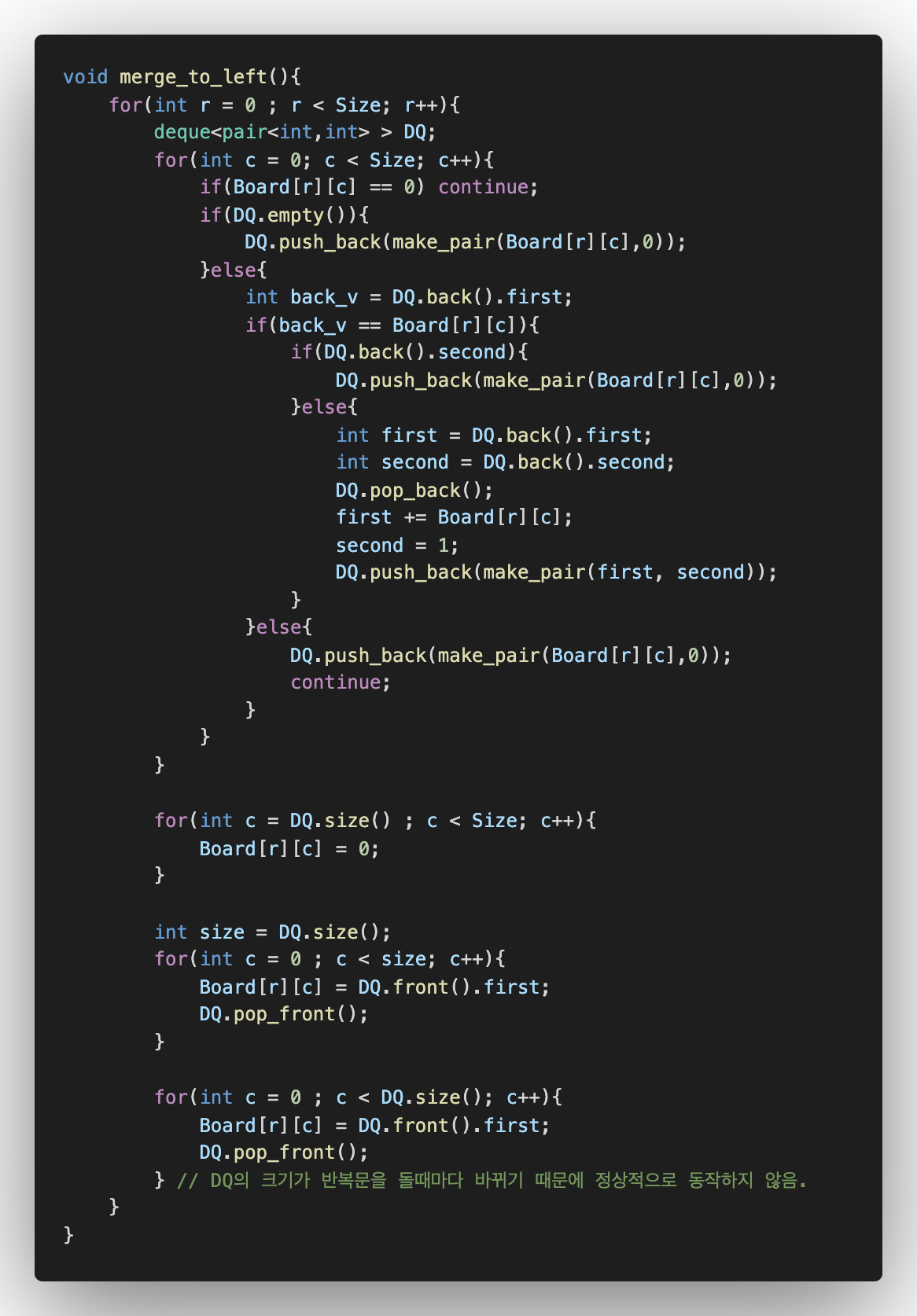
deque를 사용해서 구현했다. 코드가 보기에는 매우 난잡하지만 알고리즘 자체는 매우 간단하다.

헤맸던 부분

1. 2차원 배열을 회전하고 하나의 방향으로 합쳐주는 방법을 생각하지 못했다.
   모든 방향에 대해서 합쳐주는 코드를 따로 구현하려다 보니 시간이 너무 오래 걸렸다.
2. 덱을 사용하다 아래와 같은 치명적인 실수를 했다.

덱 / 스택 / 큐 / 벡터등 크기가 동적으로 변할 수 있는 자료 구조들을 이용해서 반복문을 돌릴때는 덱의 사이즈의 변화가 반복문에 어떤 영향을 주고 있는지 주의 깊게 확인해야 한다는 교훈을 느꼈다. 별거 아닌 실수지만 자칫 잘못하면 실전에서는 시간을 꽤 많이 잡아 먹을 것 같다.

얻은 것

새로운 알고리즘을 학습했다기 보다는 문제를 새롭게 보면 더 간단한 해결 방법이 나올 수도 있다는 사실을 깨달았다.

전체 코드

#include <iostream>
#include <stack>
#include <vector>
#include <deque>

using namespace std;

int Board[22][22];
int Board_copy[22][22];

void init(){
    ios::sync_with_stdio(0);
    cin.tie(0);
}

int Size;

void get_input(){
    cin >> Size;
    for(int i = 0 ; i < Size; i++){
        for(int ii = 0 ; ii < Size; ii++){
            int input;
            cin >> input;
            Board[i][ii] = input;
            Board_copy[i][ii] = input;
        }
    }
}

void return_to_origin(){
    for(int i = 0 ; i < Size; i++){
        for(int ii = 0 ; ii < Size; ii++){
            Board[i][ii] = Board_copy[i][ii];
        }
    }
}

void print_board(){
    cout << "start print board \n";
    for(int i = 0 ; i < Size; i++){
        for(int ii = 0 ; ii < Size; ii++){
            cout << Board[i][ii] << " ";
        }
        cout << "\n";
    }
    cout << "end print board \n";
}

void merge_to_left(){ 
    for(int r = 0 ; r < Size; r++){
        deque<pair<int,int> > DQ;
        for(int c = 0; c < Size; c++){
            if(Board[r][c] == 0) continue;
            if(DQ.empty()){
                DQ.push_back(make_pair(Board[r][c],0));
            }else{
                int back_v = DQ.back().first;
                if(back_v == Board[r][c]){
                    if(DQ.back().second){
                        DQ.push_back(make_pair(Board[r][c],0));    
                    }else{
                        int first = DQ.back().first; 
                        int second = DQ.back().second;
                        DQ.pop_back();
                        first += Board[r][c];
                        second = 1;
                        DQ.push_back(make_pair(first, second));
                    }
                }else{
                    DQ.push_back(make_pair(Board[r][c],0));
                    continue;
                }
            }
        }

        for(int c = DQ.size() ; c < Size; c++){
            Board[r][c] = 0;
        }

        int size = DQ.size();
        for(int c = 0 ; c < size; c++){
            Board[r][c] = DQ.front().first;
            DQ.pop_front();
        }

        for(int c = 0 ; c < DQ.size(); c++){
            Board[r][c] = DQ.front().first;
            DQ.pop_front();
        } // DQ의 크기가 반복문을 돌때마다 바뀌기 때문에 정상적으로 동작하지 않음.
    }
}

void rotate_90_cw(){

    int tmp[22][22];

    for(int r = 0 ; r < Size; r++){
        for(int c = 0 ; c < Size; c++){
            tmp[c][Size - r - 1] = Board[r][c];
        }
    }

    for(int r = 0 ; r < Size; r++){
        for(int c = 0 ; c < Size; c++){
            Board[r][c] = tmp[r][c];
        }
    }

}

void merge(int dir){
    for(int i = 0 ; i < dir; i++){
        rotate_90_cw();
    }
    merge_to_left();
}

vector<int> rotation_case;
void rotate(){
    for(int i = 0 ; i < 5; i++){
        merge(rotation_case[i]);
    }
}

int get_max(){
    int ans  = Board[0][0];
    for(int r = 0; r < Size; r++){
        for(int c = 0 ; c < Size; c++){
            ans = max(ans,Board[r][c]);
        }
    }
    return ans;
}


int ans = 0;
void func(int cnt){
    if(cnt == 5){
        return_to_origin();
        rotate();
        ans = max(ans, get_max());
        return;
    }

    for(int i = 0 ; i < 4; i++){
        rotation_case.push_back(i);
        func(cnt + 1);
        rotation_case.pop_back();
    }
}

int main(){
    init();
    get_input();
    func(0);
    cout << ans << "\n";
    return 0;
}

참조

위 설명에서 사용된 이미지와 설명의 일부는 바킹독님의 유트브와 바킹독님의 블로그의 강의내용과 강의 자료에서 발췌하였습니다.