[ 백준 2193 - 이친수 - Java ]

문제 분석

DP

시간 복잡도

DP를 이용하면 O(N)에 해결 가능

구현

1. 테이블 정의

long[][] T = new long[100+1][2+1];
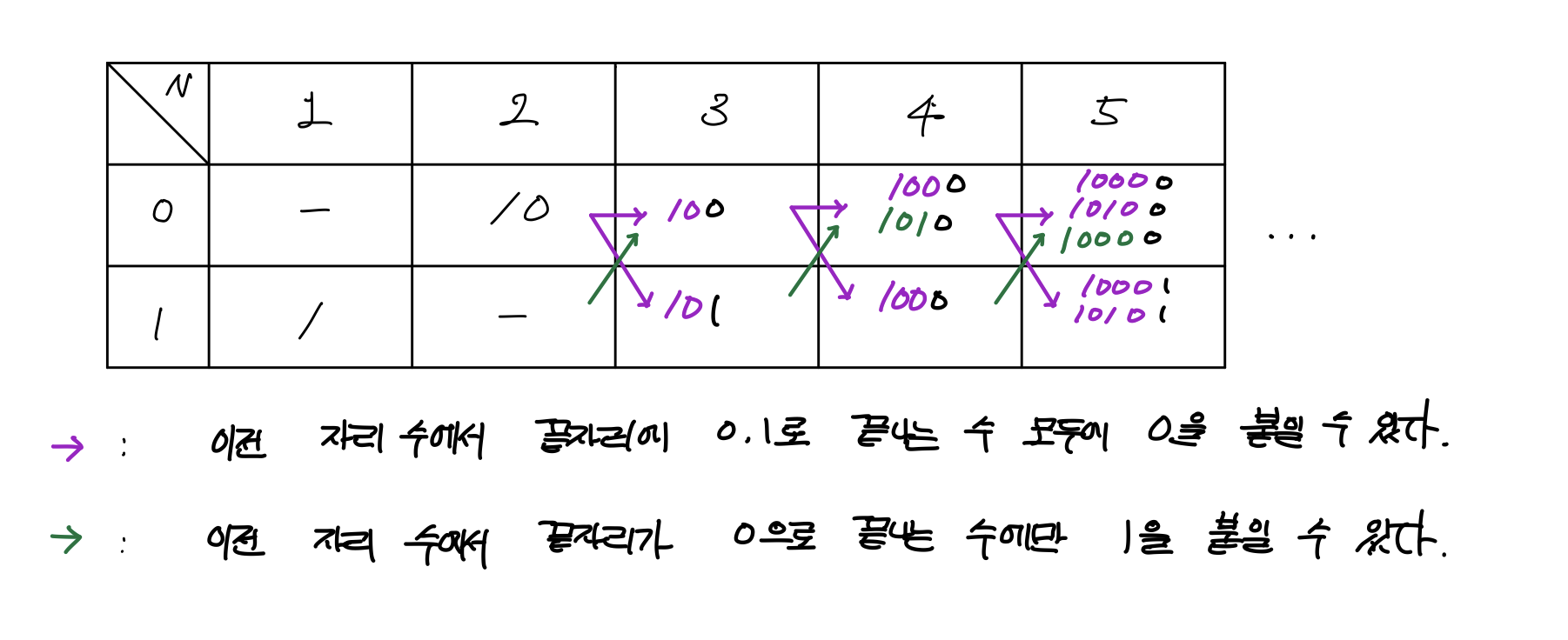
// T[N][1] -> N번째 자리 수 중에서 마지막이 1로 끝나는 이친수.
// T[N][0] -> N번째 자리 수 중에서 마지막이 0으로 끝나는 이친수.

2. 점화식 구하기

for(int n = 3; n <= N; n++){
	T[n][0] = T[n-1][0] +T[n-1][1];
    //  n-1번째 자리 수에서 끝자리가 0,1로 끝나는 수 모두에 0을 붙여서 n번째 자리 수를 만들 수 있다.
	T[n][1] = T[n-1][0];
    //  n-1번째 자리 수에서 끝자리가 0으로 끝나는 수에만 1을 붙여서 n번째 자리 수를 만들 수 있다.
}

3. 초기값 설정

T[1][1] = 1;
T[1][0] = 0;

T[2][1] = 0;
T[2][0] = 1;

헤맸던 부분

자료형 선택을 잘못했습니다. long을 사용 했어야 했는데 int를 사용 했습니다.

다른 접근 방법

테이블을 만약, T[N] : N번째 자리 수의 이친수의 갯수라고 정의한다면, T[N] = T[N-1] + T[N-2]가 된다.

T[N-1] : N-1번째 자리 수의 뒤에 모두 '0'을 붙여서 N번째 자리의 이친수를 만들 수 있음.
T[N-2] : N-2번째 자리 수의 뒤에 모두 '01'을 붙여서 N번째 자리의 이친수를 만들 수 있음.

즉, 피보나치 수열이랑 유사한 형태의 점화식을 구할 수 있습니다.

얻은 것

DP에 대한 감을 잃지 않기.

전체 코드 [ 내 코드 - Java ]

내 java 코드

느낀점

문제를 풀면서 로직은 맞는거 같은데 자꾸 틀려서 어디서 틀린지 한참을 고민했습니다.

결국 해답을 볼 수 밖에 없었고 제가 int형 자료형을 사용했기에 틀렸다는 것을 알 수 있었습니다.

점화식을 보고 일반항을 도출해서 자료형의 크기를 유추 할 수 있겠지만 제가 과연 실전에서 이렇게까지 할 수 있을지는 의문입니다.

실전에서 이런 문제를 받았을 때 자료형 선택에 문제가 있다는 것을 쉽게 캐치해내기는 어렵겠지만 정말 제 로직이 완벽한데 틀리는 경우 자료형의 문제인지 의심해 보는 것도 고려해 보아야 한다는 교훈을 얻었습니다.

참조

문제 출처