문제 유형
- DFS
- 스택
시간 복잡도
시간 복잡도가 그리 중요하지는 않은 문제였다. 자료구조 수업 시간에 배웠던 스택을 이용한 수식 계산과 DFS에 대해서 이해하고 있다면 그리 어렵지 않은 문제였다.
구현
1. 우선 순위 설정 (DFS)
public void dfs(int curDepth){ if(curDepth == 3) { setPriority(); long temp = calc(tokenize(expression)); if(temp > answer) answer = temp; return; } for(int i = 0; i < 3; i++){ if(isUsed[i]) continue; isUsed[i] = true; priority[curDepth] = opt[i]; dfs(curDepth + 1); isUsed[i] = false; } }
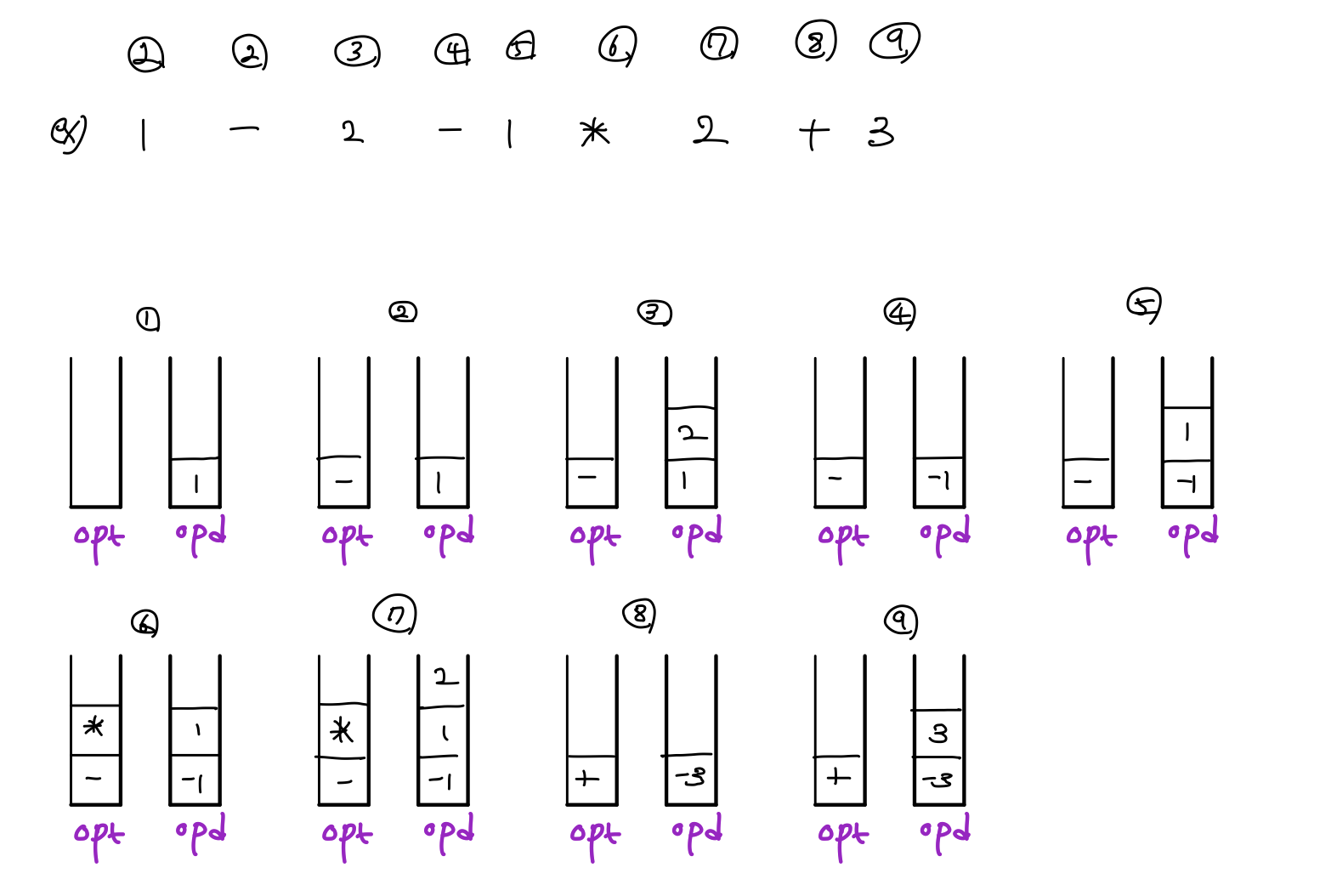
2. 문제열을 계산을 위한 토큰으로 만들기
public ArrayList<String> tokenize(String expression){ ArrayList<String> tokens = new ArrayList<>(); int left = 0; for(int i = 0 ; i < expression.length(); i++){ if(isOpt(expression.charAt(i))){ String subStringOpd = expression.substring(left,i); tokens.add(subStringOpd); String subStringOpt = expression.substring(i,i+1); tokens.add(subStringOpt); left = i + 1; } } tokens.add(expression.substring(left, expression.length())); return tokens; }
3. 토큰들을 이용해서 우선순위에 맞게 수식 계산하기
public long calc(ArrayList<String> tokens){ int result = 0; Stack<Long> opdStack = new Stack<>(); Stack<String> optStack = new Stack<>(); for (String token : tokens) { if(!isOpt(token)){ opdStack.push(Long.valueOf(token)); continue; } while(!optStack.isEmpty() // 스택이 비어 있거나 && priorities.get(token.toCharArray()[0]) <= priorities.get(optStack.peek().toCharArray()[0])) // 현재 보고 있는 연산자의 우선순위가 stack의 top보다 높을 경 { long opd1 = opdStack.pop(); long opd2 = opdStack.pop(); Character opt = optStack.pop().toCharArray()[0]; long temp = 0; switch (opt){ case '+': temp = opd2 + opd1; opdStack.push(temp); break; case '-': temp = opd2 - opd1; opdStack.push(temp); break; case '*': temp = opd2 * opd1; opdStack.push(temp); break; } } optStack.push(token); } while(!optStack.isEmpty()){ long opd1 = opdStack.pop(); long opd2 = opdStack.pop(); char opt = optStack.pop().toCharArray()[0]; long temp = 0; switch (opt){ case '+': temp = opd2 + opd1; opdStack.push(temp); break; case '-': temp = opd2 - opd1; opdStack.push(temp); break; case '*': temp = opd2 * opd1; opdStack.push(temp); break; } } return opdStack.peek() > 0 ? opdStack.peek() : opdStack.peek() * (-1); }
헤맸던 부분
우선순위에 따라서 수식을 계산 하는 부분을 구현하는 것이 시간이 많이 걸렸다
처음에 알고리즘을 명확하게 세우지 않고 바로 구현에 들어가다 보니 코드 자체가 매우 지저분해졌다.
가장 헤맸던 부분은 연산자를 만났을 경우에 대한 처리이다.
연산자를 스택에 쌓기전에 우선 순위에 맞게 스택에 연산자를 쌓을 수 있는지를 생각해보아야 한다.
스택을 이용해서 최종적인 결과를 구할 것이기 때문에 스택은 항상 다음과 같은 형태를 가져야 한다.
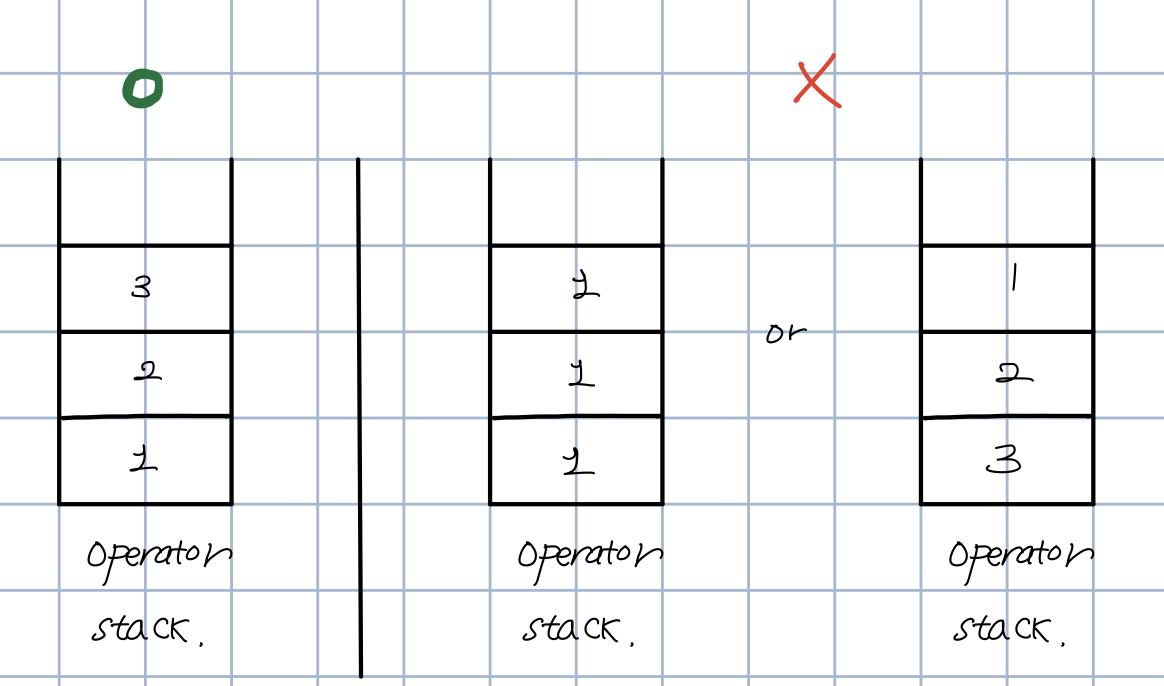
왼쪽과 같이 위에 쌓이는 연산자의 우선순위가 아래에 있는 연산자의 우선순위보다 커야 한다. 같거나 작으면 안된다. 오른쪽과 같이 스택에 연산자가 쌓이게 되면 나중에 스택에서 위에서 하나씩 연산자를 빼서 최종 결과를 구할 때 우선순위가 낮은 연산자들이 먼저 계산 되기 때문에 올바른 결과를 얻을 수 없다.
거의 다 왔다. 앞에서 한 말을 정리해보면 스택에 새로운 연산자가 쌓일 수 있는 조건은
- 스택이 비어있거나
- 혹시 존재한다면 스택의 top에 있는 연산자의 우선순위가 새로운 연산자의 우선순위보다 낮을 경우이다.
이를 수도 코드로 나타내 본다면
if ( stack.isEmpty() or stack.top().priority < newOperator.priority ) stack.push(newOperator)위의 조건을 만족하지 않는 동안은 연산자 1개, 피연산자 2개를 스택에서 뽑아서 계산을 해준 뒤 결과 값을 다시 피연산자 스택에 넣어주어야 한다. 따라서 드모르간의 법칙을 이용해서
"stack.isEmpty() or stack.top().priority < newOperator.priority"
의 부정을 취해서
"!stack.isEmpty() and stack.top().priority >= newOperator.priority"
의 조건을 while문에 넣어주면 된다.
처음 접하면 복잡하기 때문에 이해가 잘 가지 않지만
결국에는 스택에서 먼저 빠질 연산자들이 우선순위가 높아야지만 올바른 결과를 구할 수 있기 때문에 그에 맞게 스택에 연산자를 순서대로 쌓아준다고 생각하면 된다.
얻은 것
스택을 이용한 중위 표현식 계산
전체 코드 [ 내 코드 ]
import java.util.*;
class Solution {
String expression;
public long solution(String expression) {
this.expression = expression;
dfs(0);
return answer;
}
HashMap<Character, Integer> priorities = new HashMap<>();
boolean[] isUsed = {false, false, false};
char[] opt = {'+', '-', '*'};
int[] priority = {2,1,3};
public void setPriority(){
int i = 0;
for (char c : opt) {
priorities.put(c, priority[i]);
i++;
}
}
long answer = 0;
public void dfs(int curDepth){
if(curDepth == 3) {
setPriority();
long temp = calc(tokenize(expression));
if(temp > answer) answer = temp;
return;
}
for(int i = 0; i < 3; i++){
if(isUsed[i]) continue;
isUsed[i] = true;
priority[curDepth] = opt[i];
dfs(curDepth + 1);
isUsed[i] = false;
}
}
public boolean isOpt(Character ch){
return ch.equals('*') || ch.equals('-') || ch.equals('+');
}
public boolean isOpt(String ch){
return ch.equals("*") || ch.equals("-") || ch.equals("+");
}
public ArrayList<String> tokenize(String expression){
ArrayList<String> tokens = new ArrayList<>();
int left = 0;
for(int i = 0 ; i < expression.length(); i++){
if(isOpt(expression.charAt(i))){
String subStringOpd = expression.substring(left,i);
tokens.add(subStringOpd);
String subStringOpt = expression.substring(i,i+1);
tokens.add(subStringOpt);
left = i + 1;
}
}
tokens.add(expression.substring(left, expression.length()));
return tokens;
}
public long calc(ArrayList<String> tokens){
int result = 0;
Stack<Long> opdStack = new Stack<>();
Stack<String> optStack = new Stack<>();
for (String token : tokens) {
if(!isOpt(token)){
opdStack.push(Long.valueOf(token));
continue;
}
while(!optStack.isEmpty() // 스택이 비어 있거나
&& priorities.get(token.toCharArray()[0]) <= priorities.get(optStack.peek().toCharArray()[0])) // 현재 보고 있는 연산자의 우선순위가 stack의 top보다 높을 경
{
long opd1 = opdStack.pop();
long opd2 = opdStack.pop();
Character opt = optStack.pop().toCharArray()[0];
long temp = 0;
switch (opt){
case '+':
temp = opd2 + opd1;
opdStack.push(temp);
break;
case '-':
temp = opd2 - opd1;
opdStack.push(temp);
break;
case '*':
temp = opd2 * opd1;
opdStack.push(temp);
break;
}
}
optStack.push(token);
}
while(!optStack.isEmpty()){
long opd1 = opdStack.pop();
long opd2 = opdStack.pop();
char opt = optStack.pop().toCharArray()[0];
long temp = 0;
switch (opt){
case '+':
temp = opd2 + opd1;
opdStack.push(temp);
break;
case '-':
temp = opd2 - opd1;
opdStack.push(temp);
break;
case '*':
temp = opd2 * opd1;
opdStack.push(temp);
break;
}
}
return opdStack.peek() > 0 ? opdStack.peek() : opdStack.peek() * (-1);
}
}느낀점
느낀점들
