23.09.06 최초 작성

1. 덧셈과 뺄셈

• 두 연산의 결과를 64비트 이내에 표현할 수 없는 경우가 생기는데 이를 오버플로우라고 한다.
• 다른 부호를 가진 수의 덧셈의 경우 오버플로우가 발생하지 않는다.
• 같은 부호를 가진 수의 뺄셈의 경우 오버플로우가 발생하지 않는다.
• 두 양수를 더했을 때 sign 비트가 1일 경우 오버플로우가 발생한 것이다.
• 음수에서 어떠한 값을 뺏을 때 sign 비트가 0인 경우 오버플로우가 발생한 것이다.

2. 곱셈

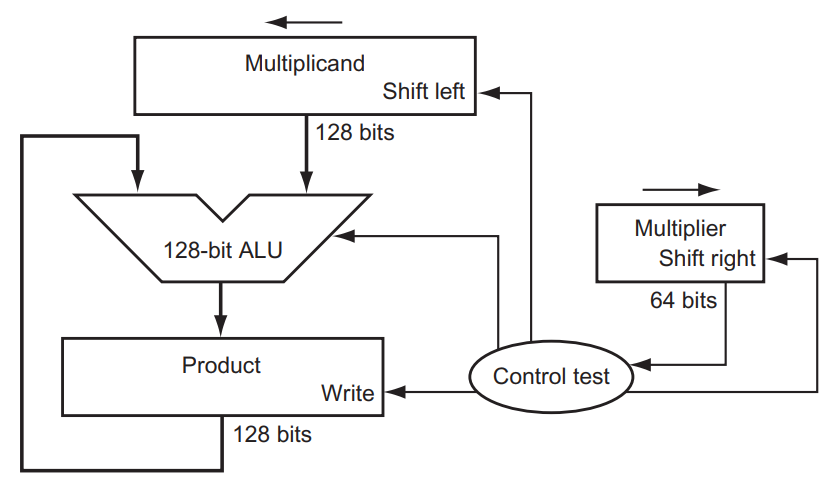
• multiplicand (피승수) : 첫 번째 피연산자

• multiplier (승수) : 두 번째 피연산자

• product (곱) : 최종 결과

  1. 승수의 LSB를 검사한다.
     • 0이면 continue
     • 1이면 현재까지 계산된 '곱'에 피승수를 더한다.
  2. 피승수를 왼쪽으로 1칸 shift 한다.
  3. 승수를 오른쪽으로 1칸 shift 한다.
  4. 이 과정을 반복한다.

3. 나눗셈

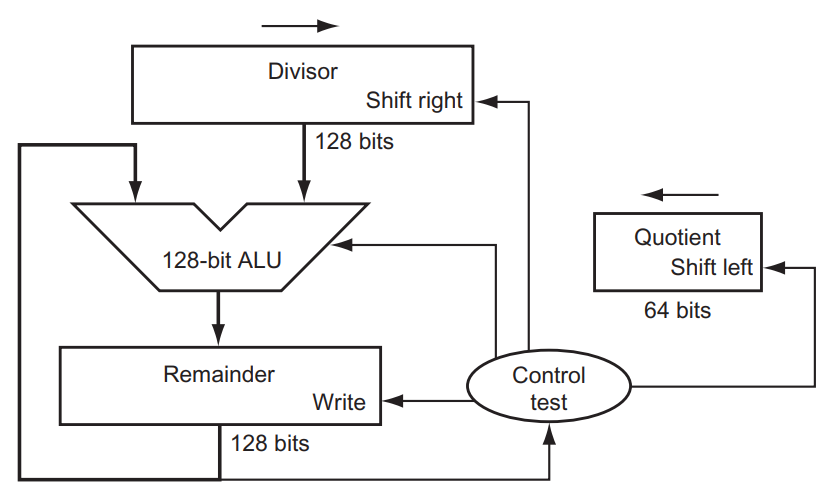
• dividend (피제수) : 첫 번째 피연산자

• devisor (제수) : 두 번째 피연산자

• quotient (몫) : 최종 결과

  1. 피제수에서 제수를 뺀 값을 검사한다.
     • 남은 값이 0보다 크면 '몫'을 왼쪽으로 1칸 shift 하고 오른쪽 비트는 1로 둔다.
     • 남은 값이 0보다 크면 다시 제수를 더해주고 '몫'을 왼쪽으로 1칸 shift 하고 오른쪽 비트는 0으로 둔다.
  2. 제수를 오른쪽으로 1칸 shift 한다.
  3. 이 과정을 반복한다.

4. 부동소수점

이진법을 통해 소수점 자리를 표현하기 위해 고안된 방법. 소수부분과 지수부분으로 나누어 표현하며 다음과 같은 형태를 가진다.

$(1+F) \;\times \;2^y$

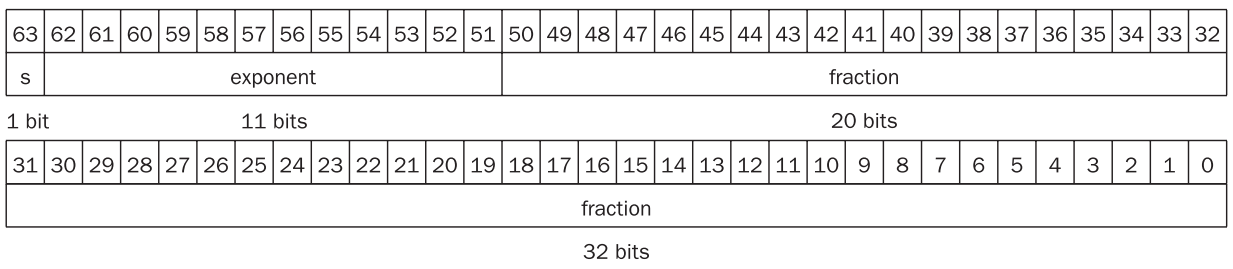
비트 영역은 다음과 같다.

32bit ($2.0\;\times\;10^{-38}$~ $2.0\;\times\;10^{38}$)

64bit ($2.0\;\times\;10^{-308}$~ $2.0\;\times\;10^{308}$)