문제

Min Stack은 기존 Stack과 거의 동일하지만 getMin() 메소드가 존재한다. getMin() 메소드는 현재까지 스택에 쌓인 값 중에 최소값을 리턴하는 함수이다.

문제는 Min Stack의 push(), pop(), top(), getMin() 메소드를 $O(1)$의 시간복잡도 갖도록 구현하는 것이다.

첫번째 풀이

이 문제를 풀 때 Java에서 지원하는 Stack 자료구조를 사용하지 않고 간단하지만 직접 구현하였다. 값은 배열(stack)에 저장하고 top 변수를 두어 인덱스를 관리하였다. 이 때, getMin() 메소드를 구현할 때 시간복잡도 $O(1)$을 갖추기 위해 값을 저장하는 배열을 2차원으로 선언했다. 배열의 첫번째 인덱스는 들어온 순서이고 두번째 인덱스는 값과 최소값을 저장하기 위한 인덱스다.

stack[top][0] = 가장 최근에 들어온 value
stack[top][1] = 최근 value까지의 최솟값

Stack에 값을 push할 때 [input value, minimum value]인 길이가 2인 배열이 저장된다. 그리고 getMin은 stack의 top 인덱스의 두번째 인덱스 즉 stack[top][1]을 리턴하면 최솟값이 된다. 그 외 나머지 메소드들의 구현은 배열로 스택을 구현하는 기존과 거의 동일하다.

class MinStack {

    private static final int MAX_SIZE = 30000;
    private int[][] stack = new int[MAX_SIZE + 1][2];
    private int top = -1;


    public MinStack() {
    }
    
    public void push(int val) {
        int min = top == -1 ? val : Math.min(stack[top][1], val);
        stack[++top][0] = val;
        stack[top][1] = min;
    }
    
    public void pop() {
        top--;
    }
    
    public int top() {
        return stack[top][0];
    }
    
    public int getMin() {
        return stack[top][1];
    }
}

이렇게 모든 메소드의 시간복잡도를 $O(1)$로 구현하였고 결과는 다음과 같다.

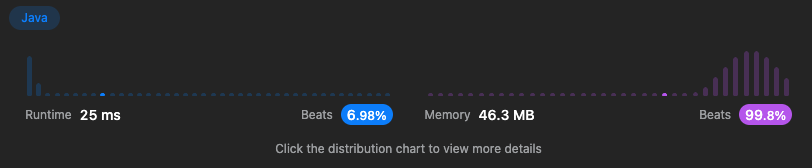
시간복잡도가 $O(1)$임에도 실행속도가 최하위로 나왔다. 이를 개선하기위해 다른 방식으로 다시 풀어보았다.

두번째 풀이

두번째 풀이는 다른 방법으로 최솟값을 관리했다. 첫번째 풀이는 새로운 값과 최솟값을 같이 저장해 유지했다면 이번 풀이는 또 다른 스택 배열로 관리한다. 값을 push할 때 최솟값을 관리하는 배열은 다음과 같은 과정을 수행한다.

// push 메소드

// 값을 저장하는 stack 배열과 동일한 minStack 배열을 생성한다.
// minStack[minTop]은 stack[top]과 같아지기 전까지 stack에 push된 값중 최솟값이된다.
int[] minStack = new int[stack.length]; 

// 값의 인덱스를 나타내는 top과 동일한 역할을 minStack에서 하는 minTop을 생성하고 -1로 초기화한다.
int minTop = -1; 

// minTop == -1 이면 minStack에 값을 push한다.
if (minTop == -1) minStack[++minTop] = value;

// minTop != -1 이면 minStack[minTop]과 value를 비교해 value가 더 낮은 경우 push한다.
else if (minStack[minTop] >= value) minStack[++minTop] = value;

이 때, 마지막 과정에 minStack[minTop]의 값이 value보다 같거나 클 때 push 해야한다.

minStack[minTop]은 stack[top]과 같아지기 전까지 stack에 push된 값중 최솟값이된다. 따라서 값을 pop할 때는 대상이 되는 stack[top]의 값이 최솟값이면 minStack도 하나 빼준다. 그래야 pop된 이후에도 최솟값을 유지할 수 있다.

// pop 메소드

if (stack[top] == minStack[minTop]) minTop -= 1;

push(3), push(5), push(2), pop()의 과정을 따라가보면 다음과 같다.

1. push(3)
top = 0,	stack = [3, 0, 0, 0, ...]
minTop = 0,	minStack = [3, 0, 0, 0, ...]

2. push(5)
top = 1,	stack = [3, 5, 0, 0, 0, ...]
minTop = 9,	minStack = [3, 0, 0, 0, ...] // 3이 5보다 작으므로 5는 넣지 않는다.

3. push(2)
top = 2,	stack = [3, 5, 2, 0, 0, 0, ...]
minTop = 1,	minStack = [3, 2, 0, 0, 0, ...]

4. pop()
top = 1,	stack = [3, 5, 0, 0, 0, ...] // 2가 빠져 0으로 표현했지만 실제 배열은 변화없다.
minTop = 0,	minStack = [3, 0, 0, 0, ...] // 2가 최솟값이므로 같이 pop한다. 위와 마찬가지로 실제 배열은 변함 없다.

3번 과정까지 스택까지 최솟값이 2임을 알 수 있으며 이와 동일한 값이 minStack[minTop]에 저장되어 있다. 4번 과정에서 pop()을 하면 기존의 최솟값인 2가 빠지고 3이 최솟값이 된다. 이 때, minStack에서도 하나 빼 최솟값이 3이 됨을 알 수 있다.

전체 코드는 다음과 같다.

class MinStack {

    private static final int MAX_SIZE = 30000;
    private int[] stack = new int[MAX_SIZE + 1];
    private int[] minStack = new int[MAX_SIZE + 1];
    private int top = -1, minTop = -1;


    public MinStack() {
    }
    
    public void push(int val) {
        stack[++top] = val;
        
        if (minTop == - 1 || minStack[minTop] >= val) {
            minStack[++minTop] = val;
        }
    }
    
    public void pop() {
        if (stack[top] == minStack[minTop]) {
            minTop--;
        }
        top--;
    }
    
    public int top() {
        return stack[top];
    }
    
    public int getMin() {
        return minStack[minTop];
    }
}

마찬가지로 모든 메소드의 시간복잡도는 $O(1)$로 구현되었다. 실행 결과는 25ms → 4ms까지 낮아졌다.

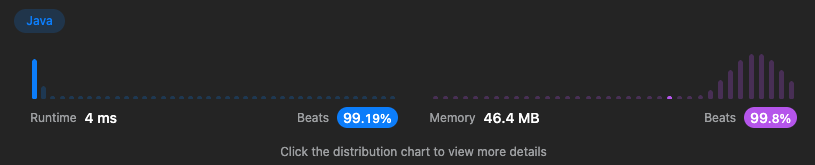
나는 같은 배열을 쓰기 때문에 크게 성능 차이가 없을 거라고 생각했다. 하지만 1차원 배열이 2차원 배열보다 접근 속도가 빠르다고 한다. 그 이유는 다차원 배열은 메모리 상에서 세로 인덱스(첫번째 풀이에서 값의 인덱스 == top과 같은)를 읽을 때 건너 뛰어야하는 메모리 블록이 많은 반면 1차원 배열은 바로 옆에 있기 때문에 오버헤드가 없다는 것이다.

또한, 성능의 차이가 발생하는 이유 중 하나로 대입연산이 두번째보다 첫번째 풀이에 많기 때문이라고 생각한다. 첫번째 풀이에서는 매 push마다 최솟값을 같이 대입한다. 컴퓨터의 성능에 따라 차이가 있겠지만 내 컴퓨터로 천만번과 오백만번의 대입연산을 했을 때 차이가 있었다.

• 1차원 배열일 때: 천만번 → 7ms, 5백만번 → 5ms
• 2차원 배열일 때: 천만번 → 28ms, 5백만번 → 7ms

이 결과로 2차원 배열일 때 차이가 더 큰 것으로 보아 위 두 이유가 첫번째 풀이가 실행시간이 훨씬 느리게 나온 원인인 것 같다.