문제

오름차순으로 정렬된 배열에서 두 원소를 골라 더한 값이 target이 되는 두 인덱스를 찾는 문제이다. 예를들어 numbers = [2,7,11,15], target = 9이라면 2 + 7이 target인 9가 되기 때문에 [1, 2]를 리턴하면 된다. 또한 반드시 공간복잡도를 $O(1)$로 풀어야한다.

풀이

가장 쉽게 풀 수 있는 방법은 다음과 같다.

for (i = 0; i < numbers.length - 2; i++)
	for (j = i + 1; j < numbers.length - 1; j++)
    	if numbers[i] + numbers[j] == target
        then return [i + 1, j + 1]

하지만 이 풀이는 시간복잡도 $O(n^2)$으로 효율이 좋지 않다.

이 문제의 포인트는 배열이 오름차순으로 정렬되어 있다는 것이다. 따라서 Two Pointer를 사용할 수 있다. left번째 원소와 right 원소의 합과 target을 비교하여 left 증가 또는 right 감소를 통해 답을 구할 수 있다.

1. numbers[left] + numbers[right] > target

• 두 원소의 합이 target보다 크다면 right를 감소시킨다. 배열은 오름차순으로 정렬되어 있기때문에 left를 증가시키더라도 target보다 큰 값이 된다.

2. numbers[left] + numbers[right] < target

• 두 원소의 합이 target보다 작다면 left를 증가시킨다. right를 감소시켜봤자 두 원소의 합은 더 작아진다.

3. numbers[left] + numbers[right] == target

• [left + 1, right + 1]을 return 한다.

left = 0, right = numbers.lenght - 1
while (left < right)
	sum = numbers[left] + numbers[right]
    
    if sum < target then left++
    else if sum < target then right--
    else return [left + 1, right + 1]

이를 코드로 작성하면 다음과 같다.

class Solution {
    public int[] twoSum(int[] numbers, int target) {
        int left = 0, right = numbers.length - 1;
        int[] answer = new int[2];

        while (left < right) {
            int sum = numbers[left] + numbers[right];

            if (sum < target) {
                left++;
            } else if (sum > target) {
                right--;
            } else {
                answer[0] = left + 1;
                answer[1] = right + 1;
                break;
            }
        }

        return answer;
    }
}

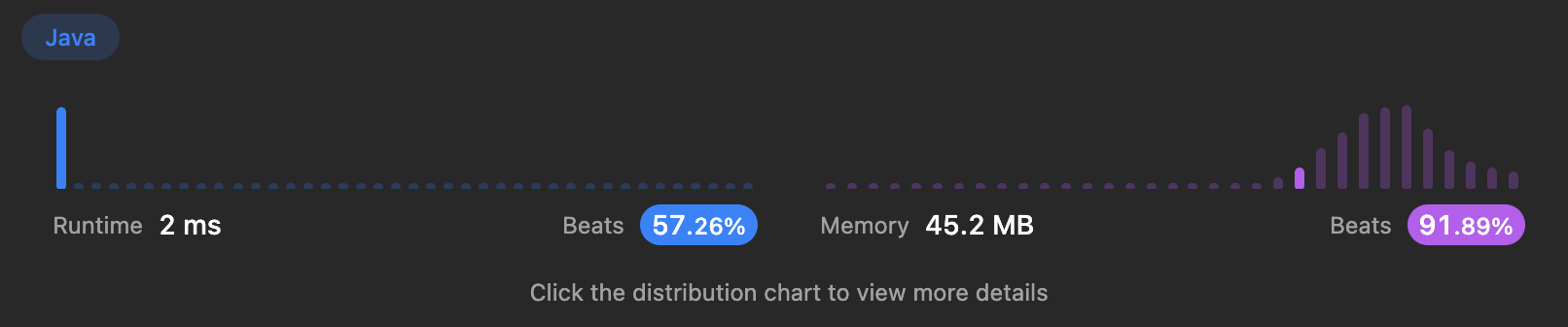
이 풀이의 시간복잡도는 $O(n)$이며 공간복잡도는 $O(1)$이다.

개선하기

한 테스트는 정확히 1개의 답을 갖고 있다.(The tests are generated such that there is exactly one solution.) 따라서 반복문의 조건을 numbers[left] + numbers[right] != target으로 하면 코드를 좀 더 간소화 시킬 수 있다.

class Solution {
    public int[] twoSum(int[] numbers, int target) {
        int left = 0, right = numbers.length - 1;
        while (numbers[left] + numbers[right] != target) {
            if (numbers[left] + numbers[right] < target) {
                left++;
            } else right--;
        }

        return new int[] {left + 1, right + 1};
    }
}

다른 Solution 확인..

다른 Solution들도 대부분 이와 같은 Two Pointer를 사용해 풀이했다. Two Pointer를 사용한 방법이 시간복잡도 $O(n)$이며 공간복잡도는 $O(1)$로 가장 적절한 풀이인 것같다.