문제

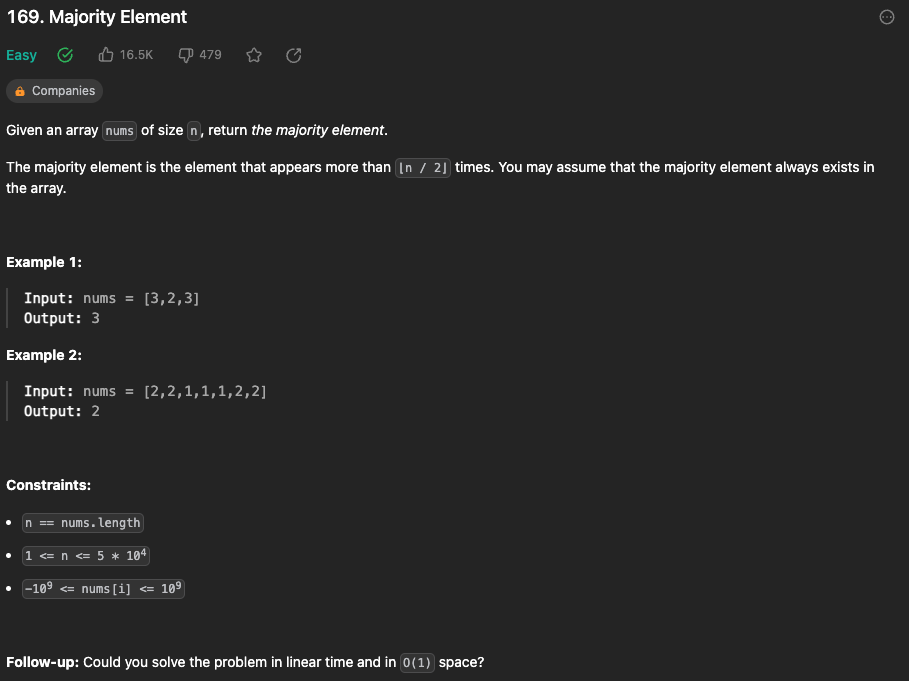
길이가 n인 nums 배열에서 n / 2번 이상 나온 element를 Majority Element라고 한다. nums 배열에서 Majority Element를 찾는 것이 문제이다.

첫 풀이

Follow-up에서 나온 것처럼 시간복잡도를 $O(n)$, 공간복잡도를 $O(1)$로 풀어보고 싶었지만 공간복잡도를 만족시킬만한 아이디어가 떠오르지 않았다. 따라서 nums배열에 나온 값들의 개수를 모두 카운팅하여 가장 높은 카운트의 키 값을 리턴하도록 하였다.

이 과정에서 시간을 조금이라도 줄여보고자 left와 right 변수를 사용하여 양쪽 끝부터 동시에 탐색을 시작해 탐색 횟수를 반으로 줄이려고 하였다.

import java.util.*;

class Solution {

    public int majorityElement(int[] nums) {
        Map<Integer, Integer> count = new HashMap<>();

        int left = 0, right = nums.length - 1;
        while (left <= right) {
            count.put(nums[left], count.getOrDefault(nums[left], 0) + 1);

            if (left != right) {
                count.put(nums[right], count.getOrDefault(nums[right], 0) + 1);
            }

            left += 1;
            right -= 1;
        }

        int majority = 0;
        for (Map.Entry<Integer, Integer> entry : count.entrySet()) {
            if (entry.getValue() > nums.length / 2) {
                majority = entry.getKey();
                break;
            }
        }

        return majority;
    }
}

이 문제에서 $-10^9$ <= nums[i] <= $10^9$이기 때문에 카운팅을 배열로하는 것은 옳지 않다. 따라서 Map을 사용하였다. 공간복잡도와 시간복잡도는 모두 $O(n)$로 공간복잡도 결과만 낮게 나올 것이라고 예상했지만 결과는 전혀 달랐다.

오히려 공간복잡도가 상위권이며 시간복잡도는 하위권이었다.

두번째 풀이

혹시나 majority를 구하는 과정에서 entrySet을 사용하지 않고 count를 구하면서 기준인 n / 2보다 크면 해당 값을 리턴하도록 하면 시간이 줄지 않을까하고 개선해보았다.

import java.util.*;

class Solution {

    public int majorityElement(int[] nums) {
        Map<Integer, Integer> count = new HashMap<>();

        int majority = 0;
        int standard = nums.length / 2;
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int leftCount = count.getOrDefault(nums[left], 0) + 1;
            count.put(nums[left], leftCount);

            int rightCount = 0;
            if (left < right) {
                rightCount = count.getOrDefault(nums[right], 0) + 1;
                count.put(nums[right], rightCount);
            }

            if (leftCount > standard || rightCount > standard) {
                majority = leftCount > standard ? nums[left] : nums[right];
                break;
            }

            left += 1;
            right -= 1;
        }

        return majority;
    }
}

하지만..

첫 풀이와 거의 다를바 없었다.

세번째 풀이

이번에는 거의 완전히 새롭게 시도해보았다. 2중 for문을 사용해 방문하지 않은 원소에 대해 개수를 세며 majority element라면 탐색을 중단하도록 구현하였다. 이 과정에서 한 번 개수를 세어놨던 원소는 다시 셀 필요가 없으므로 Set을 사용해 방문 여부를 관리하였다.

import java.util.*;

class Solution {

    public int majorityElement(int[] nums) {
        Set<Integer> visit = new HashSet<>();

        int answer = 0;
        for (int i = 0; i < nums.length; i++) {
            if (visit.contains(nums[i])) {
                continue;
            }

            visit.add(nums[i]);

            int count = 1;
            for (int j = i + 1; j < nums.length; j++) {
                if (nums[i] == nums[j]) {
                    count += 1;
                }
            }

            if (count > nums.length / 2) {
                answer = nums[i];
                break;
            }
        }

        return answer;
    }
}

공간복잡도는 위 풀이들과 달라지지 않지만 시간복잡도는 $O(n^2)$이 되기때문에 실행시간에서 더 느릴 것이라 예상하였지만 첫 풀이의 1/10에 해당하는 2 ms가 나왔다.

세번째 풀이가 가장 빠른 이유가 무엇일까?

시간복잡도는 첫 2개의 풀이가 선형시간으로 빠르다. 하지만 마지막 풀이가 결과적으로 가장 빠르다. 또한, Set 의 conatins()와 add() 함수는 내부적으로 HashMap의 함수를 사용하기 때문에 더욱이 첫 2개의 풀이가 더 빨라야할 것 같다.

나의 추측으로는 HashMap.put() 함수를 사용하는 횟수때문에 그럴 것같다. 세번째 풀이에서는 방문하지 않은 경우에만 put() 함수를 사용한다(HashSet.add()는 내부적으로 HashMap.put()을 사용한다). 하지만 첫 2개의 풀이에서는 n번 모두 HashMap.put() 함수를 사용하기 때문에 더 느린 것이라고 생각한다.

시간복잡도 $O(n)$, 공간복잡도 $O(1)$로 푸는 방법은?

첫번째, 두번째 풀이에서나마 시간복잡도를 $O(n)$을 달성했지만 세번째 풀이까지 공간복잡도를 $O(1)$로 만들지 못하였다. Solution을 보고 알게된 방법은 과반수 투표 알고리즘을 사용하는 것이다. 문제에서 n / 2보다 큰 것이 majority element이므로 적용하기에 좋은 알고리즘이다.

과반수 투표 알고리즘은 배열 내 과반수가 넘는 원소가 존재한다면 결과 값은 항상 과반수 원소가 된다. 여기에서 자세한 설명을 찾아볼 수 있었다. 과반수 투표 알고리즘은 과반수 원소를 찾는데 시간복잡도 $O(n)$, 공간복잡도 $O(1)$로 월등히 뛰어나다.

class Solution {
    public int majorityElement(int[] nums) {
        int majority = 0;
        int count = 0;
        for (int i = 0; i < nums.length; i++) {
            if (count == 0) {
                majority = nums[i];
            }
            
            if (majority == nums[i]) {
                count += 1;
            } else {
                count -= 1;
            }
        }

        return majority;
    }
}

공간복잡도가 가장 뛰어난 방법임에도 불구하고 실제 제출한 결과로는 가장 안좋게 나왔다.. 왜지..?

이 외에도..

Solution에는 내가 생각하지 못한 방법이 또 존재했었다. 시간복잡도가 $O(nlogn)$이지만 정렬을 이용한 방법이 있다. 이 방법은 nums배열을 정렬했을 때 majority에 해당하는 요소의 개수는 과반수가 넘으므로 이 값은 항상 배열의 중간에 위치하게 된다. 따라서 nums[n / 2]의 값이 majority가 된다.