문제

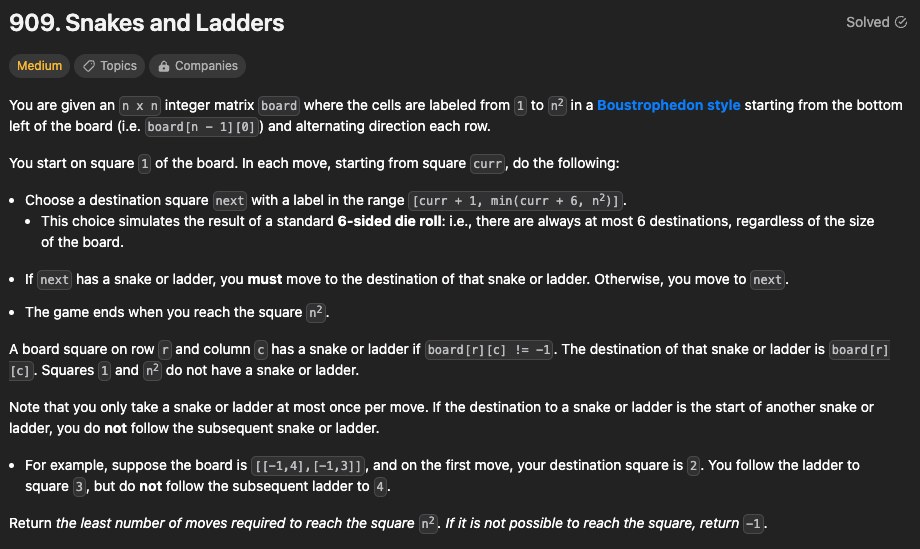
n*n의 board에 대한 정보가 주어진다. 각 cell은 다음과 같은 방식으로 번호가 매겨진다.

...
16	15	14	13
9	10	11	12
8	7	6	5
1	2	3	4

왼쪽 아래부터 1번이며 ㄹ 형태로 번호가 이어져있다. 문제는 다음과 같다.

1번 cell부터 시작해 n*n 번호 cell까지 가는데 던지는 최소 주사위 횟수를 구하는 것이다. 주사위이기 때문에 현재 cell에서 갈 수 있는 다음 cell들은 [현재+1 ~ min(현재+6, n*n)]번 cell이 된다. 또한 다음 cell에 사다리 또는 뱀이 있을 경우 반드시 이어진 곳으로 이동해야한다.

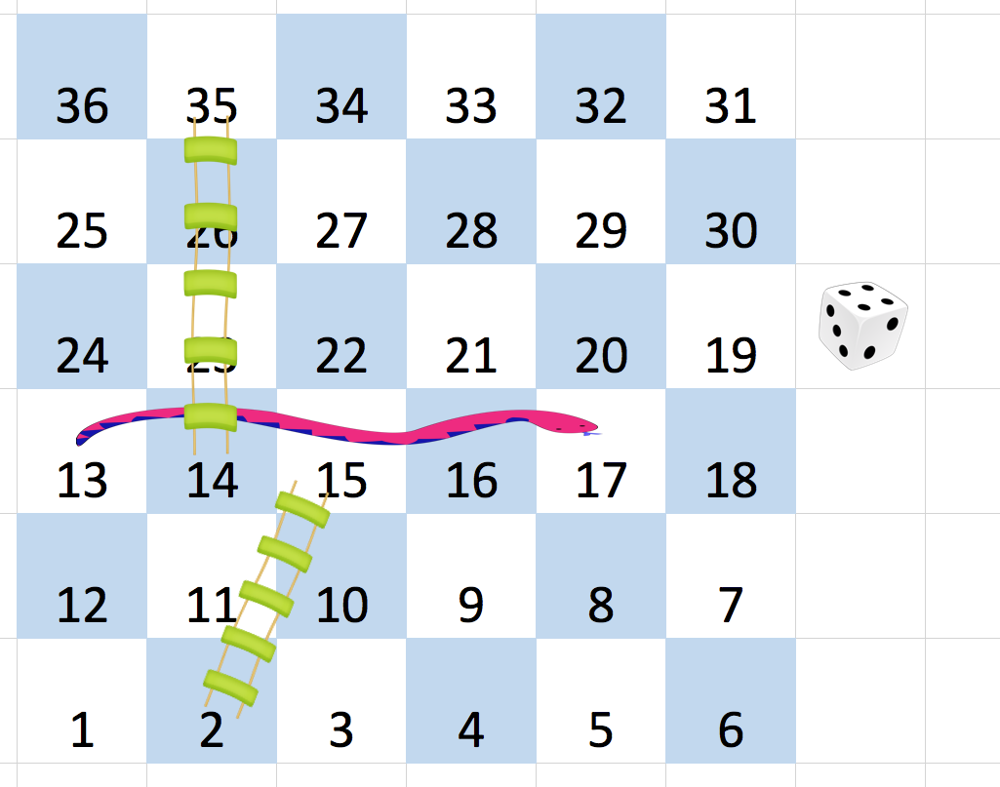이미지 출처: LeetCode

풀이

보통 최단거리를 구하는 문제에서 BFS를 많이 사용한다. 너비 우선 탐색이기 때문에 시작지점부터 탐색을 시작했을 때 목적지가 탐색이 되면 그것이 최단거리이기 때문이다. 이 문제는 던지는 최소 주사위 횟수이지만 같은 개념으로 BFS로 풀이가 가능하다.

먼저 시작지점을 1번 cell을 넣고 시작한다. BFS를 수행하며 [cell+1 ~ min(cell+6, n*n)]번 셀을 탐색하고 큐에 넣는다. 이때 다음 cell이 -1이 아닌 경우 사다리 또는 뱀이므로 이어진 cell 번호를 큐에 넣는다.

BFS는 cell 번호를 기준으로 수행하기 때문에 해당 번호에 사다리 또는 뱀이 존재하는지 확인을 위해 좌표로 바꾸어 주어야한다. 이를 위해 getCoordinate(cell번호) 함수를 구현했다.

이 과정에서 방문 처리가 중요하다. 예를 들어, a → b로 이어지는 사다리가 있고 b → c 이어지는 뱀이 존재할 때 a를 방문했을 때 c까지가 아닌 b까지만 이동해야한다. 따라서 이동한 cell이 사다리 또는 뱀이면 해당 cell의 방문은 찍어주지 않고 이어진 cell의 방문을 찍어주어야 한다.

구현 코드는 다음과 같다.

class Solution {

    private int size;

    public int snakesAndLadders(int[][] board) {
        this.size = board.length;

        Queue<Integer> queue = new ArrayDeque<>();
        boolean[] visit = new boolean[size * size + 1];
        queue.add(1);
        visit[1] = true;

        int turn = 0;
        while (!queue.isEmpty()) {
            int queueSize = queue.size();
            turn++;
            while (queueSize-- > 0) {
                int now = queue.poll();

                for (int i = 1; i <= 6; i++) {
                    int next = now + i;
                    if (next > size * size) {
                        break;
                    }

                    int[] pos = getCoordinate(next);
                    if (board[pos[0]][pos[1]] != -1) {
                        next = board[pos[0]][pos[1]];
                    }

                    if (next == size * size) {
                        return turn;
                    }

                    if (visit[next]) {
                        continue;
                    }

                    queue.add(next);
                    visit[next] = true;
                }
            }
        }

        return -1;
    }

    private int[] getCoordinate(int cellNumber) {
        int y = (size - 1) - ((cellNumber - 1) / size);
        int x;

        if (size % 2 == 0) {
            x = y % 2 == 0 ?
                (size - 1) - (cellNumber - 1) % size :
                (cellNumber - 1) % size;
        } else {
            x = y % 2 == 0 ?
                (cellNumber - 1) % size :
                (size - 1) - (cellNumber - 1) % size;
        }

        return new int[] {y, x};
    }
}

실행시간은 4ms로 상위권에 속하지만 메모리 사용량은 중간에 위치한다. 좌표를 구하고 int[]를 리턴하기 때문에 이 과정에서 메모리를 더 사용하는 것으로 생각된다.

이 문제를 풀이하면서 오래 걸렸던 부분은 ㄹ자 형태로 매겨진 번호에서 해당 번호에 대한 좌표를 구하는 것이다. 다른 Solution 들에서 이런 복잡도를 낮추기 위해 board를 2차원에서 1차원으로 바꿔 푸는 경우도 많았다.