"힙이랑도 조금은 겹치는 것 같은..."
구간 트리(Segment Tree)
In computer science, a segment tree, also known as a statistic tree, is a tree data structure used for storing information about intervals, or segments.
위키백과에 정리되어 있는 구간 트리에 대한 설명입니다. 간만에 개념에 대한 번역조차 되어있지 않은 자료를 만나게 되었네요. 위의 내용을 간략하게 번역해보면 이렇습니다.
컴퓨터 과학에서 통계 트리라고도 알려진 구간 트리란, 구간(intervals) 또는 구분(segments) 에 관한 정보를 저장하기 위한 트리 자료 구조이다.
원어민이 아니라 대체 intervals 와 segments 가 어떤 유의미한 차이를 보이는지는 잘 모르겠습니다만, 기본적으로 중요한 지점은 구간 트리가 트리 자료 구조라는 것입니다. 그 중에서도 이진 트리 구조를 지니고 있죠.
힙(또는 힙트리)이 여러 개의 값 중에서 가장 크거나 작은 값을 빠르게 찾기 위한 이진 트리라면, 구간 트리는 특정한 구간에서의 가장 크거나 작은 값, 또는 구간의 합을 효율적으로 검색할 수 있는 이진 트리입니다.
특정 구간의 최소값을 구하는 단순한 알고리즘이 O(N) 의 시간 복잡도를 지닌다면 구간 트리는 이진 탐색과 비슷하게 구간을 반씩 쪼개어 만들기 때문에 O(logN) 의 복잡도를 지닌다고 합니다.
구현하는 법
구간 트리의 기본적인 구현의 원리는 이렇습니다. 주어진 구간을 반씩 쪼개어 트리 자료구조를 생성합니다. 더 이상 쪼갤 수 없게 되면, 요구되는 조건에 따라 최소값, 최대값, 또는 구간의 합을 차례로 채워나갑니다.
코드로 작성하게 되면 이런 모습이 됩니다. 아래의 코드는 객체로 구현한 최소값을 구하는 구간트리입니다
const createSegmentTree = (arr, start, end) => {
// 만약 시작점과 끝점이 같다면 해당하는 값을 리턴
// 재귀 함수로 구현했기 때문에 base case 에 해당
if (start === end) return { value: arr[start] }
// 시작점과 끝점이 같지 않다면 중간점을 찾아 2개의 구간으로 나누기
let middle = Math.floor((start + end) / 2);
// 편의상 왼쪽과 오른쪽으로 나누어 구간 분리
let left = createSegmentTree(arr, start, middle);
let right = createSegmentTree(arr, middle + 1, end);
// 현재 구간의 값을 value 에 넣고, 나뉜 구간을 각각 왼쪽과 오른쪽 노드로 나누어 할당
return {
value: Math.min(left.value, right.value),
left,
right
}
}
// 예시
const arr = [2, 5, 1, 4, 9, 3];
const tree = createSegmentTree(arr, 0, arr.length - 1);재귀 함수는 더 이상 작게 나누어지지 않을 때까지 쪼개어 base case 를 설정한 후, base case 를 기반으로 값을 쌓아올리게 되죠. 위에서 작성한 최소값을 구하는 구간트리의 코드도 마찬가지입니다. 시작점과 끝점이 같아지면 해당하는 값을 바로 리턴하게 되고, 그 값들을 기반으로 Math.min 메소드를 통해 트리를 역으로 쌓아올리게 됩니다.
출처: https://www.geeksforgeeks.org/segment-tree-set-1-range-minimum-query/
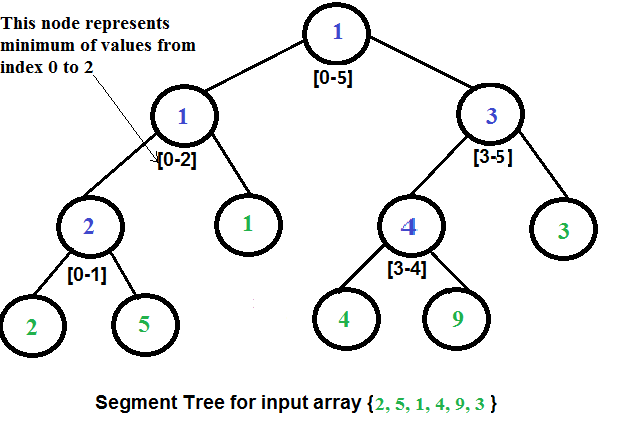
위의 이미지가 예시의 배열 [2, 5, 1, 4, 9, 3] 을 가지고 만든 구간트리의 모습입니다. (이미지에서는 자바스크립트가 아닌 다른 언어를 사용해서 배열을 중괄호로 표시하고 있습니다.)
노드의 제일 끝 점에 배열의 각 요소들이 값으로 들어가있습니다. 구간마다의 최소값은 역으로 트리의 가장 아래에서부터 채워지면서 올라가게 되죠.
원하는 구간을 찾는 법
구간 트리는 이진 트리의 형태로 구현할 수 있다는 것을 앞서 살펴보았습니다. 배열 [2, 5, 1, 4, 9, 3] 에서 0번째 요소부터 2번째 요소까지의 최소값은 위의 이미지에서 [0-2] 에 해당하는 노드에서 바로 찾을 수 있습니다.
하지만 만약 구간이 겹친다면 어떻게 찾아야 할까요? 찾고 싶은 구간이 2번째 요소에서부터 4번째 요소라면 말이죠. [2-4] 라는 노드는 구간 트리에는 없습니다. 노드가 없으니 값도 당연히 없겠죠.
대신 우리는 이렇게 생각해볼 수 있습니다. [2-4] 를 [2] 라는 구간과 [3-4] 라는 구간을 포함하는 구간으로 쪼개어보는 것이죠. [2] 라는 구간을 포함하는 노드와 [3-4] 라는 구간을 포함하는 노드는 이미 구간트리에 정리되어 있으니 이 둘을 비교해 최소값을 찾기만 하면 될 겁니다.
이를 코드로 표현하면 다음과 같습니다.
// rs 와 re 는 각각 구간의 시작점과 끝점
const findMinInTree = (start, end, rs, re, tree) => {
// 트리와 노드의 구간이 일치하거나 tree 가 구간 안에 포함되는 경우
if (rs <= start && end <= re) return tree.value;
// 구간과 트리가 겹치지 않는 경우
if (start < rs || end > re) return Number.MAX_SAFE_INTEGER;
// 겹치는 부분이 있는 경우
const middle = Math.floor((start + end) / 2);
return Math.min(findMinInTree(start, middle, rs, re, tree.left),
findMinInTree(middle + 1, end, rs, re, tree.right));
};위의 코드에서 핵심은 findMin 이라는 재귀 함수에 어떤 값들을 인자로 할당해주고 있는지입니다. start, end, middle 의 값은 앞서 구간 트리를 만들 때와 동일한 구조입니다. 이를 통해 각 노드의 구간 값을 재귀 함수에 할당하게 되는 셈이죠.
따라서 start, end 를 rs, re 와 비교하면 우리는 이미 정리된 구간 트리 노드를 위에서부터 차근차근 찾아나갈 수 있습니다. 만약 분할되어 있는 구간이 rs, re 의 범위 안에 있다면 더 이상 그 하위 레벨을 살펴보지 않고 재귀를 마칠 수 있죠.
위의 코드가 직관적으로 바로 이해되는 코드는 아닙니다. 하지만 개발자 도구에서 코드를 천천히 돌려가면서 해당하는 값들이 어떻게 변하는지를 살펴본다면 어느 순간 '아!' 하는 깨달음을 얻으실 수 있을 거라고 생각합니다. 저도 그랬었거든요. 귀한 시간을 내어 깨달음을 전해주신 코드스테이츠의 크루님에게 이 자리를 빌어 감사의 말씀을 전합니다. ㅎㅎㅎ
