"주말은 없다."
지난 한 주 간의 공부 중에서 다른 파트도 다 이해했다고 말할 수는 없겠지만, 자료 구조에 대한 공부는 특히나 이해하기 쉽지 않았습니다. 개념적인 설명 자체는 이해가 되는데 이것을 왜 사용하는지부터 또 어떻게 실제적인 활용으로 이어지는 지를 떠올리는 데까지는 아직 미치지 못하겠더라구요.
오늘은 트리 구조를 순회하는 3 가지 방법, 전위 순회, 중위 순회, 후위 순회을 소개하려고 합니다. 특히 개인적으로 위키백과에서 큰 깨달음을 얻었기 때문에 자료를 소개하고 제 나름의 설명을 덧붙일 예정이에요.
위키 백과의 트리 순회
트리 순회 라는 검색어로 구글링하면 위키백과의 자료가 뜨는데요. 보시면 트리 순회의 여러 분류들을 소개하고 있습니다. 저는 이 중 레벨 순서 순회 부분의 설명이 큰 도움이 되었습니다.
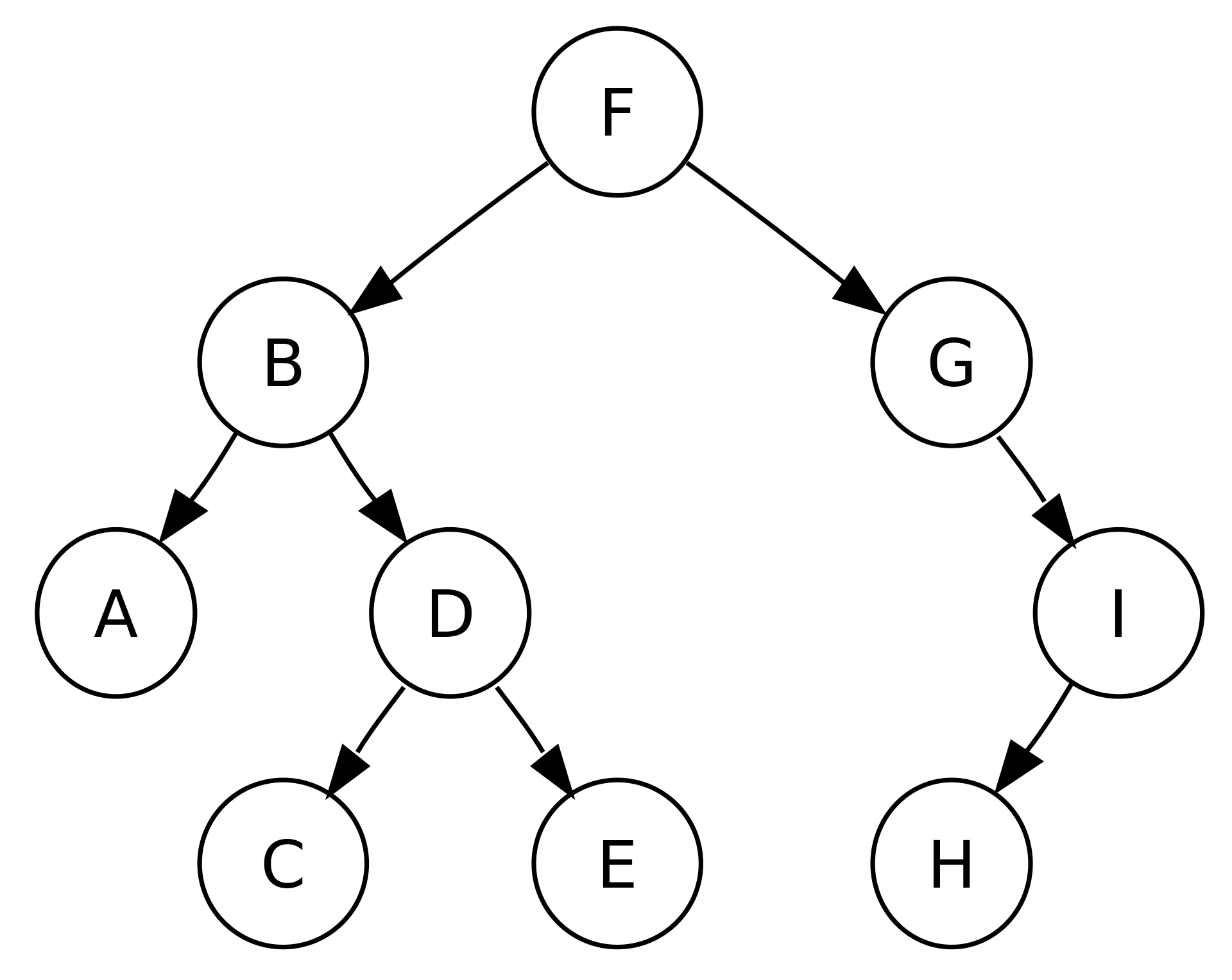
트리 구조 자료 출처: By Miles - 자작, 퍼블릭 도메인, https://commons.wikimedia.org/w/index.php?curid=1535668
이진 탐색 트리에서
전위 순회: F, B, A, D, C, E, G, I, H (root, left, right)
중위 순회: A, B, C, D, E, F, G, H, I (left, root, right)
후위 순회: A, C, E, D, B, H, I, G, F (left, right, root)
레벨 순서 순회: F, B, G, A, D, I, C, E, H
전위 순회
전위 순회는 상단의 인용 자료에서 볼드 처리한 것처럼 root, left, right 의 순서대로 진행하며 순회하기 시작합니다. 순회를 할 때 우선적으로 root 가 되는 나 자신을 먼저 체크하고 left, right 를 체크한다는 것이죠.
root 이후에 전위 순회는 left 에 Node 가 있는지를 파악합니다. left 에 Node 가 있다면 left 를 다시 root 로 해 순회를 반복하죠. 재귀를 적용할 수 있는 단서가 바로 여기에서 포착됩니다. left 를 먼저 탐색해 재귀를 적용하고 그 이후 right 에 재귀를 적용한다면, 위의 구조에서 전위 순회는 F, B, A, D, C, E, G, I, H 의 순서로 순회하게 되는 것이죠.
참고로 순회에 있어서 root 는 반드시 존재하는 값이라는 점을 기억해둘 필요가 있습니다. root 가 없다면 순회를 할 의미가 없겠죠. left 와 right 는 Node 가 있을 수도 없을 수도 있기에 구현할 때 조건을 넣어주어야 합니다.
중위 순회, 후위 순회
전위가 이해가 되신다면 중위 순회와 후위 순회는 금새 이해가 가능합니다. 중위 순회는 left, root, right 의 순서이고 후위 순회는 left, right, root 의 순서라는 것만 기억하면 되기 때문입니다.
앞에서 순회할 때 root 는 반드시 존재하는 값이라고 설명했습니다. 중위 순회는 left 부터 시작하기 때문에 left 에 Node 가 있는지부터 먼저 파악합니다. 그래서 시각적으로 가장 왼쪽에 위치한 A 라는 노드부터 방문하게 되는 것이죠.
A 에 도착하면 left 에 Node 가 없기 때문에 root 에서 자기 자신을 체크합니다. 그런 후에 right 를 체크하게 되는데, 여기에선 right 가 없으니 B 로 돌아가게 됩니다.
B 가 root 인 상황에서 left 의 모든 범위가 체크 완료되었으니 이제 자기 자신을 체크합니다. 그리고 right 에 Node 가 있는지를 파악하죠. D 라는 Node 가 있으니 right 로 넘어가 다시 중위 순회를 재귀적으로 불러오게 됩니다.
후위 순회도 마찬가지입니다. 후위 순회는 left 와 right 를 먼저 순회하기 때문에 root 가 가장 마지막에서야 체크됩니다.
전위 순회 = root, left, right;
중위 순회 = left, root, right;
후위 순회 = left, right, root;
라는 점을 숙지하고서 위의 트리 구조를 차근차근 복기해보시기를 추천합니다. 익숙해지셨다면 노트를 옆에 두고 순회 구조에 따른 Node 의 순서를 적어서 비교해보세요. 정확히 일치한다면 이제 우리도 3 종류의 트리 순회를 익숙하게 이해했다고 할 수 있습니다.
