- attention 기반의 encoder-decoder 알고리즘
- 순환신경망 기반이 아닌 attention 사용 (RNN 전혀 사용되지 않음)
- BERT, GPT, BART 등 다양한 application 존재
Attention
- 순환신경망 기반의 seq2seq 모델의 문제점을 보완하기 위해
- seq2seq 모델의 문제점 : 입력된 sequence data에 대해 하나의 고정된 벡터 정보(hidden state)만을 Decoder에 전달
- 이로 인해 입력된 모든 단어들의 정보가 제대로 전달되지 못한다는 문제 발생
- 입력된 단어가 많은 경우, 앞쪽에서 입력된 단어들의 정보는 거의 전달되지 못함
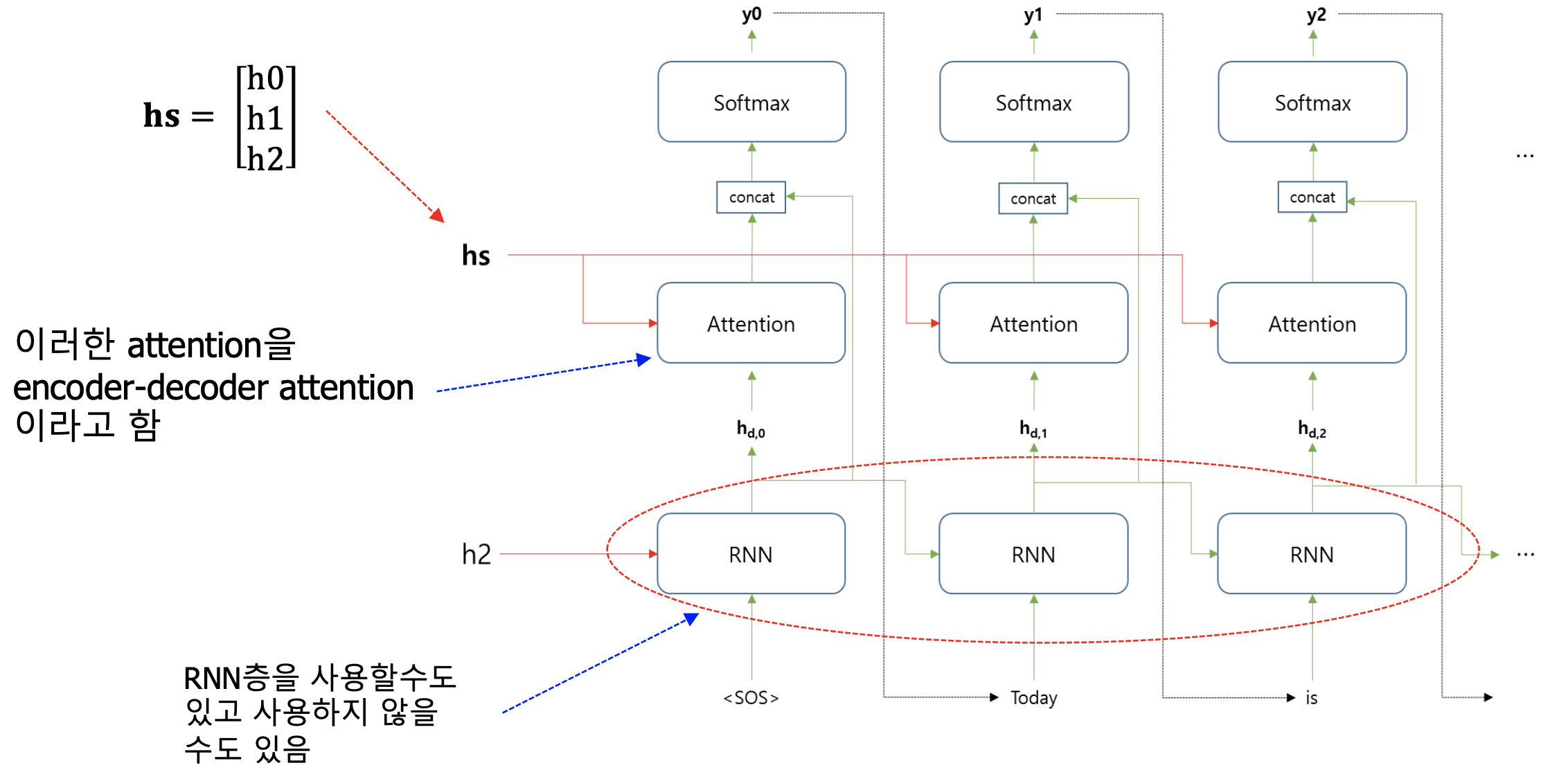
- 해결 위해 : Encoder 부분에서 각 단어에 대한 hidden state 정보를 모두 Decoder에 전달
- Decoder ; 언어 모델의 역할 수행 (이전 단어 정보를 이용하여 다음 단어 예측)
- Attention 기반의 Decoder : Encoder에서 전달된 모든 단어들의 hidden state 정보 사용
- 예측하고자 하는 단어와 관련이 더 많은 단어에 더 많은 attention 기울임
- attention 정도를 가중치로 표현
- Decoder ; 언어 모델의 역할 수행 (이전 단어 정보를 이용하여 다음 단어 예측)
- Encoder 출력 값 : 입력되는 단어들에 대한 hidden state 정보
- Decoder 역할 : Encoder에서 전달된 hidden state에 가중치 부여
-
Decoder 레이어에서 예측하고자 하는 단어와 더 많은 관련있는 Encoder 단어에 가중치를 더 크게
-
가중치 계산 예시 :
-
가중치 예시
-
attention 레이어에서 출력되는 값
→ 모든 입력 단어들에 대한 정보를 전달하고 (Encoder) 전달된 각 단어에 대해 예측해야 하는 단어와 가장 연관 있는 단어에 큰 가중치 부여 (Decoder)
-
- 가중치 계산 방식
- 각 입력 단어의 hidden state와 Decoder에서 예측하고자 하는 단어에 대한 hidden state의 유사도 가지고 계산
- hidden state 간 유사도 계산 ⇒ 내적 연산 : attention score
- attention score 값이 클수록 관련도가 크다는 것을 의미
- attention score를 가지고 가중치를 계산 → 확률값으로 표현됨
- 확률값 계산 : attention score에 softmax() 적용하여 계산
- 최종 출력 값
- attention에서 출력되는 값과 각 레이어에서 출력되는 값들을 concat
- Attention을 이용한 decoder 구조
Self - Attention
- Attention과의 차이
- Attention : encoder-decoder 모형에서 encoder에서 decoder로 넘어가는 정보에 가중치를 주는 방식으로 작동
- Self-Attention : 입력된 텍스트 데이터 내에 존재하는 단어들 사이의 관계를 파악하기 위해 사용
- 지시대명사가 무엇을 의미하는지 등을 파악하는 데에 유용함
- 입력된 데이터 내에 존재하는 다른 단어들과의 관계를 파악할 수 있도록 가중치 부여
- encoder - decoder attention과의 차이 : hidden state가 아니라 embedding vector를 사용해 내적 연산 진행
- 예시
- 각 단어에 대한 embedding vector
- 에 대한 attention score
- attention score 계산 : 에 대한 embedding vector와 다른 단어들의 embedding vector와의 내적 연산
- 가중치 계산
→ 가중치의 값 계산 : Attention score를 softmax()를 적용하여 계산
- embedding vector와 가중치 곱
- self-attention 결과 도출
- 각 단어에 대한 embedding vector
- Transformer에서의 self-attention
- 입력 받은 단어들 중 어떠한 단어에 더 많은 가중치를 주어야하는지 파악하기 위함
- 각 단어들에 대한 Query, Key, Value의 서로 다른 3가지 벡터 사용 : 임베딩 벡터에서 K, Q, V 도출
- Key : 단어의 id와 같은 역할
- Value : 해당 단어에 대한 구체적 정보를 저장하는 역할
- Query : 유사한 다른 단어를 찾을 때 사용되는 질의 벡터
- 작동 순서
1) 입력된 각 단어들에 대해 Query, Key, Value 벡터 계산 (각각의 가중치 행렬 사용됨)
2) Attention Score 계산 : 특정 단어의 Query 벡터와 각 단어들에 대한 Key 벡터의 내적 연산
3) Attention Score 이용하여 가중치 계산 : Softmax() 함수 사용
4) 가중치를 Value 벡터에 곱하기 (embedding 벡터에 곱하는 것이 아님)
5) 최종 결과 도출 : 가중치가 곱해진 Value Vector들의 합
- Query, Key, Value 벡터 구하기
- 별도의 가중치 행렬 사용
- 입력된 각 단어의 임베딩 벡터와 가중치 행렬의 곱을 통해 Q, K, V 벡터 구함 ex) Query 가중치와 입력 단어 임베딩 벡터를 곱해서 각 입력 단어에 대한 Query 벡터 구하기
- 수식으로 표현
: Query 벡터들에 대한 행렬
K$ : Key 벡터들에 대한 행렬
: Value 벡터들에 대한 행렬
와 의 곱 : Query 벡터들과 Key 벡터들의 내적 연산 의미 - 각 행별로 각 단어에 대한 attention score를 의미함
Transformer
-
Attention 기반의 encoder-decoder 모형
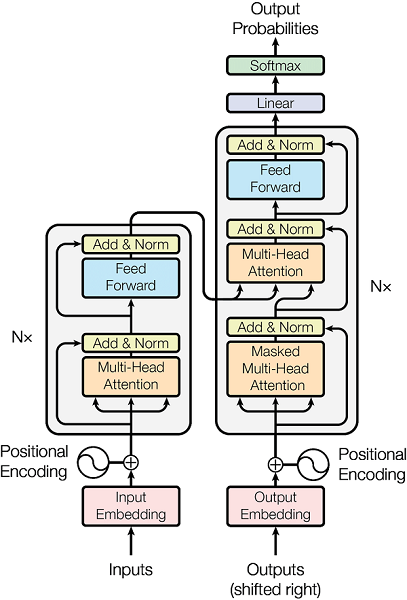
- Encoder block과 Decoder block을 여러개 쌓아서 encoder 부분과 decoder 부분을 생성
-
Encoder 부분
-
Encoder block 6개 사용
-
Multi-Head Attention : 입력된 sequence data에 대해 Self-Attention 여러개 적용
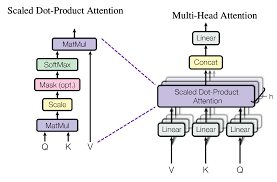
- Scaled dot-product attention
- : Key Vector의 크기 - Multi-head attention
- where
- Q, K, V를 바로 사용하지 않고 linear projection을 한번 더 진행
- Transformer의 경우 : h = 8
- 사용 이유
1) 주목해야 하는 다른 단어가 무엇인지를 더 잘 파악
2) 각 단어가 갖고 있는 특성을 더 잘 표현
- Scaled dot-product attention
-
Add & Norm layer
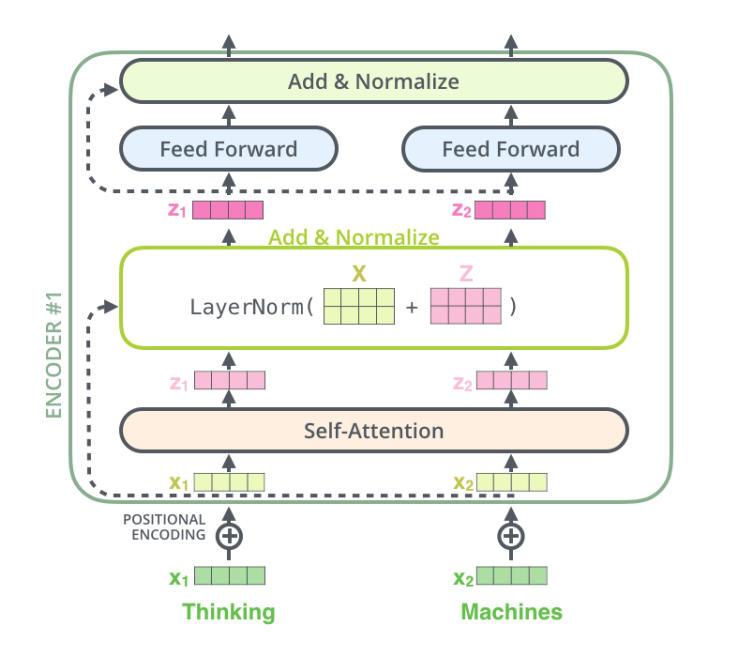
- self-attention 레이어가 출력하는 값과 각 단어들의 임베딩 정보를 더해서 layer normalization이 수행됨
- Layer Normalization : 각 관측치에 대해 하나의 레이어에 존재하는 노드들의 입력값들의 정보를 이용해 표준화하는 것을 의미 (입력값 사이에 큰 차이가 나는 것을 막고자)
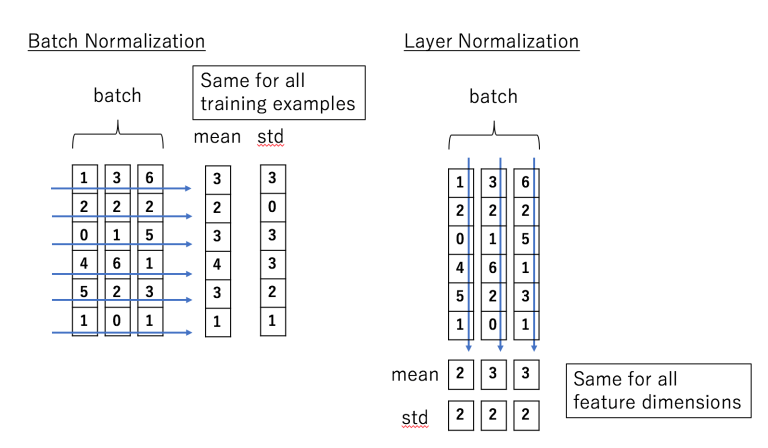
- Layer Normalization : 각 관측치에 대해 하나의 레이어에 존재하는 노드들의 입력값들의 정보를 이용해 표준화하는 것을 의미 (입력값 사이에 큰 차이가 나는 것을 막고자)
- self-attention 레이어가 출력하는 값과 각 단어들의 임베딩 정보를 더해서 layer normalization이 수행됨
-
Position-wise feed-forward network
- 2개의 fully connected layer로 구성됨
- Token(Position)마다 독립적으로 적용
- 첫번째 Layer에 ReLU 활성화함수 사용
- : 첫번째 FCL에 입력되는 입력 벡터
- : 입력 벡터와 첫번째 FCL 사이의 가중치 행렬
- : 첫번째 FCL과 두번째 FCL 사이의 가중치 행렬
-
위치정보 임베딩 (Positional Embedding)
- Transformer 모형에서는 단어들의 embedding정보와 더불어 입력된 시퀀스 데이터 내에서의 위치 정보 또한 사용
- 위치 정보 사용시, 단어들 간의 상대적인 거리 파악
- 순환신경망 구조를 사용하지 않고 attention 방법을 사용하기 때문에 Positional Embedding을 사용함
- 단어들이 갖는 상대적인 위치 정보를 반영하기 위해 위치 정보를 반영하는 positional embedding 벡터 사용
- Transformer 모형에서는 단어들의 embedding정보와 더불어 입력된 시퀀스 데이터 내에서의 위치 정보 또한 사용
-
-
Decoder 부분
- seq2seq의 decoder와 비슷하게 작동함
- 언어 모형으로 생각 가능
- 두가지 종류의 attention 사용
- Masked self-attention
- Encoder-Decoder attention
- Key, Value 벡터는 Encoder에서 전달됨
- Query 벡터는 Decoder의 입력값을 사용해서 전달
→입력된 단어에 대해서 masked self-attention layer와 add&norm layer를 거쳐 전달되는 값
-
Encoder-Decoder attention
- Self-attention과 마찬가지로 query, key, value 벡터들을 사용
- query 벡터 : decoder 부분에 현재 단계에 입력된 단어에 대한 query 벡터
- key, value 벡터 : encoder 부분에서 (encoder 부분에 입력된) 각 단어에 대한 값으로 전달
- 작동방식은 self-attention과 동일
- Self-attention과 마찬가지로 query, key, value 벡터들을 사용
-
Masked self-attention
- 현재 decoder 부분에 입력된 단어의 이전 단어들에 대해서만 계산 진행
- decoder가 언어모형으로 사용되기 때문 (현재 단어까지의 정보만을 가지고 다음 단어들은 아직 예측되지 않아 어떠한 단어가 올지 모르기 때문)
- 현재 입력된 단어를 기준으로 그 다음 단어들에 대해서는 신경쓰지 않음
- attention score를 구한 뒤 현재 단어 다음 단어들에 대해 attention score 값으로 대체함 → 를 적용하면 해당 값은 0으로 변환
- 현재 decoder 부분에 입력된 단어의 이전 단어들에 대해서만 계산 진행
-
Transformer 응용 예시
- BERT (Bidirectional Encoder Representations from Transformers)
- Transformer의 encoder 부분만을 사용함
- 문서/단어 임베딩, 문서 분류, Q&A, 단어들 간의 관계 추출
- GPT (Generative Pre-trained Transformer)
- Transformer의 decoder 부분만을 사용
- 텍스트 생성
- BART (Bidirectional and Auto-Regressive Transformers)
- Transformer의 encoder와 decoder 모두 사용
- 텍스트 요약
- BERT (Bidirectional Encoder Representations from Transformers)
