[백준]15989 1, 2, 3 더하기 4

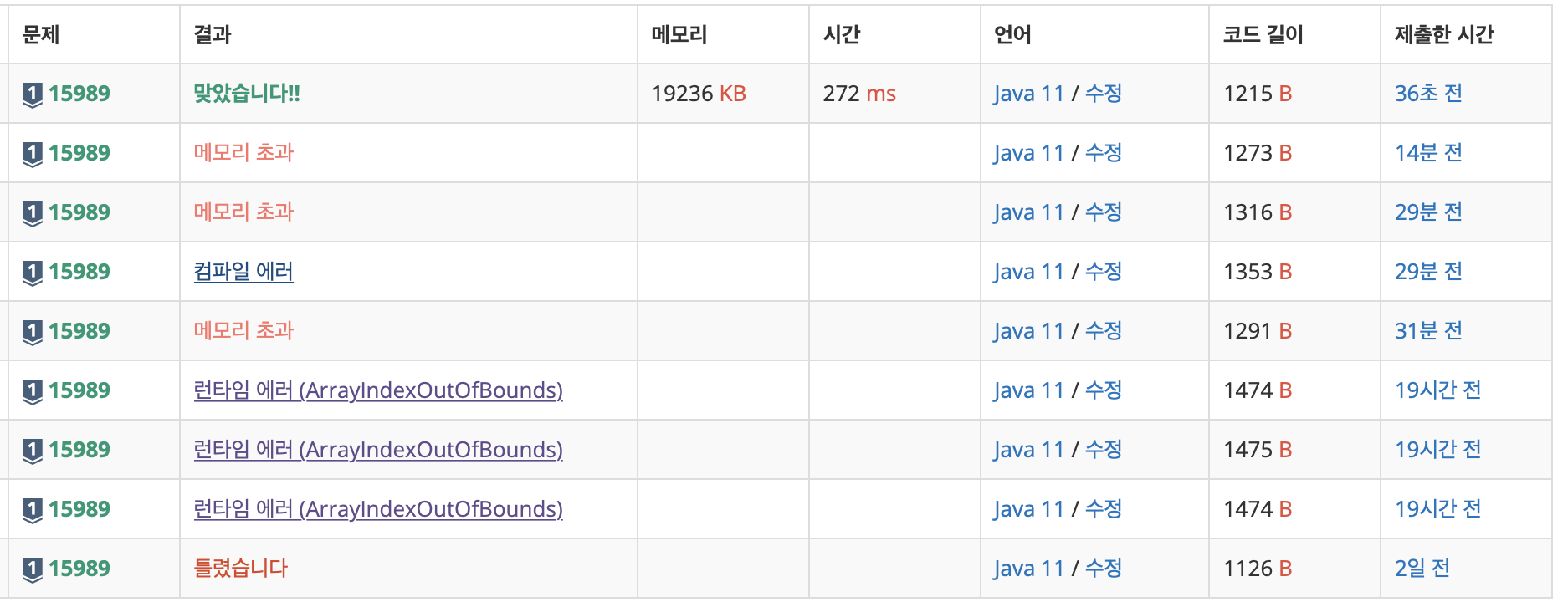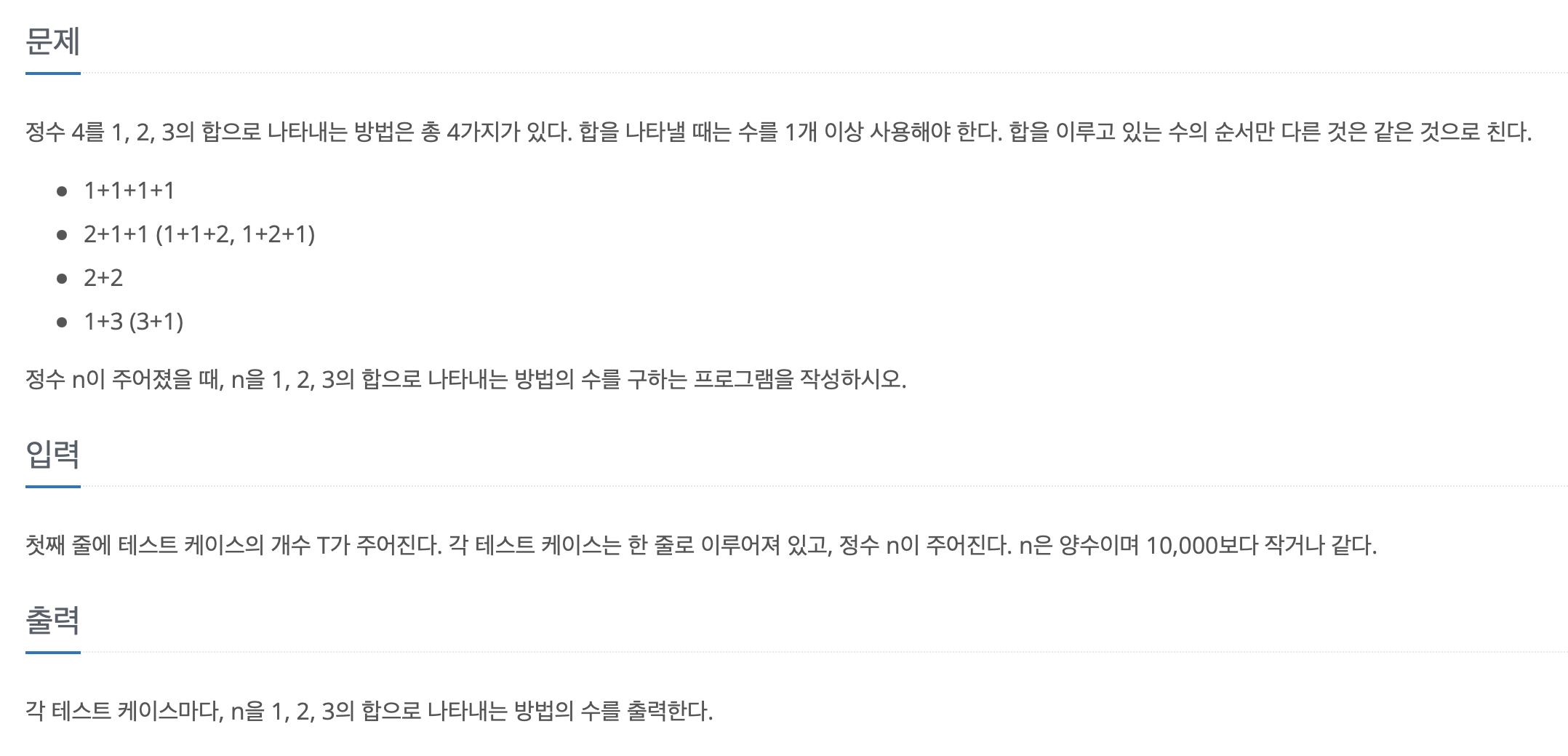
1, 2, 3 더하기 풀었어서 좀만 생각하면 풀 수 있을 줄 알았는데 장렬히 패배했다. 이차원 배열까진 생각도 못했는데.. 풀이도 읽고 또 읽어서 겨우 이해했다ㅠ 내겐 너무 먼 dp 🥲

package baekjoon;

import java.util.Scanner;

public class Main_15989 {
    public static void main(String[] args) {
        // 각 테스트 케이스마다 n을 1,2,3의 합으로 나타내는 방법의 수를 출력한다
        // 합을 이루고 있는 수의 순서만 다른 것은 같은 것으로 친다
        Scanner sc = new Scanner(System.in);
        StringBuffer sb = new StringBuffer();
        int T = sc.nextInt();
        int[] result = new int[T];
        int[][] dp = new int[10001][4];

        dp[1][1] = 1;
        dp[1][2] = 0;
        dp[1][3] = 0;

        dp[2][1] = 1;
        dp[2][2] = 1;
        dp[2][3] = 0;

        dp[3][1] = 1;
        dp[3][2] = 1;
        dp[3][3] = 1;

        for (int i = 4; i <= 10000; i++) {
            dp[i][1] = dp[i-1][1];
            dp[i][2] = dp[i-2][1] + dp[i-2][2];
            dp[i][3] = dp[i-3][1] +dp[i-3][2]+dp[i-3][3];
        }

        for (int i = 0; i < T; i++) {
            int n = sc.nextInt();
            sb.append(dp[n][1] + dp[n][2] + dp[n][3]+"\n");
        }
        System.out.println(sb);
    }
}

👩‍💻 풀이
기존 문제와 동일했지만 달라진 점이 있다면 중복을 허용하지 않는 것! 직전에 구해둔 값에 +1로 만들 수 있는 경우 / +2로 만들 수 있는 경우 / +3으로 만들 수 있는 경우를 통해 점화식에 접근하는 것까진 같았지만 1,2 = 2,1 이런 중복을 막아야해서 아주 골머리를 싸맸다.

이해하는데도 오래걸렸던 이번 문제..
이차원 배열로 1을 더해 만들 수 있는 조합, 2를 더해 만들 수 있는 조합, 3을 더해 만들 수 있는 조합을 각자 저장해두어야 한다.

예를들어
4를 만들 수 있는 조합은
1 1 1 +1
1 2 +1
3 +1

1 1 +2
2 +2

1 + 3

이렇게 dp[n-1] + dp[n-2] + dp[n-3] 인데 여기서 1 2 + 1 과 1 1 +2 의 중복이 발생한다. 중복방지를 위해 1로 끝나면 dp[4][1] 에 담고 2로 끝나면 dp[4][2]에 담고 3으로 끝나면 dp[4][3] 에 담도록 한다. 여기서 중요한 포인트는 중복제거를 위해 무조건 오름차순으로 체크해야 한다는 것.

그럼
3에서 만들 수 있는 4는
1 1 1 1
1 1 2
1 3

1 1 2
2 2

1 3

이렇게 되는데
1로 끝나는 수는 dp[4][1] = dp[3][1] 이 된다. 1 1 2와 1 3 은 1로 끝나지 않으니까!
2로 끝나는 수는 dp[4][2] = dp[2][1] + dp[2][2] 가 된다. 2를 만드는 조합에 +2
3으로 끝나는 수는 dp[4][3] = dp[1][1] + dp[1][2] + dp[1][3]

이해하는데 한참 걸렸다 사실 쓰면서도 긴가민가하는데 계속계속 봐야겠다..😭 글로 쓰면서도 모르겠네..