[완전탐색] 소수찾기

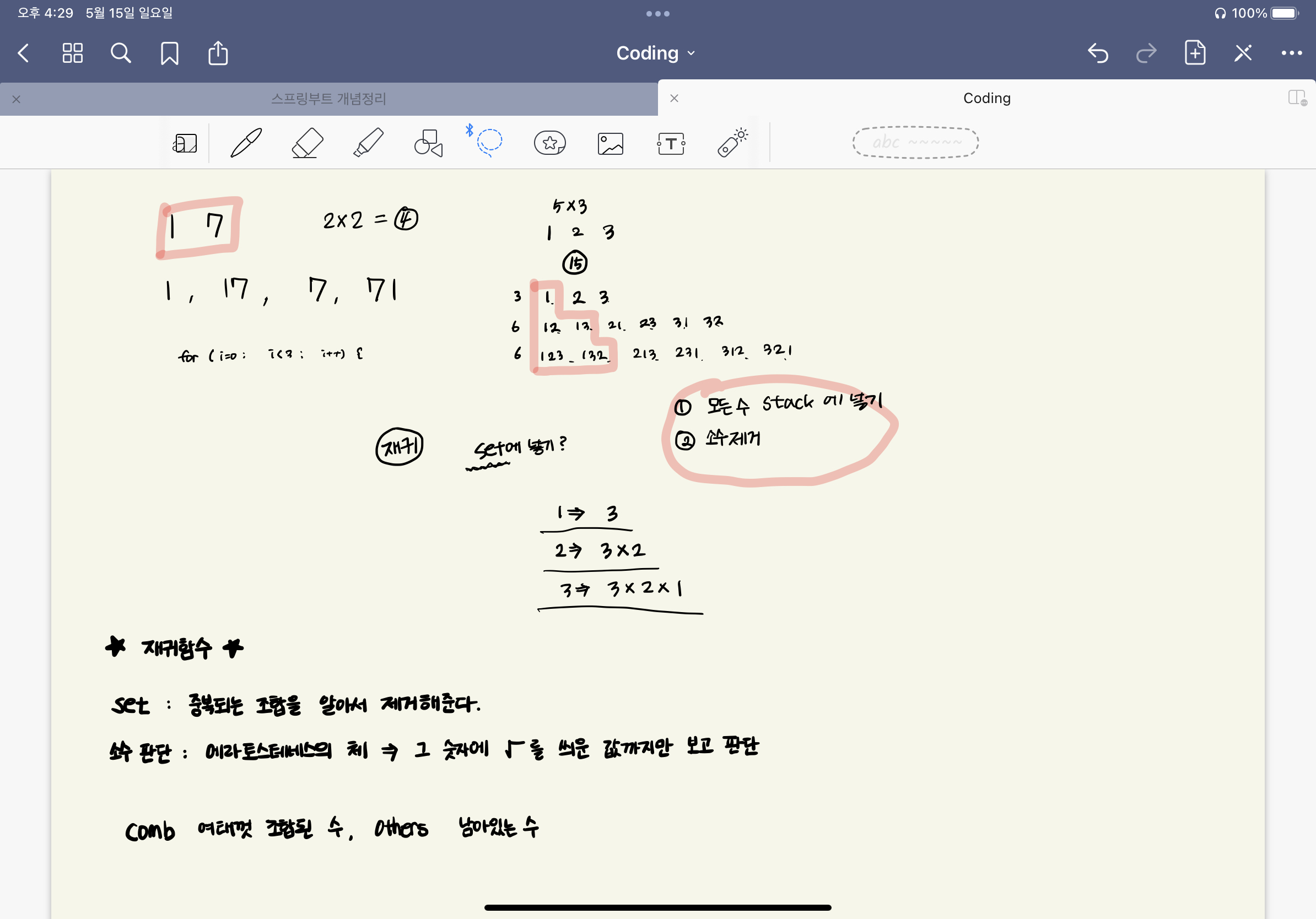
HashSet<Integer> hs = new HashSet<>();

public int solution(String numbers) {
        int answer = 0;

        // 모든 조합 구하기
        recursive("", numbers);

        // 소수 갯수 세기
        Iterator<Integer> it = hs.iterator();
        while(it.hasNext()) {
            int number = it.next();
            if(isPrime(number)) {
                answer++;
            }
        }

        // 소수 갯수 반환
        return answer;
    }

    public boolean isPrime(int num) {
        // 0과 1은 소수 X
        if (num == 0 || num == 1) {
            return false;
        }

        // 에라토스테네스의 체의 limit을 계산 (루트를 씌운 값)
        int limit = (int) Math.sqrt(num);

        // limit 까지만 배수여부 확인
        for (int i = 2; i <= limit; i++) {
            if (num % i == 0) {
                return false;
            }
        }

        return true;
    }
    
    /*
        comb : 여태껏 조합된 수
        others : 남아있는 수
     */
    public void recursive(String comb, String others) {

        // 현재 조합 저장
        if (!comb.equals("")) {
            System.out.println(comb);
            hs.add(Integer.valueOf(comb));
        }

        for (int i = 0; i < others.length(); i++) {
            // 현재 조합+현재 숫자 , 현재 숫자를 뺀 나머지 숫자를 파라미터로 전달
            recursive(comb + others.charAt(i), others.substring(0, i) + others.substring(i + 1));
        }
    }

풀어보려고 매우 끙끙댔으나 결국 다른 사람 풀이를 보고 이해했다
이 문제는 재귀함수가 핵심 키워드였다
중복되는 조합을 알아서 제거해주는 HashSet에 조합들을 저장했고 재귀함수를 통해 현재 선택된 숫자에서 있을 수 있는 모든 경우의 수를 구했다
소수 판단은 에라토스테네스의 체로 소수인지 알고 싶은 숫자에 루트를 씌운 값까지만 보고 판별하였다
소스는 매우 간단한데 이해하기까지 시간이 조금 걸렸다 재귀함수 관련 문제는 많이 풀어봐야 알 것 같다