[자료구조 및 알고리즘] Algorithm Analysis

신동욱·2024년 12월 17일

목록 보기

1/18

알고리즘 분석이란 무엇인지, 알고리즘을 이야기할 때 많이 등장하는 빅-오 표기법이 뭔지 알아보겠습니다! 🔍✨

1. Algorithm Analysis 🚀

알고리즘(Algorithm)은 문제를 해결하기 위한 절차입니다. 1부터 10까지의 합을 구하는 동일한 역할의 두 개의 프로그램 중 어느 것이 더 나은 프로그램일까요?

위의 두 함수를 비교해 보면 sum_of_n() 함수가 foo() 함수보다 가독성이 더 좋기 때문에, 더 좋다고 할 수 있습니다. 그러나, 컴퓨팅 자원(Computing Resource)의 관점에서 보면 두 함수는 동일한 알고리즘을 기반으로 구현되었습니다.

💡 컴퓨팅 자원

Algorithm Analysis에서 관심을 갖는 것이 바로 컴퓨팅 자원의 관점에서 비교하는 것입니다. 컴퓨팅 자원이란 크게 두 가지로 나뉩니다.

공간 (Space) :
- 알고리즘이 문제를 해결하기 위해 사용하는 메모리 양입니다.
- 이는 알고리즘을 실행하는 데 필요한 모든 변수들을 고려하거나, 운영체제(OS)의 메모리 소비 측정을 통해 평가할 수 있습니다.
시간 (Time)
- 알고리즘이 문제를 해결하는 데 걸리는 실행 시간입니다.
- 이는 time() 함수나 프로파일러(profiler)를 사용하여 측정할 수 있습니다.

🔧 실행 시간 측정 : 벤치마크 분석

다음 코드는 벤치마크 분석을 통해 프로그램 실행 시간을 측정하는 방법을 보여줍니다.

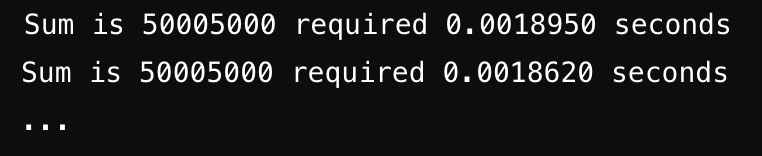
⚡️ 알고리즘에 따른 실행시간 차이

위 예시처럼 1부터 N까지의 합을 구하는 함수를 더 빠르게 할 수 있을까요? 1부터 N까지의 합은 공식이 존재해, 앞선 예시처럼 반복문을 돌 필요는 없습니다. 수학식을 이용하는 방법의 소요 시간은 아래와 같습니다.

같은 문제를 해결하는 두 프로그램의 비교를 통해, 연산을 반복하는 것은 더 많은 시간을 소요한다는 것을 알 수 있습니다.

2. Big-O 표기법 📐

직접 실행 시간을 측정하는 벤치마크 분석은 특정 환경(컴퓨터, 언어, 컴파일러 등)에 의존적이므로 한계가 있습니다. 알고리즘의 효율성을 환경에 독립적으로 평가하기 위해 Big-O 표기법을 사용합니다.

문제 크기와 실행 시간 관계 : T(n) 📊

앞서 살펴본 것처럼, 수식이 많이 반복되면 시간이 오래 걸린다는 것을 알았습니다. 그렇다면 Algorithm Analysis를 위해 수식의 개수를 세는 방법이 유효할 수 있습니다. 더욱 간소화하여, 할당문(assignment statements)의 수를 세보도록 합시다.

def sum_of_n(n):
	the_sum = 0					# 할당
    for i in range(1, n+1):
    	the_sum = the_sum + i	# 할당
    return the_sum

print(sum_of_n(10))

함수 sum_of_n에서 할당문의 수는 the_sum = 0의 1번과 the_sum = the_sum + i가 실행되는 n번을 합한 값입니다. 이를 함수 $T(n)$ 로 나타낼 수 있으며, $T(n)=1+n$ 입니다.

여기서 매개변수 n은 "문제의 크기"라고 불리며, $T(n)$ 은 크기가 n인 문제를 해결하는데 걸리는 시간, 즉 $1+n$ 단계가 필요함을 나타냅니다.

🎲 예시

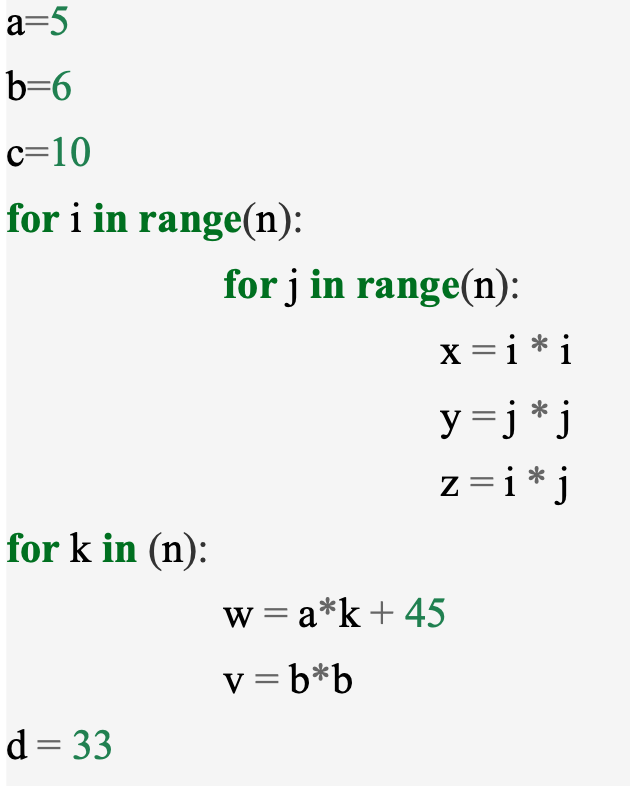
위 예시에서 $T(n)=3+3n^2+2n+1$ 입니다.

🏆 지배적인 항

그런데 연산의 정확한 개수보다는 $T(n)$ 함수에서 가장 지배적인 부분을 찾는 것이 더 중요하다는 것이 알려져 있습니다. 즉, 문제의 크기 n이 커질수록 $T(n)$ 함수의 일부가 나머지를 압도합니다. 이 지배적인 항이 결국 알고리즘을 비교할 때 사용됩니다. 이를 Big-O 표기법으로 나타내며, 이는 $O(f(n))$ 형태로 쓰입니다.

Big-O 표기법은 계산에서 실제 연산 단계 수를 간단히 근사화하여 나타냅니다. 함수 $f(n)$ 은 원래 $T(n)$ 함수의 지배적인 부분을 간단히 표현한 것입니다.

예시 1: $T(n) = 1 + n$

위의 예제에서 $T(n) = 1 + n$ 입니다. $n$ 이 커질수록 상수 $1$ 의 영향은 점점 줄어듭니다. 따라서 $T(n)$ 을 근사화할 때 상수 $1$ 을 무시하고 실행 시간을 $O(n)$ 으로 표현할 수 있습니다. 여기서 $1$ 은 $T(n)$ 에 영향을 주지만, $n$ 이 커지면 근사치에 거의 영향을 미치지 않게 됩니다.

에시 2: $T(n) = 5n^2+27n + 1005$

$n$ 이 작을 때(1 or 2..)는 상수 $1005$ 가 가장 큰 영향을 미칩니다. 그러나 $n$ 이 커지면 $n^2$ 항이 가장 중요한 역할을 하게 됩니다. 실제로, $n$ 이 매우 클 경우 다른 두 항은 최종 결과에 거의 영향을 미치지 않습니다. 따라서 이 $T(n)$ 함수는 $O(n^2)$ 로 표현합니다.

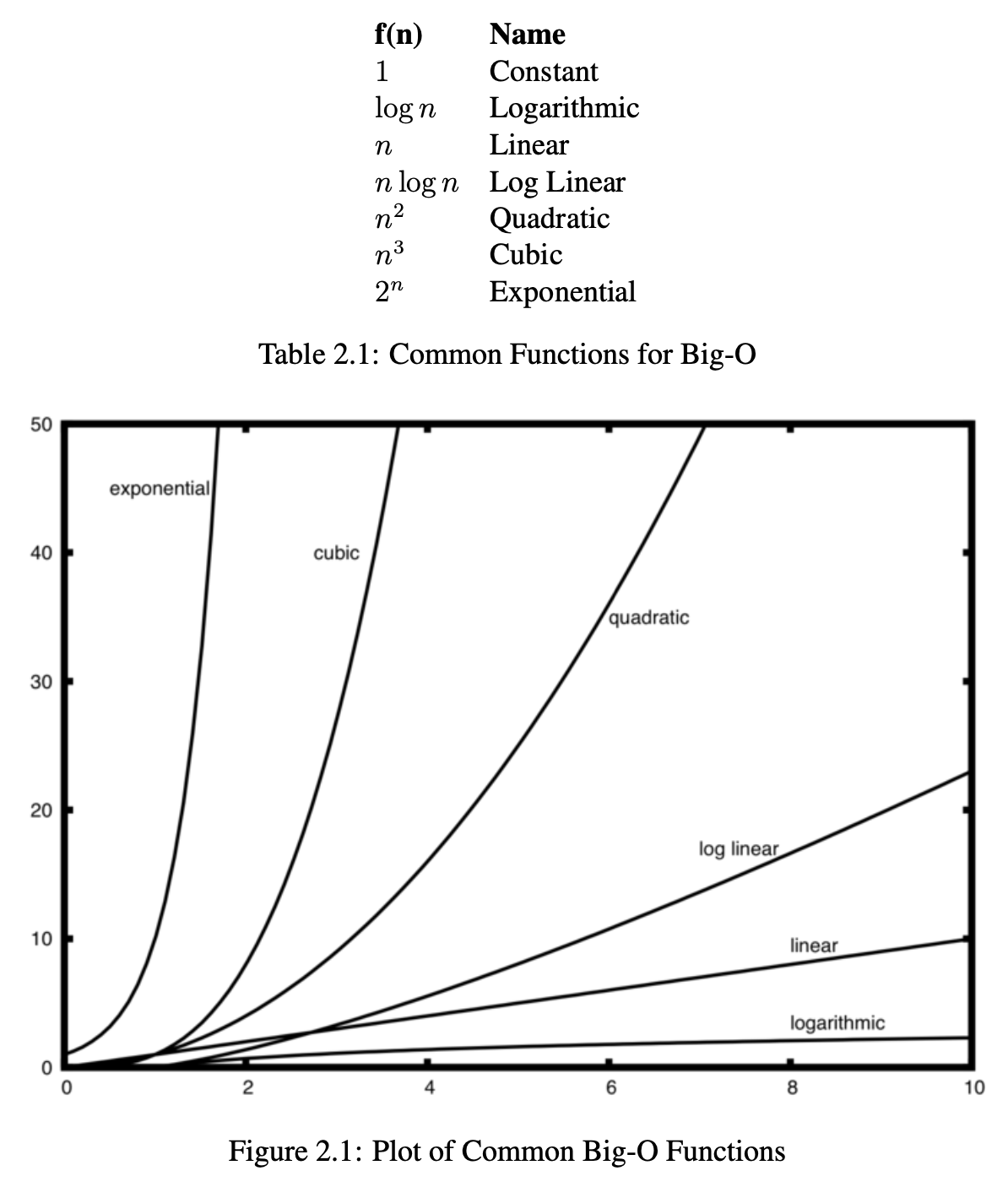
위 그림은 여러 f(n)의 형태에 따라 시간복잡도가 어떻게 변하는지 잘 나타내고 있습니다.

😱 최악의 경우(Worst Case)

Big-O 표기법은 점근적 상한으로 정의됩니다. 이는 입력 크기 n가 매우 커질 때, 알고리즘의 실행 시간이 어떻게 증가하는지 상한을 기준으로 나타낸 것입니다.

일반적으로 최악의 경우(worst case)를 기준으로 Big-O를 계산하기 때문에, 최악의 경우를 이해하면 Big-O 표기법을 쉽게 이해할 수 있습니다.

🔍 예제 : 배열에서 선형 탐색으로 문자 'a' 찾기

경우	비교 횟수	Big-O	설명
Best	1	O(1)	첫 원소에서 ‘a’ 발견
Average	n/2	O(n)	무작위 배치 → 절반쯤에서 발견
Worst	n	O(n)	마지막 위치에서 발견 or 없음

best case : {'a', 'b', 'c'} -> 딱 한 번의 비교
worst case : {'c', 'b', 'a'} -> n번 비교
average case : 입력 배열의 요소가 랜덤하게 배치되어 있다면, 평균적으로 배열의 중간까지 탐색한 후에 결과를 찾습니다. 이는 대략 $n/2$ 번의 비교를 필요로 하며, Big-O 표기법으로는 역시 $O(n)$ 로 표현됩니다.

3. Example : Anagram Detection 🧩

애너그램(Anagram)이 뭔? 🔄

애너그램은 문자열 재배열 문제를 의미합니다. 한 단어 또는 문장의 문자를 재배열하여 다른 단어 또는 문장을 만드는 것을 말합니다.

에시

"heart" -> "earth" (애너그램)
"listen" -> "silent" (애너그램)
"python" -> "typhon" (애너그램)
"hello" -> "world" (애너그램 아님)

방법1 : Brute Force 💥

두 단어가 애너그램 관계인지 알기 위해, 모든 재배열을 구한 후 비교하는 방법을 생각해볼 수 있습니다.

Step 1 : 모든 가능한 재배열을 만든다.
	'mary' -> 'mary', 'mayr', 'mray', ....
Step 2 : 'army'와 비교한다

Step1에 대해서는 $O(n!)$ 로 표현할 수 있습니다.
Step2에 대해서 최악의 경우 문자열의 길이만큼 비교하므로, $O(n)$ 입니다.

따라서, 이 방법은 $O(n!)$ 입니다.

방법2 : Checking Off ✅

두 문자열을 순회하면서, 같은 문자가 있으면 해당 문자를 제거하는 방식으로 애너그램 관계를 확인할 수 있습니다.

def anagram_solution(s1, s2):
	a_list = list(s2);
    
    pos1 = 0
    still_ok = True
    
    while pos1 < len(s1) and still_ok:
    	pos2 = 0
        found = False
        while pos2 < len(a_list) and not found:
        	if s1[pos1] == a_list[pos2]:
            	found = True
            else:
            	pos2 = pos2 + 1
        if found:
        	a_list[pos2] = None
        else:
        	still_ok = False
        
        pos1 = pos1 + 1;
        
    return still_ok

print(anagram_solution('abcd', 'dcba')

위 알고리즘의 worst case는 'abcd'와 'bcda'처럼 문자열의 순서가 반대인 경우입니다. 4번, 3번, 2번, 1번의 순서로 연산이 이루어지고 있습니다. $1 + 2 + 3 + ... + n$ 와 동일한 알고리즘입니다.

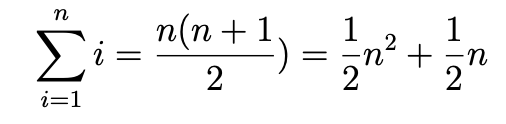
따라서, 이 방법은 $O(n^2)$ 입니다.

방법3 : Sort and Compare 🔃

두 단어가 애너그램 관계에 있다면, 정렬을 수행했을 때 동일한 문자열로 바뀌어야 합니다.

Step 1 : 각 단어를 정렬한다.
	Sort('mary') -> 'army'
    Sort('army') -> 'army'
Step 2 : 같은 위치의 문자를 비교한다.

정렬 알고리즘은 $O(n logn)$ 으로 알려져 있습니다.
또 Step2에서 길이가 n인 문자열을 두 번 순회하므로 $O(n)$ 입니다.

따라서, 이 방법은 $O(nlogn)$ 입니다.

방법4 : Count and Compare 📊

두 단어가 애너그램 관계에 있다면 사용된 각각의 알파벳 개수가 동일해야 합니다. 이 사실을 이용하면, $O(n)$ 으로 문제를 해결할 수 있습니다.

각 알파벳과 대응하는 길이가 26인 count 배열을 선언합니다. 그리고 두 단어를 순회하면서 대응되는 알파벳의 개수를 기록해 놓습니다. 이제 길이가 26인 배열을 순회하면서, 개수가 같은지 비교합니다.

Step 1 : 문자의 개수를 셉니다.
	count_mary = [1, 0, 0, ..., 1, 0, ..., 1, 0, ..., 1, 0]
    count_army = [1, 0, 0, ..., 1, 0, ..., 1, 0, ..., 1, 0]
    
Step 2 : 두 count 배열의 비교

Step1은 $T(n) = 2n$ 이므로 $O(n)$ 입니다.
Step2는 $T(n) = 26$ 으로 $O(1)$ 입니다.

따라서, 이 방법은 $O(n)$ 입니다. 하지만, 다른 방법에 비해 메모리를 많이 사용하였습니다. 💾

마무리 🎉

알고리즘 분석(Algorithm Analysis)과 빅오 표기법(Big-O Notation)은 효율적인 코드를 설계하고 평가하는 데 중요한 도구입니다.

알고리즘의 성능을 평가할 때는 시간(Time)과 공간(Space)이라는 두 가지 컴퓨팅 자원을 고려합니다. 이를 정량적으로 비교하기 위해, 특정 환경(예: 컴퓨터 성능이나 프로그래밍 언어 등)에 의존하지 않는 Big-O 표기법을 사용합니다.

Big-O 표기법은 문제 크기 n이 증가할 때 알고리즘의 실행 시간을 단순화하여 나타냅니다. 이 과정에서 지배적인 항만을 고려하여 복잡도를 평가하며, 일반적으로 최악의 경우(worst case)를 기준으로 분석합니다.

애너그램(Anagram) 문제를 통해 Big-O 표기법을 실습하고, 같은 문제를 해결하는 여러가지 알고리즘을 학습하였습니다. 🧠✨

참고 📚

https://www.cs.auckland.ac.nz/courses/compsci105ssc/resources/ProblemSolvingwithAlgorithmsandDataStructures.pdf

신동욱

다음 포스트

[자료구조 및 알고리즘] Algorithm Analysis