BFS와 DFS

📃 그래프 탐색에서 사용되는 BFS와 DFS 알고리즘에 대해 공부하며 정리한 글입니다.

그래프란?

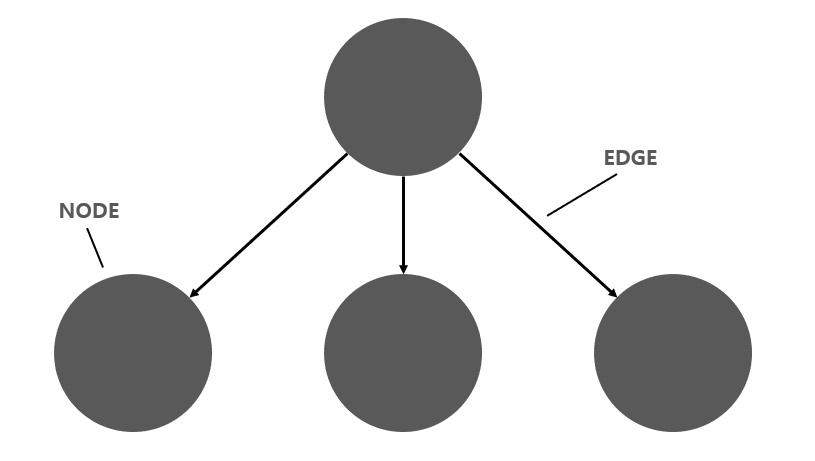
간선(Edge)로 연결되어 있는 각 정점(Node)들의 구조를 말한다.

그래프 탐색?

어떤 한 그래프와 해당 그래프의 시작 노드가 주어졌을 때, 시작 점에서 간선을 타고 이동할 수 있는 모든 노드들을 탐색하는 문제를 의미한다.

이 때 그래프 탐색 문제를 해결하기 위해 BFS와 DFS를 이용할 수 있다.

---

BFS

* 너비 우선 탐색 ( Breadth-First Search )

BFS는 너비 우선 탐색으로 불리며 이름에 맞게 그래프의 시작점에서 너비가 가까운 노드를 우선적으로 탐색한다.

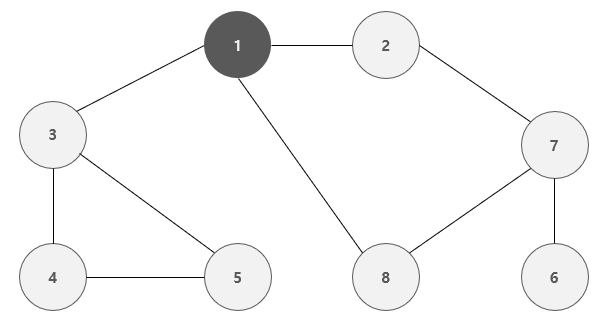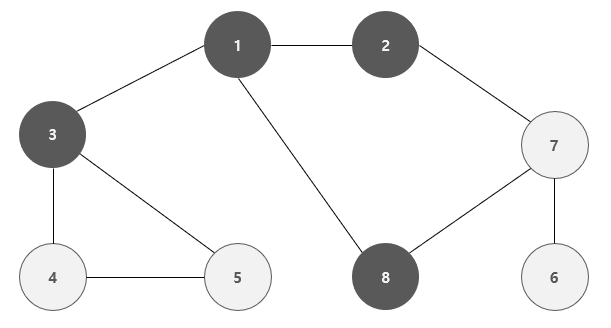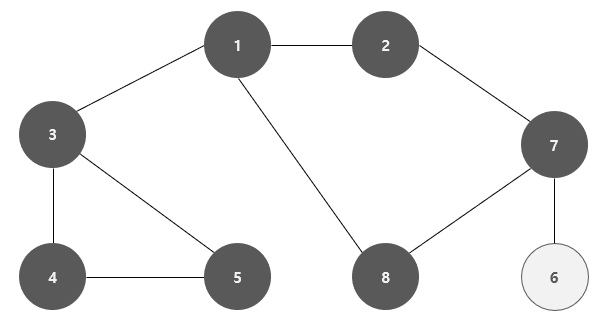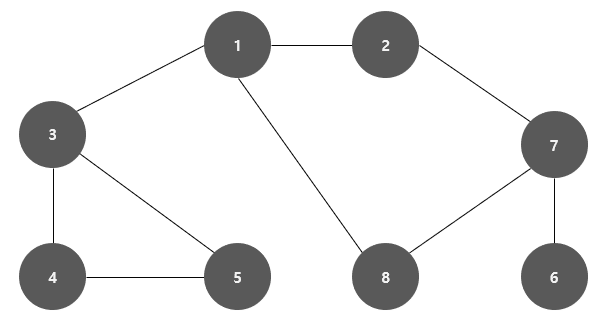
이와 같이 너비가 가까운 노드( 인접한 노드 )를 우선적으로 탐색하며 진행하는 그래프 탐색 방식을 너비 우선 탐색 ( BFS ) 라고 한다.

문제 분석

BFS를 진행하기 위해서 Queue자료 구조를 사용할 수 있다.

Queue를 사용하는 이유는 먼저 탐색한 노드를 먼저 빼내어 해당 노드와 인접한 노드를 탐색한다는 특성 때문이다. 이러한 FIFO특성에 맞는 자료 구조 중 가장 간단하고 빠른 Queue를 사용하는 것이다.

문제 해결 과정

1. 시작 점 1을 Queue에 넣고, 방문처리를 한다.
2. 1을 꺼내고 이와 인접한 2 3 8을 Queue에 넣고 방문 처리 한다.
3. Queue에서 2을 꺼내고 방문하지 않은 7번 노드를 방문 처리 후 Queue에 넣는다.
4. Queue에서 3을 꺼내고 방문하지 않은 4 5번 노드를 방문 처리 후 Queue에 넣는다.
5. Queue에서 더 이상 꺼낼 노드가 존재하지 않을 때 까지 반복한다.

구현

// BFS 함수 정의
// 연결 된 node의 정보를 담고 있는 graph, 시작 점, 방문 기록을 담고 있는 visited
void BFS(vector<vector<int>> graph, int start, vector<bool> visited)
{
	// 사용할 queue 정의
    queue<int> q;
    
    // 시작 점 queue에 삽입
    q.push(start);

	// 시작 점 방문 처리
	visited[start] = true;
    
    // queue가 빌 때까지 반복
    while(q.empty() == false)
    {
    	// 현재 노드를 뽑아오고 queue에서 제거
    	int node = q.front();
        q.pop();
        
        // 인접한 노드들을 탐색
        for(int i = 0; i < graph[node].size(); ++i)
        {
        	// 이미 방문한 node인지 체크
        	if(visited[graph[node][i]] == true)
            	continue;
                
            // 방문 처리 후 queue에 삽입
            visited[graph[node][i]] = true;
            q.push(graph[node][i]);
        }
    }
}

---

DFS

* 깊이 우선 탐색 ( Depth-First Search )

DFS는 깊이 우선 탐색으로 불리며 그래프에서 깊은 부분을 우선적으로 탐색한다.

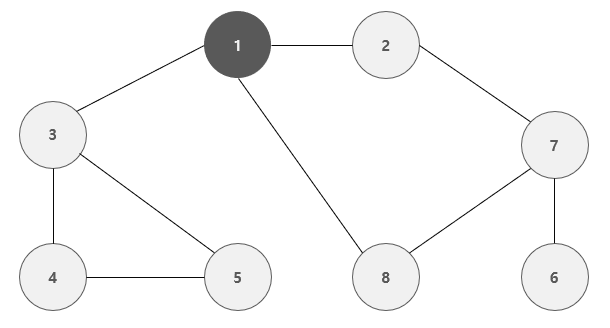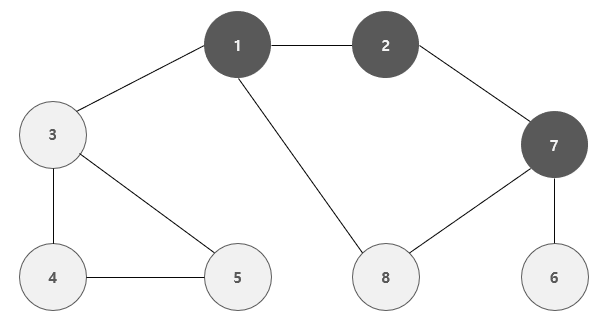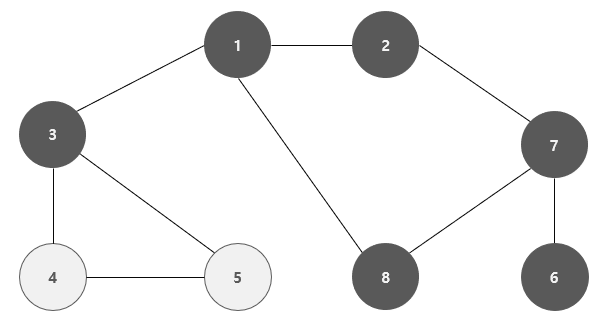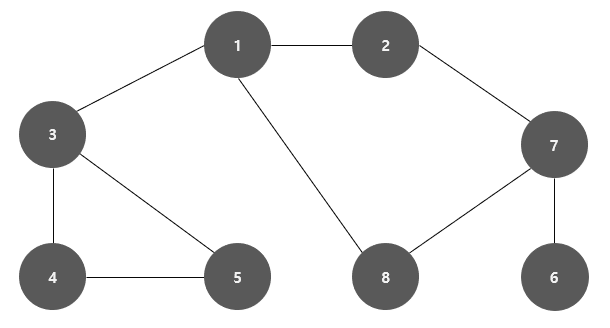
이와 같이 깊은 부분( 연결 된 간선을 모두 탐색 )을 우선적으로 탐색하며 진행하는 그래프 탐색 방식을 깊이 우선 탐색( DFS ) 라고 한다.

문제 분석

1) Stack 자료 구조 사용

마지막으로 방문한 노드와 연결 된 노드를 우선시하여 탐색을 진행하기에 LIFO구조를 사용하는 자료구조 중 가장 간결하고 빠른 Stack자료 구조를 사용할 수 있다.

2) 재귀함수 사용

재귀함수란 자기 자신을 다시 호출하는 함수를 말한다.

재귀 함수를 사용할 때는 종료조건을 정해준 후 해당 종료조건이 되기 전까지 함수를 무한히 실행하는데 이러한 조건으로 DFS를 해결하는데에 사용할 수 있다.

문제 해결 과정

1) Stack 자료 구조 사용

1. 시작점 1을 Stack에 넣고, 방문처리를 한다.
2. Stack 최상단 1번 노드와 미방문한 노드 중 가장 작은 2를 Stack에 넣고 방문처리한다.
3. Stack 최상단 2번 노드와 미방문한 노드( 7 )을 Stack에 넣고 방문처리 한다.
4. Stack 최상단 7번 노드와 미방문한 노드 중 가장 작은 6을 Stack에 넣고 방문처리한다.
5. Stack 최상단 6번 노드와 미방문한 노드가 없을 시에는 Stack에서 제거한다.
6. Stack 최상단 7번 노드와 미방문한 노드 ( 8 )을 Stack에 넣고 방문처리 한다.
7. 이와 같은 과정을 Stack에 값이 없을 때까지 반복한다.

2) 재귀함수 사용

1. 시작점 1번 노드와 미방문한 노드 중 가장 작은 2번 노드를 찾는다.
2. 2번 노드와 미방문한 노드( 7 )를 찾는다.
3. 7번 노드와 미방문한 노드 중 가장 작은 6번 노드를 찾는다.
4. 6번 노드와 미방문한 노드가 없을 경우 재귀를 종료한다.

구현

// Stack을 사용하는 DFS
// 연결 된 node의 정보를 담고 있는 graph, 시작 점, 방문 기록을 담고 있는 visited
void DFS_Stack(vector<vector<int>> graph, int start, vector<bool> visited)
{
	// 사용 할 Stack 정의
    Stack<int> st;
    
    // Stack에 시작 점 삽입
    st.push(start);
    
    // 시작 점 방문처리
    visited[start] = true;
    
    // Stack이 빌 때까지 반복
    while(st.empty() == false)
    {
    	// 현재 Stack에 최상위 값을 뽑고 Stack에서 제거
    	int node = st.top();
        st.pop();
        
        // 인접한 노드를 탐색
        for(int i = 0; i < graph[node].size(); ++i)
        {
        	// 인접한 노드를 찾아주기
        	int next = graph[node][i];
            
            // 이미 방문했는지 체크
            if(visited[next] == true)
            	continue;
            
            // 방문처리
            visited[next] = true;
            
            // pop을 해주었기 때문에 원본 node도 같이 Stack에 넣어준다.
            st.push(node);
            st.push(next);
            break;
        }
    }
}

//재귀를 사용하는 DFS
// 연결 된 node의 정보를 담고 있는 graph, 현재 노드, 방문 기록을 담고 있는 visited
void DFS_Recursive(vector<vector<int>> graph, int v, vector<bool> visited)
{
	// 현재 노드 방문처리
	visited[v] = true;
    
    // 인접한 노드 체크
    for(int i = 0; i < graph[v].size(); ++i)
    {
    	// 방문하지 않은 노드인지 체크
    	if(visited[graph[v][i]] == false)
        {
        	// 재귀 실행
        	DFS_Recursive(graph, i, visited);
        }
    }
}