[백준 1003번] 피보나치 함수

🔗알고리즘 문제

DP 문제의 기초라고 볼 수 있는 피보나치 관련 문제로 이제 이정도 DP 문제는 가볍게 풀 수 있게 되어 뿌듯했다 !

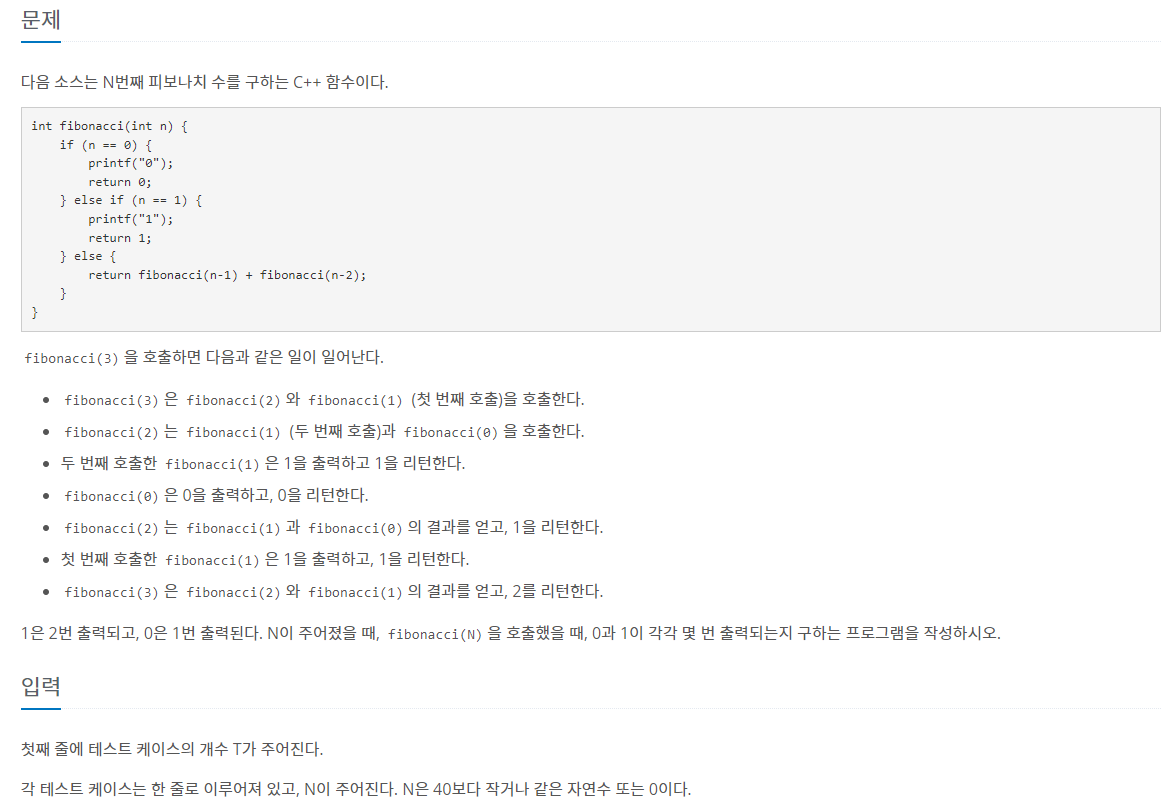
문제 분석

출처

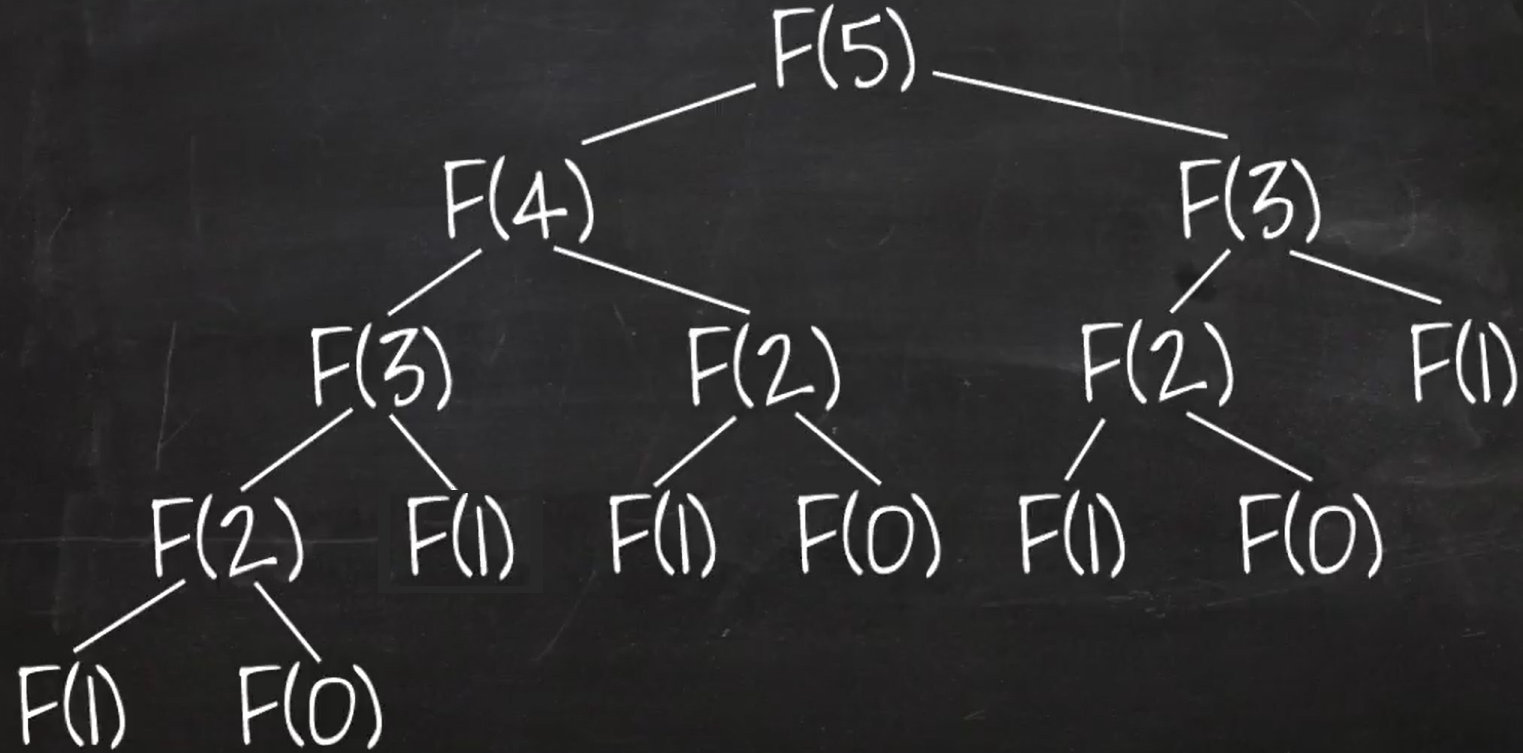
피보나치 함수는 위 이미지와 같이 재귀형식으로 진행된다.

이 문제는 간단히 말해서 Fibonacci(n)을 호출할 때 Fibonacci(0)과 Fibonacci(1)이 호출 되는 수를 구하는 문제이다.

위 이미지를 예시로 들면 Fibonacci(0)은 3번 Fibonacci(1)은 5번 호출되게 된다.

발상

재귀 형식을 유지한 채 호출될 때 마다 카운트를 해주는 방법도 있지만 그러기에는 호출되는 수가 너무 많아져 시간이 너무 오래걸리게 된다.

그래서 이 문제는 DP 알고리즘을 이용하여 해결해야 한다.

0과 1이 호출되는 횟수에서 한가지 규칙을 찾을 수 있는데 Fibonacci(n)에서 0과 1이 호출되는 횟수를 FiboCount(n)이라고 할 때 FiboCount(n) = FiboCount(n - 2) + FiboCount(n - 1)이라는 규칙을 알 수 있다.

알고리즘 설계

1. FiboCount(n) = FiboCount(n - 2) + FiboCount(n - 1) 이러한 규칙을 이용하여 최대 입력값인 40번째 피보나치까지의 값을 구해 dp배열에 담는다.
2. 입력받은 n의 fibonacci(0)이 호출되는 수와 fibonacci(1)이 호출되는 수를 출력한다.

코드

#include<iostream>

using namespace std;

int main(){
    int testCase;
    int n;

    int zero = 0, one = 0;

    pair<int, int> dp[41] = { {1, 0}, {0, 1} };

    for(int i = 2; i <= 40; i++)
        dp[i] = { dp[i - 1].first + dp[i - 2].first, dp[i - 1].second + dp[i - 2].second };

    cin >> testCase;

    while(testCase--){
        cin >> n;
        cout << dp[n].first << " " << dp[n].second << "\n";
    }
}