[백준 1238] 파티

🔗 알고리즘 문제

단순 n + 1번 다익스트라를 써서 해결한 문제. 먼가 찝찝해서 문제 평가를 읽어보니 역방향 다익스트라를 쓰는 아이디어로 해결할 수 있다고 한다. 나중에 다시 한번 풀어봐야겠다.

문제 분석

이 문제는 x라는 도착점이 주어질 때 시작점에서 x를 찍고 다시 시작점으로 돌아오는 최소거리가 가장 길 때에 거리를 구하는 문제이다.

예를 들어 예제에 나오는 그래프에서는

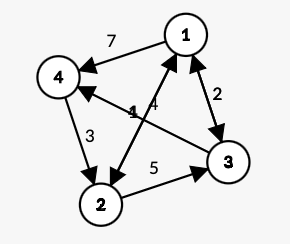
도착점이 2라고 할 때에, 시작점을 4으로 하면(4->2)(2->1->3->4) 최소거리가 10으로 가장 기므로 10이 정답이 된다.

발상 & 알고리즘 설계

이 문제는 다익스트라를 구현할 수 있다면 쉽게 해결할 수 있는 문제이다. 간선의 갯수가 적으므로 단순 n+1번 다익스트라를 돌려줘서 정답을 구해줘도 시간안에 해결할 수 있다.

한 가지 주의해야 할 점은 다시 돌아오는 것까지 최소 거리에 포함시켜야 하기에 도착점에서 시작점으로 한번 더 다익스트라를 진행해주어야 한다.

코드

#include<iostream>
#include<queue>
#include<climits>
#include<vector>
#include<algorithm>

using namespace std;

int n;
int m;
int x;

int answer = 0;
int temp = 0;

vector<pair<int, int>> v[1001] = {};
int check[1001] = {};

void dijkstra(int sv, int target){
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;
    fill(check, check + n + 1, INT_MAX);

    pq.emplace(0, sv);
    check[sv] = 0;

    while (!pq.empty()){
        int cur_i = pq.top().second;
        int cur_cost = pq.top().first;
        pq.pop();

        if(cur_i == target){
            break;
        }

        for(int i = 0; i < v[cur_i].size(); i++){
            int next_i = v[cur_i][i].first;
            int next_cost = cur_cost + v[cur_i][i].second;

            if(next_cost < check[next_i]){
                check[next_i] = next_cost;
                pq.emplace(next_cost, next_i);
            }
        }
    }

    temp += check[target];
    if(sv != x){
        dijkstra(x, sv);
    }
}

int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    cin >> n >> m >> x;

    for(int i = 0; i < m; i++){
        int from;
        int to;
        int cost;

        cin >> from >> to >> cost;

        v[from].emplace_back(to, cost);
    }

    for(int i = 1; i <= n; i++){
        if(x == i)
            continue;

        temp = 0;
        dijkstra(i, x);
        answer = max(answer, temp);
    }

    cout << answer;
}