[백준 20529] 가장 가까운 세 사람의 심리적 거리

🔗알고리즘 문제

비둘기집 원리라는 것을 처음 알게 된 문제이다. 로직 자체의 문제가 아닌 원리를 이용하여 시간초과를 해결해본 적은 처음이라 신기하였다.

문제 분석

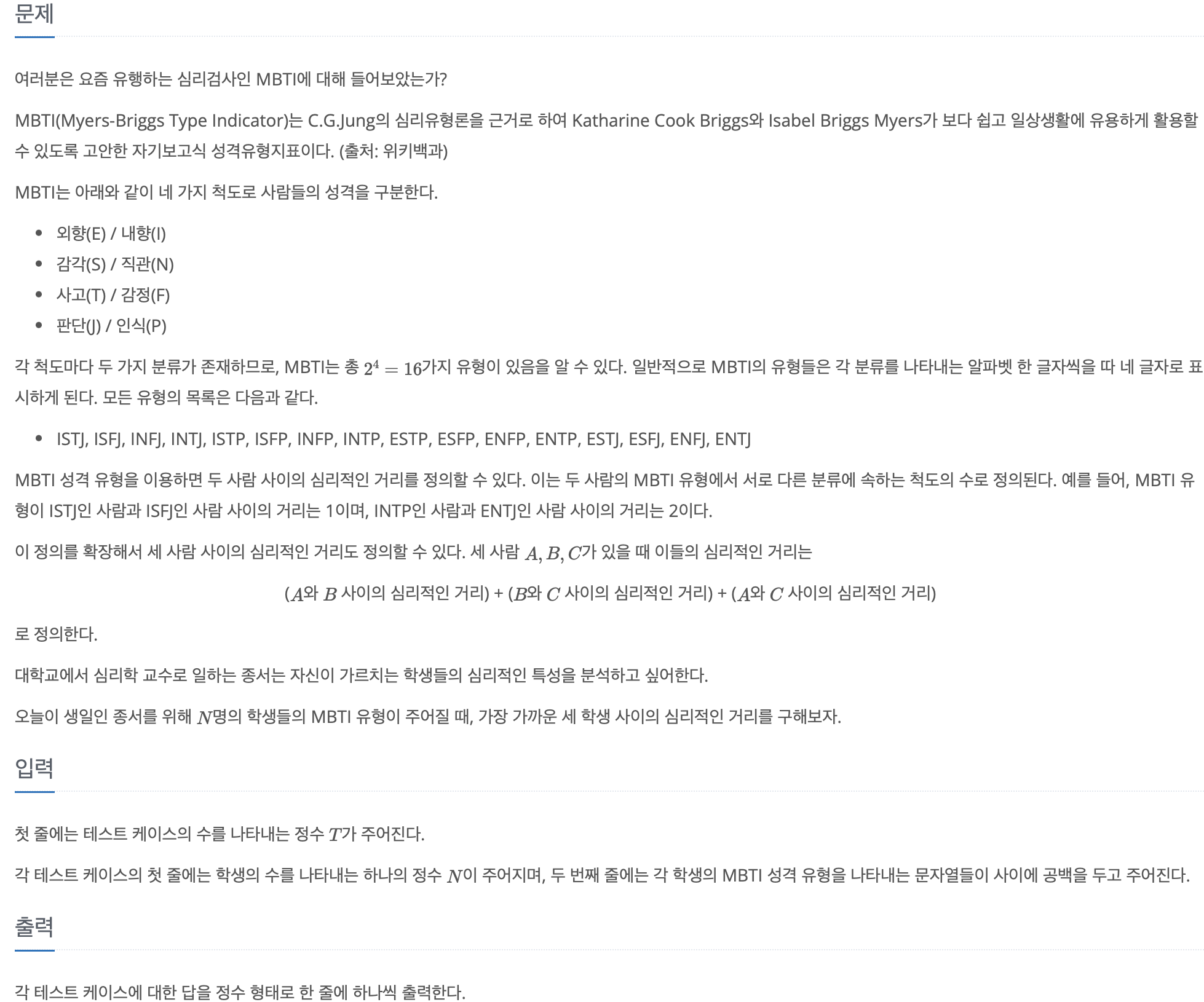
이 문제는 사람들의 mbti가 주어질 때 이 중 가장 가까운 세 사람의 심리적 거리를 알아내는 문제이다.

이 때 심리적 거리란 mbti 2개가 주어질 때 서로 다른 척도가 몇개인지를 나타내는 수이다.

 I	 N	 T	 P
 I	 N	 F	 P
(o)	(o)	(x)	(o)

=> 심리적 거리 = 1

발상 & 알고리즘 설계

처음에는 문제를 모든 사람들의 심리적 거리를 출력하는 문제라고 이해하였다.

for(int i = 0; i < n - 1; i++) {
    for(int j = i + 1; j < n; j++) {
    	val += CheckDistance(v[i], v[j]);
	}
}

하지만 문제에서 요구하는 바는 모든 사람들의 심리적 거리가 아닌 가장 가까운 세 사람의 심리적거리이다.

이를 해결하기 위해 고민하다 3중 for문을 통한 완전탐색으로 해결하기로 하였다.

for(int i = 0; i < n - 1; i++) {
    for(int j = i + 1; j < n; j++) {
        for(int k = j + 1; k < n; k++) {
            int dis = CheckDistance(v[i], v[j]) + CheckDistance(v[j], v[k]) + CheckDistance(v[i], v[k]);
        	val = min(val, dis);
    	}
	}
}

이러한 완전탐색을 통해 원하는 답을 잘 도출할 수 있지만 해당 문제에서 들어오는 최대 값의 수는 100,000개로 최악의 경우에서 3중 for문을 돌릴 경우 시간초과를 해결할 수 없었다.

여기서 비둘기집 원리를 생각해봐야하는데, mbti의 갯수는 총 16개로 n이 16보다 큰 경우 무조건 한쌍의 겹치는 mbti가 생기게 된다. 따라 n이 32보다 클 경우에는 무조건 겹치는 mbti가 3개가 생기게 된다.

이 경우 가장 가까운 세 사람의 심리적 거리는 0이 되므로 n이 32보다 큰 경우는 완전탐색을 진행하지 않고 바로 0을 출력해주었다.

코드

#include <iostream>
#include <vector>
#include <climits>

using namespace  std;

int CheckDistance(string &a, string &b){
    int val = 0;

    for(int i = 0; i < 4; i++){
        if(a[i] != b[i])
            ++val;
    }

    return val;
}

int  main()
{
    ios_base::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);

    int t;

    cin >> t;

    while(t--){
        int n;
        int val = INT_MAX;
        vector<string> v;

        cin >> n;

        for(int i = 0; i < n; i++){
            string mbti;
            cin >> mbti;
            v.push_back(mbti);
        }

        if(n > 32){
            cout << 0 << "\n";
        }
        else{

            for(int i = 0; i < n - 1; i++){
                for(int j = i + 1; j < n; j++){
                    for(int k = j + 1; k < n; k++){
                        int dis = CheckDistance(v[i], v[j]) + CheckDistance(v[j], v[k]) + CheckDistance(v[i], v[k]);
                        val = min(val, dis);
                    }
                }
            }

            cout << val << "\n";
        }
    }
}